
離散フーリエ変換(DFT)
井澤 裕司
1. フーリエ級数展開との関係
- はじめに、離散フーリエ変換(Discrete Fourier Transform; DFT)
とフーリエ級数展開との関係について
- 整理します。
- 離散フーリエ変換は、これまで述べてきたフーリエ級数展開において、
連続周期信号をサンプリングし、
- 離散周期信号に置き換えたものです。
- たとえば、整数を Nとしてサンプリング周期 T、 周期 NTの関数を
x*(t)
とおくと、デルタ関数 δ(t) を用いて、
- 次のように表すことができます。
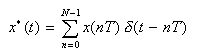
- ここで1周期分を考えれば
x*(t) は離散信号
x0 , x1, x2, ‥, xN-1
の関数となります。
- 次に、この関数1周期分について、これを複素フーリエ級数展開します。
- 小さな正数をεとして、以下の式が求められます。
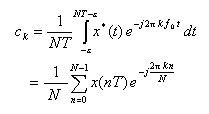
- このとき、デルタ関数 δ(t) の面積が T となることに注意して下さい。
- この理由については、下の[補足]で説明します。
- 次に、求めた複素フーリエ級数展開の係数 ck (k=0,1,2,
‥
,N-1) について、ck+N を求めます。
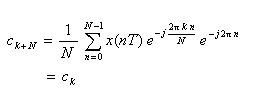
- これより、複素フーリエ級数展開の係数 ck
(k=0,1,2,‥,N-1) にも N の周期性があることがわかります。
- 一方、離散周期信号は、ck
を用いて次のように表わされます。
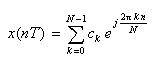
- これらより、離散フーリエ変換に関する以下の式が導かれます。
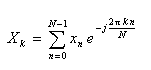
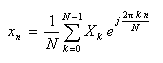
- ここで、離散フーリエ変換は離散周期信号と離散周期スペクトルを
結びつける関係式であることに注意して下さい。
[補足] δ関数について
- ここで、δ関数の性質について簡単に補足しましょう。
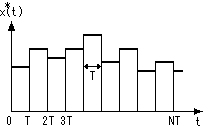
- 今、下の図に示すような周期NT
の関数 x*(t)
を考えます。
- 時間T毎に変化し、各々のTの中では一定の値をとるものとします。
- 変化する部分では、「ディリクレの条件」
を満たす必要がありますが、ここでは厳密な検討は行いません。
- このような関数 x*(t)
を、以下の図に示す関数 x(t)
と δ
0(t) を用いて表現することが可能です。
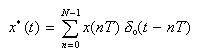
- x(t) は、t = NT における値
x(nT)
が与えられています。
- δ0(t)
は
t = 0~T で値 1 をとり、その他は 0 です。
- δ0(t)
の面積が T になることに注意して下さい。
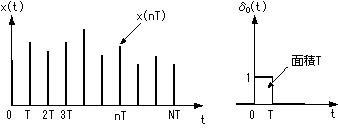
- 次に、 x*(t)
のような矩形状の関数を変形し、理想的なインパルス列の関数に近付けることを考えます。
- 上のδ関数δ
0(t)
の面積(T)を変化させずに、その幅Δを狭くしてゆきます。矩形の高さは T/Δとなり、
- 徐々に高くなってゆきます。
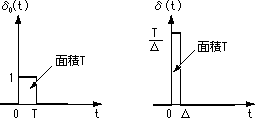
- このような極限が、理想的なδ関数となります。
- これより、δ関数を時間で積分すると、サンプリング周期 T の項が表れ、
前節の式が成立することがわかります。
2. 離散フーリエ変換の定義
- 離散フーリエ変換(DFT)の変換側の定義をもう一度示します。
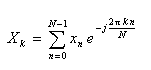
- 一方の逆変換側は、以下のようになります。
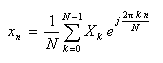
- ここで、単位円をN分割した点に相当する変数W を定義します。
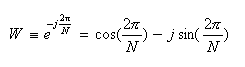
- この Wを用いて、離散フーリエ変換と逆変換の定義式を次のように書き改めることができます。
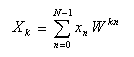
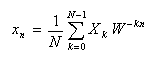
- ここで Wは回転子と呼び、以下の関係が成立します。
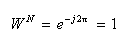
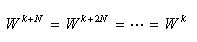
3. 離散フーリエ変換の性質
- ここで、離散フーリエ変換の性質について、N=8の場合を例に整理してみましょう。
- x0, x1,…,x7
の離散周期信号のスペクトルは離散周期スペクトルとなり、これを
X0, X1,…,X7
とします。
- これらの周期はいずれも 8 です。
- 下の図は、離散信号に対応するスペクトルを表示するツールです。
- x0, x1,…,x7
の信号成分には、それぞれ実部と虚部があり、図の下のバーを操作することにより、
- 自由に設定することができます。
- バーの上下にある(+) と (-) の部分をクリックして、様々な信号に対するスペクトルがどのような形に
- なるのか、調べて下さい。
- 例えば、入力信号がすべて実数のとき、スペクトルには対称性が現れます。
- それでは、次に左上の
「直流」
のボタンを押し、入力信号を一定値に設定して下さい。
- そのスペクトルをみると、X0のみある値を持ち、それ以外はすべて 0となることがわかります。
- 次に、
「1回転(+)」
のボタンを何回かクリックして下さい。
- このとき、信号は1周期の間に1回転するように変化します。
- 回転の向きは、原点から時間(+)の方向に見て時計方向を+(プラス)と定義しています。
- この信号の実部、あるいは虚部だけ観測すると、それぞれ正弦波に見えることになります。
- このときのスペクトルは、X1のみある値を持ち、それ以外はすべて0になります。
- すなわち X1は、複素数の信号に含まれる1回転する成分の大きさと位相を表しています。
- 「2回転(+)」
等のボタンも操作してみて下さい。
- これより、
X2, X3, X4,X5, X6, X7
は時計方向にそれぞれ2~7回転している信号の成分に対応している
- ことがわかります。
- それでは、質問です。反時計方向に1回転している信号成分はどのように表されるのでしょうか。
- 答は、「時計方向に7回転している成分に等しい」です。
- これらは、前章で述べたサンプリング定理や、Wの周期性から明らかです。
- 次の質問です。信号の虚数部を全て0にすると、そのスペクトルはどのようになるでしょうか?
- また、x0
について偶対称となる実信号の場合はどのようになるでしょうか。
4. マトリクスを用いた表現
- 上で定義した離散フーリエ変換を、マトリクス(行列)を用いて表現することが可能です。
- このような表現を用いることにより、変換と逆変換の関係をより直感的に理解することができます。
- マトリクスを用いると変換側は次のようになります。
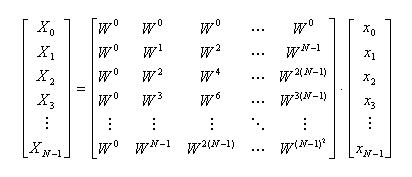
- ここで、信号 xn
(n=0,1,2,,N-1) とスペクトル Xn
(n=0,1,2,,N-1)をベクトルで、変換の関係式をマトリクス
- F
で表すと、次のようになります。
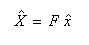
- 一方の逆変換は、次のように表せます。
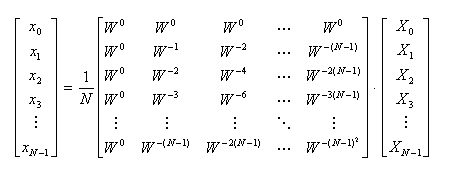
- この式もベクトルとマトリクスを用いて記述すると、次の式が得られます。ここで、バーは複素共役を
- 表しています。
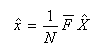
- ここで、離散フーリエ変換に対応するマトリクス
Fは正則であり、その逆行列は次のようになります。
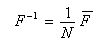
- この行列を、次の離散フーリエ変換を表す式の左からかけてみましょう。
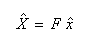
- 結果を下に示します。これより、逆変換の式が導かれました。
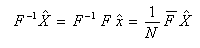
[確かめてみよう]
-回転成分に関する重ね合せの原理-
- ここで、離散フーリエ変換の物理的な意味について考えてみましょう。
- フーリエ級数展開では、「実数の周期関数はその整数倍の周期をもつ cos と sin の重ね合せで表すことができる」
- ということを学習しました。
- それでは、複素平面上の周期関数については、どのようになるのでしょうか?
- 答は、「複素平面上の回転運動成分の重ね合せ」 です。
- すなわち、整数倍の回転周期をもつ複数の回転運動成分の重ね合わせで表現することができます。
- 離散フーリエ変換についても、信号が離散的になるだけで、同じことが成立します。
- 下のツールを用いて、確認してみましょう。
- 図の下は、周期=8の離散周期信号の波形です。実部が縦軸、虚部は横軸で示されています。
- この信号をDFTして得られるスペクトルが、左下に表示されています。
- これらのスペクトル
X0, X1, X2,X3, X4, X5, X6,X7
は、1周期の間に 0, 1, 2, 3, 4, 5, 6, 7 回転する信号成分の
- 大きさと位相を表しています。
- 図の中央から上にかけて8種類の波形が表示されていますが、これらが各スペクトルに対応する回転成分です。
- この8種類の波形をベクトル的に加算すると、下に示した信号になります。
- スペクトルの値は自由に設定できますので、それらに対応する回転成分と、そのベクトル和がどのように変化
- するか、観察して下さい。
- なお、左上にいくつかの代表的な信号のボタンがありますが、それらをクリックすると対応する回転成分が
- 表示されます。ボタンの(複)とあるのは複素数(平面)、(実)、(虚)とあるのは実数と虚数です。
- 例えば、正弦波(実)をクリックして下さい。
- この正弦波の周期は1で実数の値をとりますが、2つの回転成分(1回と7回)の和で表されていることがわかります。
- 「時計方向に7回転」というのは、「反時計方向に1回転」に等価です。
- すなわち、これらの成分はそれぞれ回転方向が逆で、鏡のような位相関係(複素共役)をもつため、その和をとると
- 虚部は0となり、実数の信号になることがわかります。
-
[確かめてみよう] -回転成分の抽出 -
- それでは、ある方向に1周期の間に1回転する成分を検出するには、どのようにすればよいでしょうか?
- 「1周期の間に信号全体を逆方向に1回転させ、そのベクトル和を求める」というのが答です。
- そうすれば、検出したい成分は静止することになり、同じ方向を向くことになります。
- 他の回転成分は、ベクトル的に加算するとちょうど0となり、その影響は無視することが可能です。
- 以下、下の図を用いて具体的に確認してみましょう。
- はじめに、静止した成分について考えます。
- 右側に右を向いた8つのベクトルがあります。これが入力信号です。
- この信号を、時計方向に 0回転、1回転、2回転、…、7回転させながらベクトル的に加算します。
- その結果が左のベクトルで示されるスペクトルであり、
X0
が
→
の8倍となり、他はすべて 0 になります。
- 次に、右上の
(+)
のボタンを1回クリックし、反時計方向に1回転する入力信号を選択します。
- この場合、時計方向に1回転させる
X1
の項が
→
の8倍となり、他はすべて 0になります。
- ボタンの
(+)
と
(-)
を操作して、様々な入力信号について、
そのスペクトルがどのようになるか確認して下さい。
[確かめてみよう] -離散フーリエ変換 (N=4)の場合-
- ここで、離散フーリエ変換について、N=4の場合を例にとり、確かめてみましょう。
- 変換側は次のようになります。
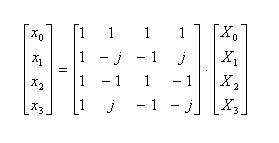
- 一方の逆変換は、以下の通りです。
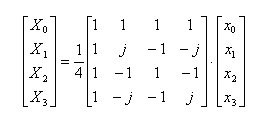
- ここで、1,1,0,0
という信号について、そのスペクトルを計算すると、次のようになります。
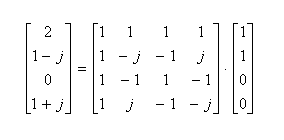
- このスペクトルを逆変換の式に代入します。結果は以下の通りで、もとの信号が得られました。
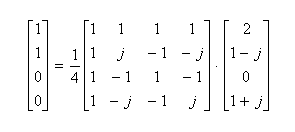
- 実数の信号の場合、スペクトルは第3項に対して共役複素数の関係になっていることがわかります。
5. まとめ
- 本章では、離散フーリエ変換について学習しました。
- この変換式から明らかなように、これらの変換にはある対称性が存在します。この性質を用いて乗算数を飛躍的に
- 少なくする方法があります。これがいわゆる「高速フーリエ変換(FFT)」です。次章では、その具体的な実現手法
- について、学習します。
-
-
⇒ ディジタル信号処理(基礎編)に戻る

