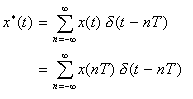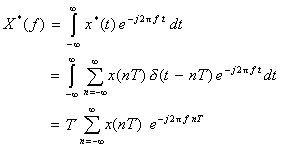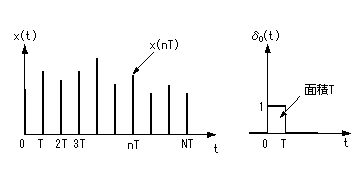サンプリングとそのスペクトル
井澤 裕司
1. サンプリング信号のスペクトル
- サンプリング(標本化)とそのスペクトルの関係について考えてみましょう。
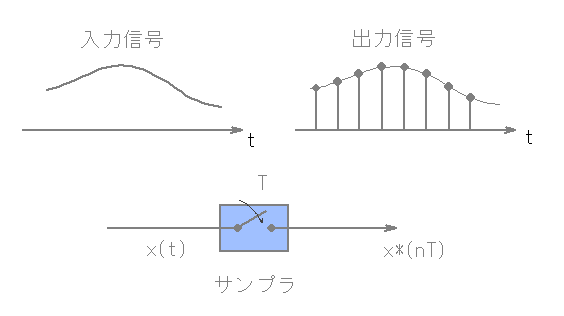
- サンプリングは、下の図に示すように、連続信号
x(t)
を時間
T
毎に離散信号
‥ ,x(-T), x(0), x(T), x(2T), ‥
に
- 変換する操作です。
- なお、サンプリング周波数は
fs = 1/T
で表わされます。
2. サンプリング定理について
- 連続するアナログ信号をサンプリングして離散的な信号に変換する場合に、注意しなければならない条件があります。
- はじめのディジタル信号処理の基本構成のところでも述べましたように、この条件を満たさないと、サンプリングした信号に、
- 本来のアナログ信号には含まれていない特有の歪(折り返し歪)が発生し、様々な悪影響をもたらすことがあります。
- 注意しなければならないことは、ある周波数でサンプリングした離散信号をもとに、これを間引いて、さらに低い
- サンプリング周波数の離散信号を求める場合にも、同様の歪を発生させる点です。
- このような条件を定式化したのが、
シャノン・染谷による「サンプリング定理
」です。
- その物理的な意味を考えてみましょう。
- 下の図は時計を表しています。左側はアナログ時計、右はディジタル時計です。
- ディジタルとは言っても、アナログ時計を一定の間隔で発光するストロボ光のもとで、観察しているものと考えてください。
- あるいは、一定の間隔で撮影した写真を眺めていると考えても結構です。
- アナログの時計は1秒間に1回転しています。
- 右側のボタンは、発光するストロボの周波数(あるいは周期)を調整するためのものです。
- 今、ボタンの+を何度も押して、周波数を例えば5Hzに上げてみましょう。
- 右側のディジタル時計は少し遅れはしますが、時計方向に正常に回転していることがわかります。
- 今度は、ボタンの-を押して、サンプリング周波数を 2.5Hz に下げてみます。
- まだ、時計方向に回転しています。
- 次は、2.08Hzです。まだ、なんとか時計方向であることが判ります。
- 見方により、逆方向に回転しているように感じられるかもしれませんが、角度の少ない方向に回転すると考えれば、
- 時計方向です。
- ところが、サンプリング周波数をアナログ時計の周波数の2倍、すなわち 2Hz にすると、ディジタル時計の針は上と下を
- 行き来して、回転する方向が判別できなくなります。
- さらに、周波数を下げてみましょう。例えば 1.25Hzにすると、ディジタル時計は反時計方向に回転して見えます。
- そのときの回転数は1/4となり、周期は4秒に相当します。
- それでは、サンプリング周波数をアナログ時計の周波数に等しい 1Hz にすると、どのようになるでしょうか?
- 答えは、もうおわかりですね。静止しているように見えます。
- 以上の現象をまとめます。
- 時計方向に回転していることがわかるぎりぎりの周波数は 2Hz で、それ以下では正しい観測結果が得られないという
- ことになります。
- これより、以下のサンプリング定理が導かれます。
- 「連続信号をサンプリングして離散信号に変換するとき、その信号に含まれる最高の周波数の2倍以上の周波数
- でサンプリングすれば、完全に復元することができる。」
3. サンプリング信号のスペクトル
- いま、ディラックのデルタ関数
δ(t)
を用いると、サンプリングされた離散信号
x*(t)
を次のように表すことができます。
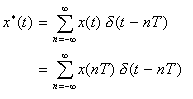
- 上で定義した
x*(t)
のスペクトルを求めるため、この式を
フーリエ変換
します。
- デルタ関数
(
δ(t)
)は
t = 0
における理想的なインパルスであり、その面積は
T
です。(その理由については、次の
[
補足]
で説明します。)
- このとき
、サンプリングした信号のスペクトル
X*(f)
は、次式のようになります。
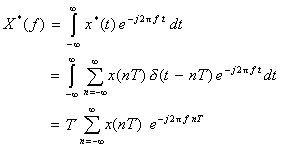
[補足] δ関数について
- ここで、δ関数の性質について簡単に補足しましょう。
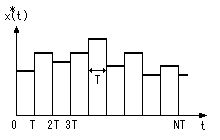
- 下の図に示すような周期
NT
の周期関数
*(t)
を考えます。
- この関数はサンプリング周期
T
毎に変化し、各々の
T
の中では一定の値をとるものとします。
- 変化する部分については
「ディリクレの条件」
を満たす必要がありますが、ここでは厳密な検討は行いません。
- このような関数
x*(t)
を下の図に示す関数
x(t)
と
δ0(t)
を用いて表現することができます。
- δ0(t)
は
t = 0~T
で値
1
をとり、その他は
0
です。
- δ0(t)
の面積が
T
になることに注意して下さい。
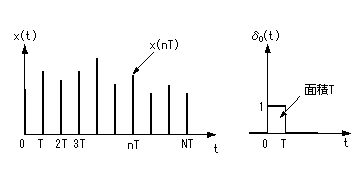
- 次に、矩形状の関数
x*(t)
を変形し、理想的なインパルス列
に近付けることを考えます。
- 上の関数
δ
0(t) の面積(
T
)を変化させずに、その幅
Δ
を狭くしてゆきます。
- このとき、矩形の高さは
T/Δ
となり、徐々に高くなってゆきます。
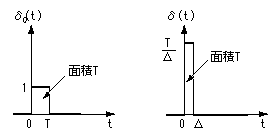
- このような極限が、理想的な
δ関数
となります。
- これより、
δ関数
を時間で積分するとサンプリング周期
T
の項が現れることがわかります。
4. フーリエ級数展開との関係
- 信号とスペクトルの項で述べましたように、サンプリングはフーリエ級数展開と双対な関係にあります。
- 以下、具体的に説明しましょう。
- 下に複素フーリエ級数展開の式を示します。
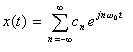
- この式と、上で求めた
X*(f)
の式を比較してみましょう。
- サンプリングの連続スペクトル
X*(f)/T
と、複素フーリエ級数展開の連続信号
x(t)
が対応しています。
- Σ
の
n =-∞, ‥,∞
は同じ形式です。
- 自然対数 e の指数部の対応する項を整理すると、次の表のようになります。
| サンプリング |
X*(f)/T |
x(nT) |
-2πf ( = -ω) |
T |
| 複素フーリエ級数展開 |
x(t) |
Cn |
t |
ω0 |
- サンプリングの離散信号
x(nT)
とフーリエ級数展開の係数(離散スペクトル)
C
n
が対応します。
- 同様に、連続周波数(
-2πf
)と連続時間(
t
)、離散時間(
T
)と離散(角)周波数(
ω
0
)が対応します。
- このように、サンプリングと、複素フーリエ級数展開は時間と周波数を入れ替えた関係にあり、これらは
- 双対な関係
にあると言います。
5. スペクトルの周期性について
- サンプリングした信号のスペクトルには、周期性があります。
- 以下、具体的に検討してみましょう。
- 任意の整数を
k
として
X*(f+k/T)
を計算します。
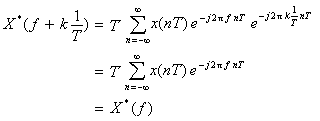
- これより、サンプリング(標本化)した信号のスペクトルは周期信号であり、その周期は
1/T
になることが分かります。
- すなわち、サンプリング(標本化)した
離散非周期信号
は、
連続周期スペクトル
をもちます。
[確かめてみよう] -サンプリングとそのスペクトル-
- サンプリングした信号とスペクトルの関係を確認してみましょう。
- 下の図は、25のサンプリングされた離散信号について、その連続スペクトルを示したものです。
- これらの25個の信号以外は値0であり、周期信号ではない(すなわち、非周期信号である)ことに注意して下さい。
- (ちなみに離散周期信号については、離散フーリエ変換(DFT)の項で解説します。)
- 例えば、左上の「正弦波」のボタンをクリックして下さい。
- そのスペクトルは、-fs/2~fs/2を周期とする連続スペクトルになります。
- ボタンを何度か押し続けると、信号の位相がシフトします。
- 25個の信号のなかで、中央に位置する信号は「S12」です。この中点について左右対称形となるとき、
- スペクトルの実部は全て0 となり、虚部は中央の周波数 0、すなわち直流について奇対称となります。
- 一方、信号が中央について偶対称となるとき、そのスペクトルの虚部は
0 となり、実部は周波数=0について
偶対称となります。
- 信号を切り替えたり、位相をシフトすることにより、そのスペクトルがどのような値になるか、理解して下さい。
6. まとめ
- 本章では、サンプリングとそのスペクトルの関係について検討しました。
- このサンプリングは、離散非周期信号を連続周期スペクトルに関係付けるものであり、先に述べたフーリエ級数展開とは、
- 互いに双対関係にあることを示しました。
-
⇒ ディジタル信号処理(基礎編)に戻る