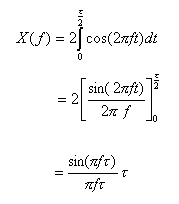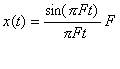フーリエ変換とその性質
井澤 裕司
1. はじめに
- 本章では、フーリエ変換について学習します。
- フーリエ級数展開のある極限をとると、フーリエ変換が得られます。
- このフーリエ変換は、変換と逆変換が共に積分の形になっており、ある意味では分かり難いと感じられる
- 方もいるのではないでしょうか?
- このような場合は、フーリエ級数展開をもう一度よく復習し、その極限を考えてみて下さい。
- あるいは、この後解説する離散フーリエ変換を先に学習するのも、ひとつの方法です。
- これらの方が、変換と逆変換の関係が直感的に理解しやすいためです。
- それでは、フーリエ変換の変換・逆変換の関係を導きましょう。
- はじめに、複素フーリエ級数展開について簡単に復習します。
- この複素フーリエ級数展開では、周期
T0
をもつ連続信号を対象にします。
- この複素スペクトル
cn
は離散スペクトルとなり、その間隔は
1/T0
です。
- 例えば、周期
T0
を2倍にすると、その離散スペクトルの間隔も1/2になります。
- ここで、周期を無限に大きくすると、そのスペクトルの間隔は 0 となり、
離散スペクトルは連続スペクトルに
- 変化します。
- 以下、具体的に説明しましょう。
2. フーリエ変換とは
- 複素係数
cn
と周期
T0
の積を
X(jnω0)
とおきます。
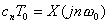
-
cn
を次元のない量とすると、
X(jnω0)
は時間の次元を持つことに注意して下さい。
- この式を用いて、前章で述べた複素フーリエ級数展開の式を書き改めます。
-
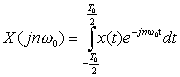
- ここで、
T0 →∞
すなわち
ω0 →0
の極限で、離散的な角周波数
nω0
(n = -∞,‥,-1,0,1,2,‥,∞)
- は、連続的な角周波数
ω
に置き換えられるものとします。
- このとき、次の変換式が成立します。
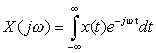 (フーリエ変換)
(フーリエ変換)
- 次に、逆変換について求めます。
- Δω=ω0
とおくと、フーリエ級数展開の式は、
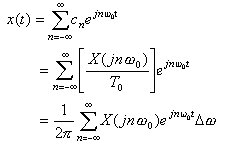
- となり、
ω0 →0
の極限では、
-
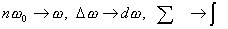
- に置き換えられるので、最終的に、
-
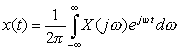 (フーリエ逆変換)
(フーリエ逆変換)
- が得られます。
[フーリエ変換と逆変換] (まとめ)
- x(t)がディリクレの条件を満たし、絶対可積分のとき、次の関係が成立します。
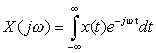 フーリエ変換
フーリエ変換-
-
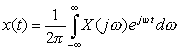 フーリエ逆変換
フーリエ逆変換
- あるいは、周波数 f = ω/2πを用いて次のように表現することもあります。
-
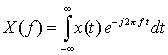 フーリエ変換
フーリエ変換
-
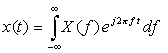 フーリエ逆変換
フーリエ逆変換
[確かめてみよう] -フーリエ級数展開からフーリエ変換へ-
- 複素フーリエ級数展開の周期
T0
を無限大にすると、離散スペクトル
cn
の間隔は無限小となり、
- その極限で連続スペクトルになります。
- この関係を下の図に示します。
- この画面上に表示できる解像度の限界がありますので、
スペクトルの間隔が一旦止まっているように
- 見えますが、実際には滑らかに変化しています。
- 繰り返しますが、フーリエ変換では、
連続非周期信号が同じ連続非周期スペクトルに変換されることに
- 注意して下さい。
4. フーリエ変換対について
- 次に、フーリエ変換と逆変換の双対性について補足しましょう。
- 2つ目の定義では、x(t)と X(f) を入れ替えると、自然対数 e
のマイナスの有無の違いはあるものの、
- 後は同じ形をしています。このマイナスは、回転の方向が違うことに相当し、
共役複素数で表されます。
- このとき、信号とスペクトルは双対の関係にあると言います。
- 以下、具体的な例を用いて説明しましょう。
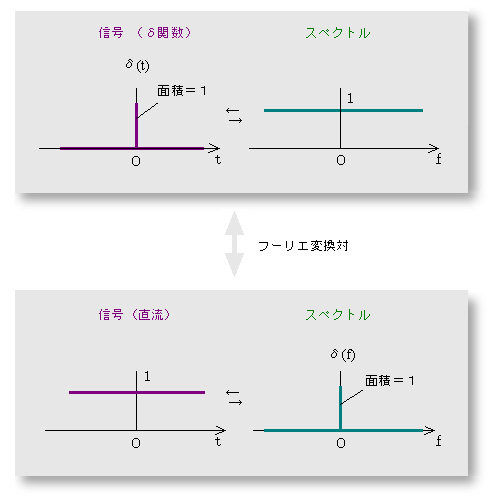
- (例1)δ(デルタ)関数の場合
- 信号がδ関数 [δ(t)]の場合、
そのスペクトルは周波数にかかわらず1という値になります。
- このδ関数は、ディラックにより定義される理想的なインパルス関数であり、
その面積は1です。
- 一方、信号が時間にかかわらず1のとき、そのスペクトルは図のようにδ関数
[δ(f)] になります。
- すなわち、時間 tに関する信号と、周波数 f
に関するスペクトルを入れ替えた関係が成立しています。
- (例2)方形波の場合
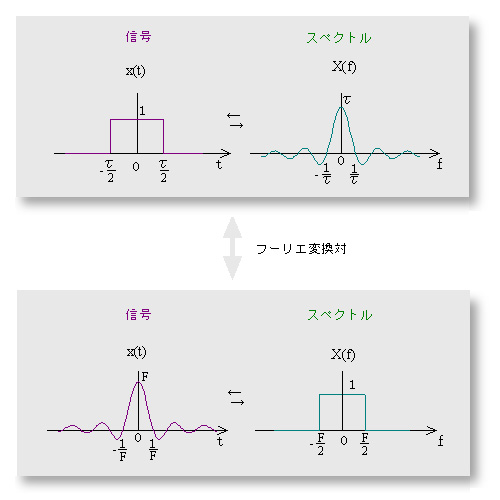
- 下に方形波の例を示します。
- 信号が図のような方形波のとき、そのスペクトルは図のようなsinc関数になります。
- この関数は以下にしめすように sin(x)/x で表される関数であり、x = 0 で 1
という値をもちます。
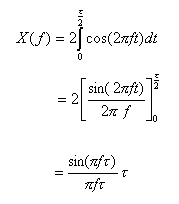
- 一方、信号が次のようなsinc関数のとき、そのスペクトルは方形波になります。
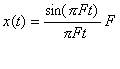
5. フーリエ変換の性質
- フーリエ変換の性質について、整理します。
- (1) 線形性
- 任意の実数 a, b について、以下の関係が成立します。
- この線形性は、フーリエ解析の最も重要な性質です。
- しっかり、頭に入れておきましょう。
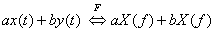
- (2) 実信号のフーリエ変換
- ■ x(t) が実数のとき
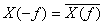
- これは、前章の複素フーリエ級数展開の項をみれば、理解できると思います。
- ■ x(t) が実数かつ偶対称のとき、X(f) も実数かつ偶対称となる。
- x(t) が偶対称のとき、スペクトルの虚数部は0 になるので明らかです。
- (3) Parseval の公式
-
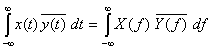
- ここで、x(t) = y(t) のとき
-
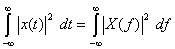
- [証明]
左辺
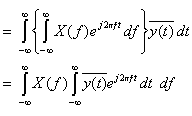
= 右辺
6. まとめ
- フーリエ変換とその性質について、学習しました。
- この性質の大部分は、後に説明する離散フーリエ変換(DFT)でも成立します。
- これらを比較し、その違いに注目して整理してみると、
スペクトル解析の体系的な理解に役立つと思います。
-
⇒ ディジタル信号処理(基礎編)に戻る
-


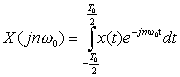
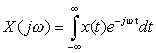 (フーリエ変換)
(フーリエ変換)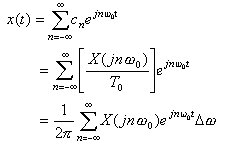
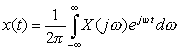 (フーリエ逆変換)
(フーリエ逆変換)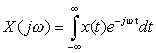 フーリエ変換
フーリエ変換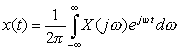 フーリエ逆変換
フーリエ逆変換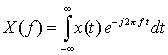 フーリエ変換
フーリエ変換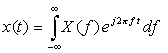 フーリエ逆変換
フーリエ逆変換