信号処理とスペクトル

　　　井澤　裕司　　

1.　スペクトルとは何か？

「スペクトル」 という言葉を聞いて何を連想されるでしょうか？

フーリエ変換 等の用語がまず頭に浮かんだ方は、以下を読み飛ばして項目3に進んで下さい。

一般には、プリズムを用いて白色光を赤黄‥紫の7色に分解した虹のようなものを
思い浮かべるのではないでしょうか。

光は一種の波です。赤い光の波長は長く、紫の光は逆に短くなっています。
周波数（振動数）は波長の逆数ですので、赤は低い周波数、紫は高い周波数の光に相当します。

白色光には、様々な波長（周波数）の光が含まれており、プリズムによりそれぞれの成分に分解
されます。この周波数（あるいは波長）に対する各成分の分布を スペクトル と言います。

光だけでなく波動で表現できる物理量すべてに、このスペクトルという概念を適用することが可能です。
例えば、電波や電気信号だけでなく、為替の相場等にも適用できます。

2.　スペクトルの利用例

次に、 「スペクトルを用いると、どのようなことができるのか？」 について考えてみましょう。

例えば、人間の音声信号を分析して、男女や個人の違いを識別することができます。
ディジタルオシロスコープを用いて時間の関数として記録し、その波形を細かく観察しても、
それらを識別することはそれほど簡単ではありません。
しかし、 スペクトルアナライザ という装置を用いて、周波数の分布を調べることにより、
時間軸では判別できなかった周波数の分布の違いを検出することが可能です。

すなわち信号のスペクトルを分析して、その信号源を同定したり、 特徴パラメータ を抽出して パターン認識 に利用
する方法があります。

次に、記録や通信への利用法があります。
入力信号をスペクトルに変換すると、特定の周波数に偏っていることがあります。
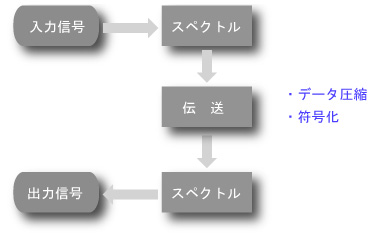
このような場合、信号を直接伝送するより、送信側でそのスペクトルを求めて伝送し、
受信側で送られてきたスペクトルからもとの信号を復元した方が、効率的であることが多いのです。

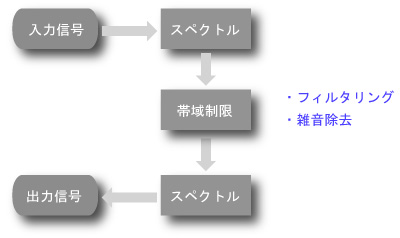
入力信号の中から、特定の成分を取り出したり、雑音のみを除去する場合に、
スペクトルが利用されます。

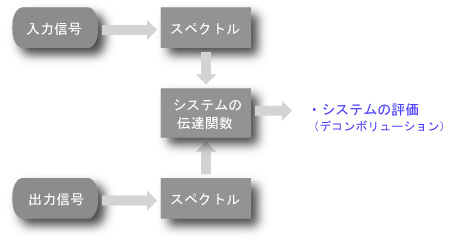
ある未知のシステムの特性を明らかにする場合、既知の入力に対する出力を求める手法が用いられます。
これらを直接時間の関数として計算するより、入力と出力のスペクトル（システムの伝達関数）を求め、
この商を計算する方が効率的です。この手法を、 デコンボリュ−ション と呼びます。
詳しくは、線形システムの伝達関数（畳み込み積分）の項で解説します。

以上、スペクトルの利用法についていくつかの事例を紹介しましたが、これ以外にも多くの利用方法が存在します。
それらについては、各自調べてみて下さい。

3.　（周期／非周期）と（連続／離散）の相互関係

前にも述べたように、信号には連続（アナログ）信号と離散（ディジタル）信号があります。
また、周期性がある信号と、周期性がない信号があります。

一方、スペクトルにも、 連続スペクトル と 離散スペクトル 、 周期スペクトル と 非周期スペクトル があります。
これらは独立ではなく、ある相互関係が存在します。
詳しくは対応する項目で説明しますが、以下のような関係があります。
少し乱暴な言い方になるかもしれませんが、離散信号は有限です。
有限なものをある規則により変換した結果は有限であり、それらが連続関数の形をとる場合は、
何らかの形で繰り返し（周期関数）の形をとります。

上の法則を組み合わせると、以下のようになります。

連続周期信号 は 離散非周期スペクトル をもち、これらの関係を記述するのが 「フーリエ級数展開」 です。

連続非周期信号 は 連続非周期スペクトル になり、これらの関係は一般の 「フーリエ変換」 で記述されます。

離散周期信号 は 離散周期スペクトル であり、 「離散フーリエ変換」 に対応します。

それでは、残る組み合せ、 離散非周期信号 と 連続周期スペクトル を関係付けるのは、何でしょうか？
答えは、 「サンプリング（標本化）」 という操作です。

以上の関係を整理すると、次の図のようになります。

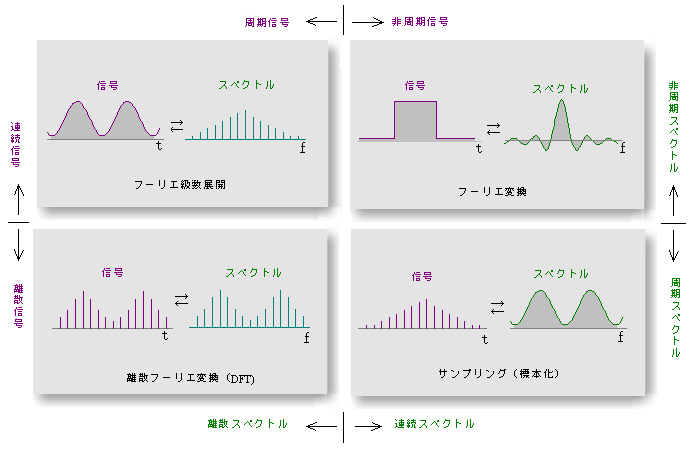
　　図　（周期／非周期）と（連続／離散）の相互関係

4.　まとめ

信号処理とスペクトルの関係を整理し、以下の４つの処理の相互関係について述べました。
これらを独立に勉強するのでなく、それらの 相互関係 に十分注意を払いながら、学習を進めることが重要です。

なお、コンピュータ等を用いて信号処理する場合、当然離散的な信号を扱うことになります。
すなわち対象とする信号は、連続的な信号ではなく、 サンプリング（標本化）された離散信号 です。

また、データの時間長も無限に長くすることは不可能ですし、スペクトルを限りなく細かく計算しても、
「不確定性の原理」 により、意味のある結果が得られるわけではありません。
すなわち、スペクトルはある程度の周波数間隔で計算すれば、それより細かい部分ついては内挿することにより
推定することができるのです。

このように コンピュータでの扱い は、信号も 離散信号 、スペクトルも 離散スペクトル になります。
ただし、いずれも暗黙のうちに周期性が仮定されているということに注意して下さい。
この周期は十分長いので実際上問題は生じないということです。

　 ⇒　ディジタル信号処理（基礎編）に戻る