
ラプラス変換
井澤 裕司
1. はじめに
- 4章では,
フーリエ変換
について学習しました.
- 本章では,これを過渡現象の解析にも利用できるように拡張した
ラプラス変換
について解説します.
- この
ラプラス変換
により,線形システムの応答や微分方程式の解を比較的簡単な
四則演算
により求めることができます.
- ラプラス変換
では,積分記号で表される操作が、
変換
と
逆変換
で基本的に異なっており,
- フーリエ変換
に比べ物理的なイメージを掴むことが難しいと言われていますが,
- ここではその本質的な意味が直観的に把握できるようイメージ化を試みます.
2. ラプラス変換とは
- 本節では
ラプラス変換
と
逆ラプラス変換
の定義を示し,いくつかの
例題
を通して
- その
物理的なイメージ
を探ります.
2.1 定義(狭義)
- 時間
t ≧ 0
で定義された関数
f (t)
について,
- 以下に示す積分
F (s)
を
f (t)
の
ラプラス変換
といいます.
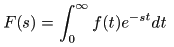
- ここで,
t
は実数,
s
は複素数であり,
e-s t
を
収束因子
,
- f (t)
を
原関数
,
F (s)
を
像関数
と呼びます.
- なお,原関数
f (t)
と,像関数
F (s)
の関係を,以下のように表現することがあります.
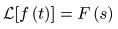
- 一般に
F (s)
は
s
の値により
収束
したり
発散
したりしますが,
- 例えば
s
の実部
Re (s) = σ
が
σ > σc
の条件で
収束するとき,この
σc
の上限を
収束座標
,
- σ > σc
を満たす
s
の領域を
収束域
と呼びます.
- なお,後ほど詳しく説明しますが,狭義の
F (s)
は
変数
の
jω
を
σ
の方向に拡張した一種の
スペクトル
であり,
- その
次元
は
[f (t)の次元×時間]
となります.
- 一方,
逆ラプラス変換
の定義は次のようになります.
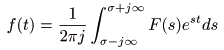
- ここで,
s = σ + j ω
であり,
t < 0
で
f (t) = 0
とします.
- また,
逆ラプラス変換
を以下のように表すことがあります.
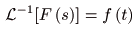
- なお,
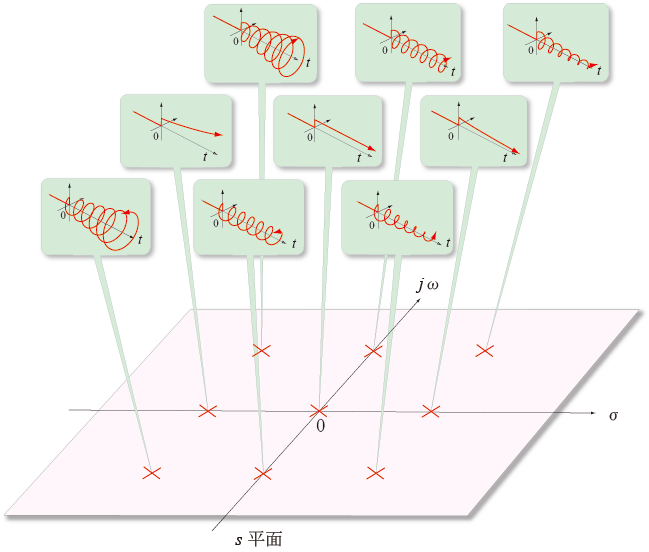
s = σ + j ω
として,
s平面
における
収束因子
e-s t
を図示すると,
- その半径が
指数関数
で発散したり,減衰する
コイルばね
のような形状になります.
[例題1] 単位ステップ関数 u (t) のラプラス変換
- 単位ステップ関数
u (t)
は,
t < 0
のとき
u (t) = 0
,
t > 0
のとき
u (t) = 1
となる関数です.
- この
関数
を
ラプラス変換
すると,以下のようになります.
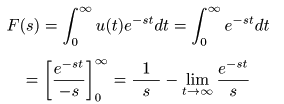
- ここで,複素変数
s
の実部が正,すなわち
Re(s) = σ > 0
のとき,上式の第2項が
0
となり,
- 以下の式が導かれます.
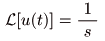
- すなわち,
u (t)
の
ラプラス変換
は,
σ > 0
の収束域で
F (s) = 1/s
という
複素関数
になります.
[例題2] 指数関数 f (t) = e-αt のラプラス変換
- 次に
α
を正の実数として,
指数関数
f (t) = e-αt
の
ラプラス変換
を求めてみましょう.
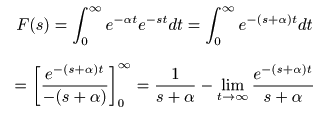
- ここで,複素変数
s
の実部
Re (s)
を
σ
として
σ > -α
のとき,上式の第2項が
0
となり,
- 以下の式が導かれます.
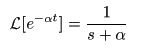
- すなわち,
指数関数
の
ラプラス変換
は,
σ > -α
の収束域で
F (s) = 1 / (s+α)
になります.
- ここで
α = 0
とおくと,
例題1
で示した
単位ステップ関数
の結果に一致します.
[例題3] 三角関数 f (t) = cos (ωt) のラプラス変換
- 次に
ω
を正の実数として,
三角関数
f (t) = cos (ωt)
の
ラプラス変換
を求めます.
- 後ほど詳しく説明しますが,
指数関数
と
三角関数
を結び付ける
オイラーの公式
を以下に示します.
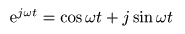
- ここで
ω
に
-ω
を代入すると,次式が得られます.
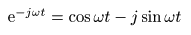
- 上の2 式を加算し,2 で割ると,
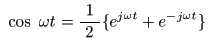
- が得られます.
- これより,
ラプラス変換
の
線形則
を適用して,
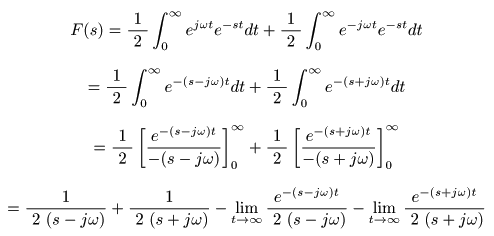
- ここで,複素変数
s
の実部
Re (s)
を
σ
として
σ > 0
のとき,上式の第3項,第4項が
0
となり,
- 以下の式が導かれます.
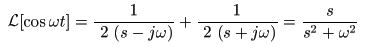
- すなわち,
三角関数
cos (ωt)
の
ラプラス変換
は,
σ > 0
の収束域で
F (s) = s / (s2+ω2 )
になります.
- ここで,
ω = 0
とおくと
F (s) = 1 / s
となり,
例題1
の結果に一致します.
[例題4] 三角関数 f (t) = sin (ωt) のラプラス変換
- 例題3
と同様に
ω
を正の実数として,
三角関数
f (t) = sin (ωt)
の
ラプラス変換
を求めます.
- オイラーの公式
から得られる2式に減算を適用し,
2 j
で割ると,
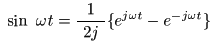
- が得られます.これより,
cos
の場合と同様にして,
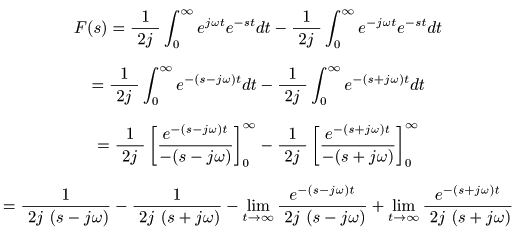
- ここで,複素変数
s
の実部
Re (s)
を
σ
として
σ > 0
のとき,上式の第3項,第4項が
0
となり,
- 以下の式が導かれます.
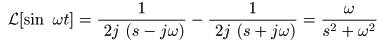
- すなわち,
三角関数
sin (ωt)
の
ラプラス変換
は,
σ > 0
の収束域で
F (s) = ω / (s2+ω2 )
になります.
[例題5] 減衰振動関数 f (t) = e-αt cos (ωt) のラプラス変換
- 次に
α
と
ω
を正の実数として,
関数
f (t) = e-αt cos (ωt)
の
ラプラス変換
を求めます.
- オイラーの公式
と
指数関数
の性質から,以下の式が得られます.
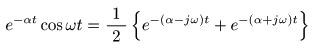
- これより,
ラプラス変換
の
線形則
を適用して,
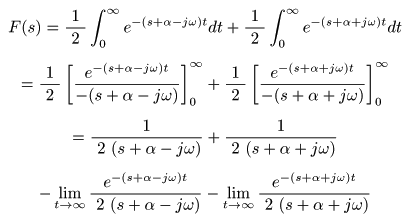
- ここで,複素変数
s
の実部
Re (s) = σ
が
σ > -α
のとき,上式の第3項,第4項が
0
となり,
- 以下の式が導かれます.
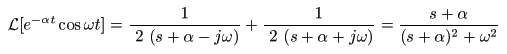
- すなわち,
減衰振動関数
e-αt cos (ωt)
の
ラプラス変換
は,
σ > -α
の収束域で
- F (s) = (s + α) / { (s + α)2+ω2 }
になります.
- ここで,
α = 0
とおくと右辺は
s / ( s2+ω2 )
となり,
例題3
の結果に一致します.
- また,
ω = 0
とおくと
1 / ( s + α )
となり,
例題2
と同じ結果が得られます.
[例題6] 減衰振動関数 f (t) = e-αt sin (ωt) のラプラス変換
- 同様に
α
と
ω
を正の実数として,
減衰振動関数
f (t) = e-αt sin (ωt)
の
ラプラス変換
を求めます.
- cos
の場合と同様に,
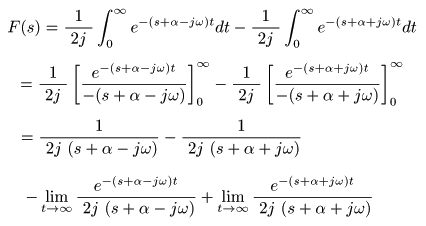
- ここで,複素変数
s
の実部
Re (s)
を
σ
として
σ > -α
のとき,上式の第3項,第4項が
0
となり,
- 以下の式が導かれます.
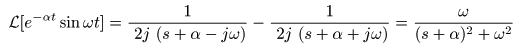
- すなわち,
減衰振動関数
e-αt sin (ωt)
の
ラプラス変換
は,
σ > -α
の収束域で
- F (s) = ω / { (s + α)2+ω2 }
になります.
- ここで,
α = 0
とおくと右辺は
ω / ( s2+ω2 )
となり,
例題4
の結果に一致します.
[補足] 基本になるのは指数関数 ex
- 信号処理
や
微分方程式
の分野で,基本となる最も重要な関数は
指数関数
です.
- 例えば,
フーリエ変換
の
定義
には,
e-jωt
の
指数関数
が組み込まれています.
- 一方,
ラプラス変換
の
定義
には,
収束因子
として
e-st
が含まれており,
- 例題
で示したように,
原関数
f (t)
に
指数関数
を用いたとき,
- その
像関数
F (s)
は
s
を変数とする簡単な
有理式
の形になります.
- 一般に,
指数関数
は,
ex
のように表されますが,厳密には
e
の
x
乗
ではありません.
- なぜなら,
変数
x
が
有理数
のとき,
整数
m
,
n
を用いて,
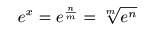
- のように表せますが,
x
が
無理数
の場合や,
e-jωt
のような
複素数
のときは対応できません.
- 実は,
指数関数
の
定義
は以下のようになっており,
x
が
∞
の場合を除き
絶対収束
するので
- 項別
に
微分
することができます.
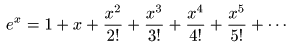
- ここで
自然対数
の
底
e
の
値
2.718…
は,
x
に
1
を代入することにより,次のように定まります.
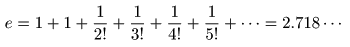
- また,2つの
指数関数
の
積
について
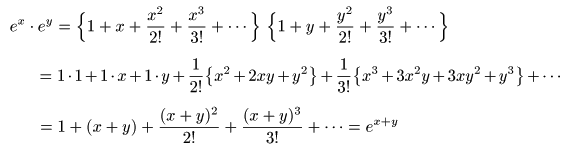
- が成立し,
ex
と
ey
の積の
変数
が
和
x + y
の形で表されます.
- さらに,
ex
を
x
で
微分
すると,
項別微分
可能なので,
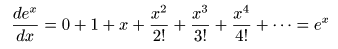
- となり,右辺の項が右側に
1つシフト
しますが,
項数
が
∞
のため実質的に
ex
に等しくなります.
- このように,
指数関数
は
微分
してもその形が変わらない
ただ一つ
の関数
と言えます.
- なお,
変数
x
を
α
倍して
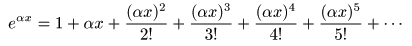
- としたとき,
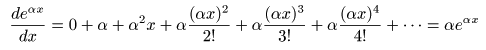
- のようになり,
微分
すると関数の値が
α
倍
される性質があります.
- このような性質を利用して,
微分方程式
の
解
を
代数方程式
により解く方法が用いられています.
[補足] オイラー(Eular)の公式 e jθ = cosθ + j sinθ
- 例題3,4
で示したように,
三角関数
の
cos
や
sin
は,
複素共役
な
2
つの
指数関数
の
- 加減算
で表すことができ,
指数関数
に似た性質を示します.
- それらを結び付けるのが,以下に示す
オイラーの公式
であり,
最も美しい公式
の一つとされています.
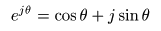
- この式は,
指数関数
の
変数
x
に
jθ
を代入することにより,以下のように導かれます.
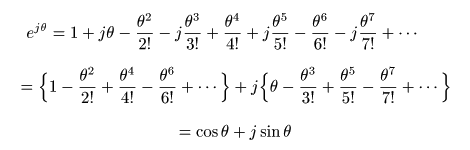
- なお,
cos
や
sin
については,
θ = 0
において
∞回微分可能
であり,
- θ = 0
を
中心
とする
以下の
テイラー展開(マクローリン展開)
の
式
を用いています.
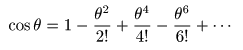
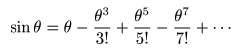
- ここで,
実数
α
,
β
について,
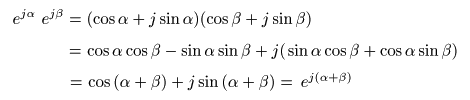
- が成立し,これを
加法定理
と呼びます.
[補足] テイラー展開(マクローリン展開)とは
- ここでは,
オイラーの公式
の証明で用いた
テイラー展開(マクローリン展開)
について補足します.
- x = 0
において
f (x)
が
∞回微分可能
と仮定したとき,
- 以下に示す
x
の
べき級数
を,
f (x)
の
マクローリン展開
と呼びます.
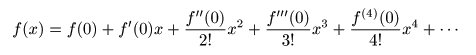
- この
べき級数
が収束し,もとの
f (x)
に一致するとき,
マクローリン展開可能
といいます.
- 以下,この式が導出される過程を示しましょう.
- はじめに,
係数
を
cn (n = 0, 1, 2, …)
として,
f (x)
が以下の
べき級数
で表されるものとします.
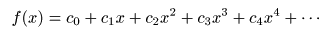
- ここで,
係数
の
c0
については
上式で
x = 0
とおくことにより,
c0 = f (0)
のように求められます.
- 次に,
係数
の
c1
を決定するため
上式を
x
で
微分
します.
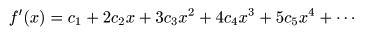
- さらに,上位の
係数
cn
を求めるため,以下のように
微分操作
を繰り返します.
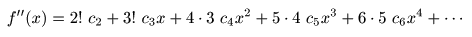
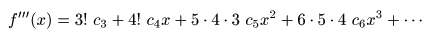
- 微分
したそれぞれの式で
x = 0
とおくことにより,
係数
の
cn
が以下のように定まり,
- これらを上の
f (x)
に代入すると,
マクローリン展開の式
が得られます.
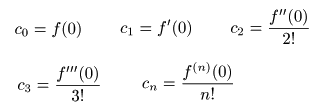
- なお,
f (x)
が
三角関数
の
cos
や
sin
のとき,この級数は
収束
し,
- 以下に示すように,
∞回微分可能
という条件を満たします.
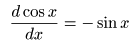
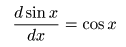
- ここで,
x = 0
とおくと,
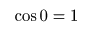
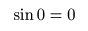
- のようになり,
微分値
が
1, 0, -1, 0
のパターンを繰り返すので,最終的に以下の式が導かれます.
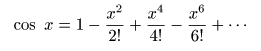
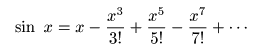
- なお,これらの
無限級数
は
絶対収束
の条件を満たしています.
- ここでは,
x = 0
を中心に展開する
マクローリン展開
について説明しましたが,
- f (x)
が
x = a
において
∞回微分可能
のとき,
x = a
を中心とする次の
べき級数
を
- テイラー展開
と言います.
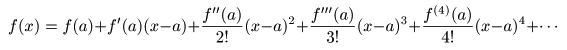
- この級数が
収束
し,元の
f (x)
に一致するとき,
テイラー展開可能
と言います.
[例題7] デルタ関数δ(t)のラプラス変換
- デルタ関数
δ(t)
は,
幅
0
,
面積
1
の
インパルス状
の波形をもつ
仮想的
な関数であり,
- 線形システム
の
応答
等で重要な役割を果たします.
- ここでは,その
ラプラス変換
£[δ(t)]
を求めてみましょう.
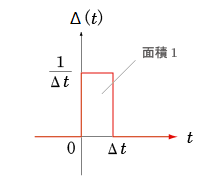
- 始めに,
微少時間
を
Δt
として,下の図に示すような
幅
Δt
,
高さ
1/Δt
の
矩形状
の信号を考えます.
- なおこの矩形の
面積
は,
Δt
の値にかかわりなく
1
になっています.
- 次にこの
ラプラス変換
を計算し,
Δt→0
における極限を,
デルタ関数
の
ラプラス変換
とみなします.
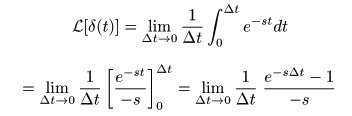
- ここで,先ほど述べた
指数関数
の定義より,
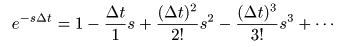
- が成立するので,
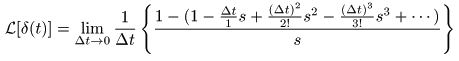
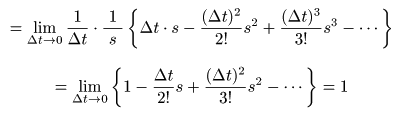
- となり,
£[δ(t)] = 1
が成立することが分かります.
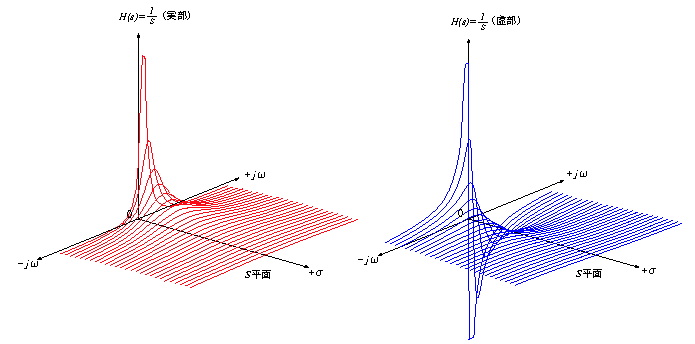
2.2 複素関数 F(s) の表現
- 次に,
複素変数
s
に対応する
複素関数
1 / s
の
表現方法
について整理しましょう.
- 一般的な
実関数
,例えば
f (x) = 1 / x
は,2次元平面上の
双曲線
で表すことができます.
- 一方,
F (s) = 1 / s
のような複素関数では,変数と関数にそれぞれ
実部
と
虚部
があり,
- グラフ表示するためには,
4次元空間
が必要となります.
- このため,ここでは
s
に対する
F (s)
を
実部
と
虚部
に分け,これらを
2つの
3次元グラフ
- で表すことにします.
- なお,複素変数
s = σ + jω
を水平面で表し,これに対する
F (s)
の
実部
と
虚部
を
高さ
で示しています.
- 詳しくは後ほど示しますが,これらは原関数
u (t)
を正の実数
σ
の値に応じて時間方向に減衰させ,
- これを
フーリエ変換
により
スペクトル
に変換したものを
σ
の方向に連続的に拡張したものであり,
- その次元は
スペクトル
の
[f (t)の次元×時間]
になります.
- この図では,
F (s)
の収束域が
σ > 0
となるため,
s平面
の
右半分
のみ表示し,
- 左半分
は発散するため,省略しています.
- ここで,
u (t)
は
実数
であるため,
F (s)
の
実部
は
ω = 0
の実軸について
偶対称
となる
偶関数,
- 虚部
は
奇対称
となる
奇関数
になります.
- すなわち,
- より,
- が成立します.ここで,
-
(
バー
)は,
虚部
の符号
±
を反転させた
複素共役
を表しています.
[補足] ラプラス変換の収束域における物理的イメージ
- 一般に,
ラプラス変換
は
フーリエ変換
に比べ,物理的なイメージが掴み難いと言われますが,
- ここでは,その
イメージ化
を試みます.
- 原関数
f (t)
として
単位ステップ関数
u (t)
を選び,その
像関数
F (s)
の
収束域
における
- イメージを下の図に示します.
- ここでは,
複素変数
s = σ + jω
の実部
σ
を正の一定値とみなして
積分操作
を行います.
- はじめに,指数部を
e-s t = e-σt ・ e-jω t
のように変形し,
原関数
f (t)
と
e-σ t
の積
g (t,σ)
を求めます.
- 次に
e-jω t
を乗じ,
0
から
∞
まで時間
t
で積分します.
- これらの操作を式で表すと,以下のようになります.
- なお,
t < 0
で
u (t) = 0
となるため,
積分範囲
を
0~∞
から
-∞~∞
に変更しています.
- 以上の操作は,一定の
σ
における
g (t,σ)
の
フーリエ変換
に他なりません.
- このように
σ > 0
を固定したとき,
ラプラス変換
F(σ + jω)
は,
原関数
f (t)
と
e-σ t
の積を,
- t = 0~∞
の範囲で
フーリエ変換
した結果に等価です.
- なお,
積分範囲
が
0~∞
のとき,
片側フーリエ変換
と呼ぶことがあります.
- 図の
赤
と
青
の2本の曲線は,
g (t,σ) = u (t) ・e-σ t
という関数の
複素スペクトル
(
実部
と
虚部
)
- を表しています.
- この関数の形状について,
簡単に補足しましょう.
- 正の実数
σ
の値が小さいとき,
g (t,σ) = u (t) ・e-σ t
の形状は時間
t
について,
なだらか
に変化するため,
- 直流付近
に主要な
周波数成分
が集中します.
- その結果,
スペクトル
F (s)
は
s平面
の原点付近で
尖った
形状になります.
- 一方,
σ
の値が大きくなると,
g (t,σ)
は時間
t
について
インパルス
のように
尖った
形状となり,
- その
スペクトル
F (s)
は低レベルながら,低域から高域にかけて広く分散し
平坦
になります.
- なお,
複素変数
s
の実部
σ
は離散値ではなく,
連続的
に変化することに注意が必要です.
- このように,
ラプラス変換
F(σ + jω)
は
s
の実部
σ
を一定に保ちながら,
- 原関数
f (t)
に
u (t) ・e-σ t
を乗じた関数を
(片側)フーリエ変換
して求めた
スペクトル
を,
- s平面
の右側にある
収束域
に2次元状に拡張したものです.
[補足] 逆ラプラス変換の物理的イメージ
- 次に,逆の操作である
逆ラプラス変換
の
イメージ
を探ってみましょう.
- 逆ラプラス変換
の
定義
では,積分路が
σ - j ∞
から
σ + j ∞
となっています.
- すなわち,虚軸に平行で実部が
σ
となる直線上を,
ω
について
-∞
から
+∞
まで積分します.
- 逆ラプラス変換
では
s
の増分
ds
を用いて積分するため,
- σ
が一定となる
積分路
の場合,その
増分
は
ds = j dω
で表されます.
- このため,
定義式
の係数
1/(2πj)
の
j
の項が消え,
逆フーリエ変換
の式が導かれます.
- 単位ステップ関数
u (t)
の
ラプラス変換
は
F (s) = 1 / s
となりますが,
- これを
逆ラプラス変換
すると,元の
単位ステップ関数
u (t)
が再現されることを示しましょう.
- 下の図の
赤
と
青
の曲線は,
σ > 0
となる直線状の積分路における
u (t) ・e-σ t
という関数の
- 複素スペクトル
を表しています.
- 同じ値の
σ
を用いてこの
複素スペクトル
を
逆フーリエ変換
すると,
u (t) ・e-σ t
が
- 再現されることは明らかです.
- この結果を
e-σ t
で割ると,(すなわち
eσ t
を乗じると),原関数の
ユニット関数
u (t)
が得られます.
- これらの
操作
を式で表すと次のようになります.
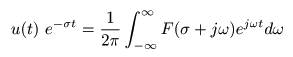
[参考] 逆ラプラス変換の積分路の不自然さ
- ところで,上の図を眺めていると,ある
不思議
なことに気付きます.
- それは,
原関数
f (t)
を復元するためには
F (s)
の値を
s
の
全領域
にわたって求める必要はなく,
- σ > 0
となる
任意の積分路
における
F (s)
の値があれば十分であるという事実です.
- すなわち,
積分路
の選び方にはある
自由度
が残されています.
- さらに,
逆ラプラス変換
の定義式では,
変数
s
の扱いが
積分記号
の内側と
積分路
で異なっており,
- 一種の
不自然さ
が感じられます.
- 例えば
収束因子
e-st
の複素数
s
は,
s平面
上の1点を,
ds
は
s平面
上の微小な
変化量
を表しており,
- これらは
直交座標
や
極座標
などの
座標系
に依存しない
一般的な表現
が用いられています.
- 一方,
積分路
については,
水平軸の
σ
に直交する
直線上
を実数の
ω
で積分しています.
- すなわち,
直交座標系
が指定されており,
これを
ブロムウィッチ積分
と呼びます.
- 式の表現上の
統一性
から類推すると,
直交座標
や
極座標
などに依存しない複素表現の
積分路
による
- 定義式
があっても不思議ではありません.
- 詳しくは次節で述べますが,
一般化した複素表現の積分路
C
を用いて,
原関数
f (t)
と
像関数
F (s)
を結び付ける
- 新たな
関係式
が存在し,これを
複素関数
の
著名な定理
から導出することが可能です.
- その本質を理解するためには,
正則
な
複素関数
や
複素積分
の性質に関する知識が必要となりますが,
- 詳細は
専門書
等に委ねることにして,
次節でその
概要
を紹介します.
3. 解析接続による像関数 F(s) の拡張
- フーリエ変換
では,
像関数
の
F (ω)
が
複素スペクトル
という
物理量
を表しており,
- 入力信号やシステムの特性を評価する
有用な指標
として,
F (ω)
の形状が議論されます.
- 一方の
ラプラス変換
では,
像関数
の
F (s)
は
拡張
された一種の
スペクトル
を表していますが,
- それ自体が
物理的な指標
として用いられることはほとんどなく,
ある
原関数
f (t)
に
- ひとつの
像関数
F (s)
を対応付ける
数学的写像
の一手法として扱われます.
- 本節では,その抽象度を高めることにより
ラプラス変換
を
スペクトル
の束縛から解放し,
- 解析接続
という手法を用いて,従来の
像関数
を
s平面
全体に拡張した新たな
像関数
の性質について検討します.
3.1 ラプラス変換の収束域について
- フーリエ変換
では積分値が
発散
し,その
スペクトル
が確定しないケースがしばしば発生します.
- 例えば,
f (t) = 1
の
フーリエ変換
F(ω)
では,
ω = 0
のとき
1
という値を
- ∞
から
+ ∞
まで積分するため
- ∞
に
発散
します.
- このため,実際には存在しない
超関数
の
デルタ関数
δ(ω)
を導入する必要がありました.
- 一方の
ラプラス変換
では,
Re (s) = σ
の値を大きく設定することにより,積分の
収束性
が高まりますが,
- 像関数
の
F (s)
ごとにその
収束域
を考慮する必要があります.
- 例えば,
単位ステップ関数
の
像関数
F (s) = 1 / s
に
s = -1
を代入すると,
-1
という値が得られます.
- この
-1
という値は,もはや
スペクトル
を表していません.
- なぜなら,
このとき
Re (s) < 0
となり,
ラプラス変換
を計算する過程で
0
に収束するということで消え去った
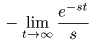
- という項が
∞
に発散するためです.
- このため,
スペクトル
も
∞
に発散します.
- ラプラス変換
が
スペクトル
という
物理量
を表現する限り,
このような
収束性
を
- 無視することはできません.
- そこで,その抽象度を高めることにより,
スペクトル
という
物理量
による拘束から解放し,
- 極めて有用な
解析手段
となる
ラプラス変換
の
新たな解釈
を示します.
3.2 像関数 F(s) の定義域拡大
- ここでは
ラプラス変換(狭義)
の
収束域
において,その
像関数
F (s)
に完全に一致し,
- s
平面全体で
定義
される新たな
複素関数
F~(s)
について検討します.
- このような操作を
解析接続
と呼びますが,その詳細は後ほど述べることにして,
- 具体的な例を用いて説明しましょう.
- 先に示したように,
原関数
f (t)
が
単位ステップ関数
のとき,その
像関数
は
F (s) = 1 / s
となり,
- その
収束域
は
s
平面
の右半分になります.
- 下の図は新たな
像関数
の
F~(s) = 1 / s
を表していますが,その
定義域
が
s
平面
全体に
- 拡張されており,
s = 0
を除く,すべての
s
について
F~(s)
の値が存在します.
- すなわち,
F~(-1) = -1
が成立します.
- いうまでもなく,
Re (s) = σ > 0
の
収束域
では
f (t) = u (t)
の
像関数
F (s)
に一致しています.
- 図の左は
F~(s)
の
実部
,
右は
虚部
を表しており,
いずれも
s = 0
で
∞
に発散します.
- ここで,
変数
s
の
±の符号
を反転させると
F~(-s) = - 1/s = - F~(s)
となり,
- s = 0
の
原点
について
奇対称
の関係になっています.
- すなわち,
収束域
である
s平面
の右側の値が,
原点
について点対称となるよう
- 左反面
に射影されています.
- また
実部
を,
垂直な回転軸
を中心に
90°
回転させると
虚部
に一致します.
- このように
解析接続
された新たな
像関数
F~(s) = 1 / s
は,
s = 0
の
原点
を中心とする
- 対称性
があり,
原点
を除いて
有限
な値となります.
- なお
ラプラス変換
の
定義
に立ち戻ると,
0~∞
の
定積分
において
t = 0
の項のみに着目し,
- t = ∞
の
項
は無視しています.
- 一般には
F~(s)
と
F (s)
はその
収束域
が異なるだけで,実質的な違いはありません.
- 本資料でもこれに倣い,これ以降
F~(s)
を単に
F (s)
と記述することにします.
3.3 像関数 F (s)の特徴量とは?
- 一般に,
像関数
F (s)
の
全体
と
部分
は,ある
統一
された
シンプルな法則
により支配されており,
- 一定の
特徴量
により記述されます.
- 例えば
例題2
で示したように,
指数関数
e-αt
の
像関数
F (s) = 1 / (s + α)
の
形状
を決定する
- パラメータ
は
2つ
あり,
分母
が
0
となる
s
の値
-α
と,
分子
の
1
になります.
- この
-α
は,上の図の
縦軸
の値が
∞
に発散する
s平面
上の位置を示しています.
- なお,
s = -α
において
F (s)
は
∞
に
発散
しますが,それ以外は
有限な値をもちます.
- すなわち,
F (s)
にはその
大きさ
や
向き
を表す指標が存在し,
分子
の
1
という値がそれに相当します.
- 山に例えると,
1つ目の
パラメータ
は,縦軸
が
±∞
に発散する
ピーク
の
水平面内
の
位置
であり,
- 2つ目の
パラメータ
は,
有限
な部分の
高さ
やその
向き
を決定する
係数
に相当します.
- なお,この例の
パラメータ
は
実数
でしたが,一般には
複素数
となることに注意が必要です.
- このとき
ピークの位置
とその
高さ
を決めれば,
山麓
の部分的な地形が完全に定まります.
- 逆に,
山麓
の部分的な地形が決まれば,
ピークの位置
や
高さ
,さらに
頂上の反対側
の地形等が
- すべて定まります.
- このような性質により,任意の
σ > 0
に対応する
積分路
を用いて,
像関数
F (s)
を
ω
で積分した場合でも,
- 原関数
f (t)
が復元されるわけです.
- 次に,
単位ステップ関数
u (t)
以外の
像関数
F (s)
の
形状
について調べてみましょう.
- 下の図では,
原関数
f (t)
が
単位ステップ関数
⇒
指数関数
⇒
減衰振動関数(cos)
⇒
三角関数(cos)
⇒
- 単位ステップ関数
⇒
…
のように連続的に推移しています.
- これらは,それぞれ
例題1
,
例題2
,
例題5
,
例題3
に対応しています.
- 振動しない
単位ステップ関数
と
指数関数
では,
ピーク
の数はともに
1つ
で同じ形状をもち,並行シフトすると重なります.
- 一方,
振動を伴う
減衰振動関数(cos)
と
三角関数(cos)
の場合,回転方向が異なる2つの
コイルばね
の
- 重ね合わせ
で表されるので,
2つ
の
ピーク
が現れます.
- なお,これらは虚部の±の符号を反転した
複素共役
の関係にあります.
[補足] 正則な複素関数とは?
- 複素関数論
では,しばしば
正則関数
や
孤立特異点
,
極
,
留数
などの概念が用いられます.
- 厳密な
定義
や関連する
定理等
を記述すると,
ラプラス変換
の範疇を逸脱するので,
- それらは関連する
専門書
等に委ねることにして,
ここではその
イメージ
を中心に説明します.
- 初めに
正則
という概念について示します.
- 複素平面
のある
開集合
D ∋ s
のあらゆる点
s
において,
複素関数
g (s)
が
微分可能
であるとき,
- この関数は
D
において
正則
となります.
- s = s0
において
微分可能
とは,
s0
への近づき方によらず,以下に示す値が
一定
の場合を指します.
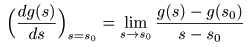
- ここで注意しなければならないのは,
1つの点
s0
において微分可能であっても
正則
とはいえないことです.
- このとき,
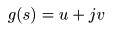
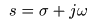
- として,以下に示す
コーシー・リーマンの方程式
が導かれます.
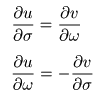
- 上で示した
微分
の
定義
から,実軸の
σ
と,虚軸の
jω
に沿って
偏微分
した結果が等しくなり,
- 以下の式が成立します.
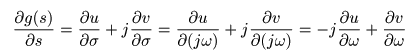
- この式の
実部
と
虚部
を比較することにより,
コーシー・リーマンの方程式
が導かれます.
- 複素平面
では,ある点
s0
への近づき方が
上下左右
の
2次元的
な広がりをもつので,
- 実関数
の
微分可能
に比べより強い制約が課され,
結果として
実関数
からは想像できない
- シンプル
で
美しい性質
が付与されます.
- 一方,
正則な領域
D
の内部にあって,
s
平面
を
反時計方向
に
一周
する任意の
単一閉曲線
C
について
- 周回積分
した値は
0
になります.すなわち,
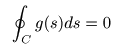
- が成立し,これを
コーシーの積分定理
と呼びます.
- この定理は,
グリーンの定理
と
コーシー・リーマンの方程式
から導くことができますが,
- この後で述べるように,
正則
な
領域内
で
積分路
を変更しても
積分
の結果は
- 影響を受けない根拠となっています.
[補足] 複素関数の特徴が投影される孤立特異点
- 複素関数
g (s)
の
分母
が
0
となる
s
のことを
特異点
と呼びます.
- この
特異点
は,
極
,
真正特異点
,
分岐点
に分類されますが,ここで扱うのは
極
です.
- 以下,具体的な例で説明しましょう.
- 例えば,
n
が
正の整数
のとき,次の
g (s)
は
無限遠点
s = ∞
を除いて
正則
となります.
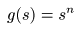
- さらに項数が増えた
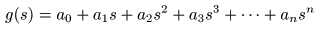
- についても,同様に
無限遠点
s = ∞
を除き
正則
となります.
- 一方,
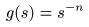
- の場合は,
原点
s = 0
を除いて
正則
となり,この
孤立特異点
を
n 位の極
といいます.
- また,
正の整数
m
について
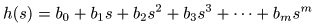
- として,
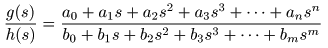
- の場合,
分母
の
h (s)
が
0
となる
m
個の
孤立特異点
を除いて
正則
となります.
- なお,この場合の
個数
は,
重解
を複数にカウントした値です.
- これらの
特異点
では,
複素関数
の値が
∞
に発散するので,例外的な事象と
- 感じられるかもしれませんが,
むしろ
複素関数
の性質を特徴付ける
顔
のような存在と
- 考えることができます.
[補足] 複素関数の周回積分について
- 一般に,
複素関数
についても
実関数
と同様,
微分
や
積分
を定義することができます.
- 例えば
n
を整数として,
1価関数
の
f (s) = sn
を
s
で
微分
すると,
f ' (s) = n sn-1
が得られます.
- 同様に,
f (s) = sn
を
積分
すると,
∫f (s) ds = sn+1 / (n + 1) + 定数
の形になります.
- ここで扱うのは,
s平面
上のある
曲線
に沿った
線積分
であり,
いわゆる
定積分
に相当します.
- さらに,
積分路
の
始点
と
終点
が一致するとき,
周回積分
となります.
- 実関数
の場合,
始点
と
終点
が一致すれば,その
積分値
は
0
になりますが,
- 複素関数
では少し
異なる性質
が現れます.
- ここでは,
複素関数
f (s) = sn
を
原点
を中心に,
反時計方向
に
周回積分
する場合について,
- 下の図を用いて説明しましょう.
- 積分操作
では,
変数
s
の
変分
Δs
は,
σ
の正の軸上から
反時計方向
に
1周
します.
- 例えば,
f (s) = 1
のとき,
変分
Δs
を
積分路
C
に沿って加算したものであり,
-
その
累積値は,
図の中央に示すように
C
に一致します.
- このとき,
定積分
の
始点
と
終点
が
一致するため,その
積分値
は
0
になります.
- 一方,
f (s) = s
を
周回積分
すると,その
積分値
は原点を中心に
2周
することになり,同様に
- 始点
と
終点
が一致するので
0
となります.
- 同様に,
f (s) = s2
の
周回積分
も
0
となります.
- これらの
複素関数
は,いずれも
無限遠点
を除く
s平面
全体で
正則
となり,
- 先に示した
コーシーの積分定理
の結果に一致します.
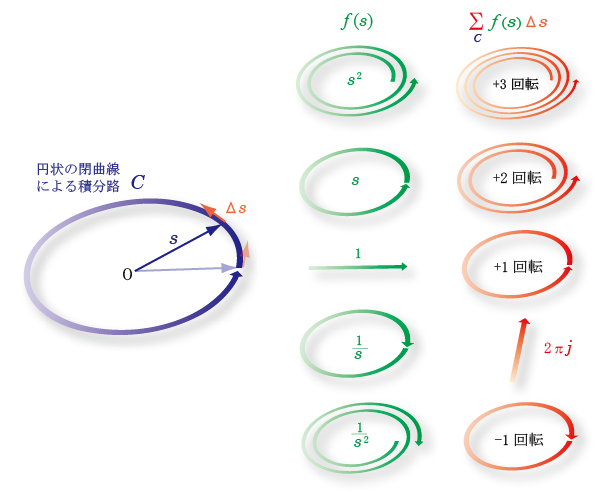
- 次に,
f (s) = sn
が
正則
とはならない
n < 0
の場合について整理しましょう.
- 例えば,
n = -1
すなわち,
f (s) = 1 / s
のとき,
s = 0
は
孤立特異点
となり,
- 1 / s
の値は
σ
の正の軸上から
時計方向
に
1周
します.
- このとき,図のように
変分
Δs
の回転成分が打ち消され,
jω
方向の
純虚数
になります.
- これより,
積分路
C
に沿って1周すると,その積分値は
2πj
となることが分かります.
- 一方,
f (s) = 1 / s2
のとき,その値は,図のように
時計方向
に2回転します.
- このため,その
積分値
は,時計方向に1回転することになり,
- 始点
と
終点
が
一致するので,その
積分値
は
0
になります.
- このように,
複素関数
の
f (s) = sn
を,その
孤立特異点
を1周するよう
周回積分
- するとき,その
積分値
は,
n = -1
のとき
純虚数
2πj
となり,
- それ以外は
0
となることが分かります.
[補足] 留数とは?
- 次に,
留数
について説明します.
- 複素関数
f (s)
が
s = a
に
孤立特異点
をもつとき,
s = a
における
留数
は以下のように定義されます.
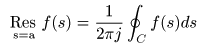
- ここで,
積分路
の
C
は,
s = a
を中心に反時計方向に1周する
単一閉曲線
です.
- 例えば,
孤立特異点
が
1位
の
極
であるとき,
その
留数
は次のように求められます.
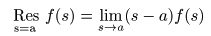
- 先ほどの図で示したように,
像関数
の形状を決定する
パラメータ
は,山の
ピークの位置
とその
高さ(+ 向き)
です.
- 複素関数
の用語を用いると,
ピークの水平面内の位置は
孤立特異点(極)
,山の高さ(+ 向き)は
留数
になります.
- なお,
原関数
が
指数関数
のとき,像関数の分母が
s
の
1次式
となるので,
1位の極
となります.
- 例えば,
原関数
f (t)
が
単位ステップ関数
u (t)
の場合,
像関数
は
F (s) = 1 / s
となるので,
s = 0
が
1位の極
,
- その
留数
は
1
となります.
- 同様にして,例題2の
指数関数
の場合,
像関数
は
F (s) = 1 / (s + α)
となるので,
s = -α
が
1位
の
極
,
- その
留数
は
1
となります.
- 三角関数
の
cos (ωt)
の場合,
1位
の
極
が
2つ
現れ,
s = jω
と
s = -jω
になります.
- また,
留数
はいずれも
1/2
です.
- 一方,
sin (ωt)
の
極
は
cos (ωt)
の場合と同じですが,それらの
留数
は
1/2 j
と
-1/2 j
という
- 共役複素数
になるので,注意が必要です.
- n
を
正の整数
として
原関数
が
t n
で表されるとき,
その
像関数
F (s)
の
分母
は
s
の
(n + 1)
次式
となります.
- この場合の
孤立特異点
を
(n + 1)
位
の
極
と呼びますが,その詳細については後ほど説明します.
- なお,ここでは
像関数
F (s)
単体の
留数
を示しましたが,
ラプラス逆変換
の場合
F (s) est
の
留数
を
- 扱うことあるので混同しないよう注意が必要です.
[参考] 等角写像について
- 先に述べたように,
s
平面
のある
領域
D
で
正則
な
複素関数
は,
D
内のあらゆる点
a
において,
- コーシー・リーマンの方程式
が成立します.
- このとき,
s
平面
の
a
点とその近傍の
2点
がなす
角度
は,
F (s)
平面
の
F (a)
と
- その近傍の
2点
がなす
角度
に等しくなる性質があります.
- これを
等角写像
と言います.
- 次の図に,この
等角写像
の
イメージ
を示します.
- なお,これまでの表示法と異なり,左が
s
平面,右が対応する
像関数
F (s) = 1 / s
の平面を表しています.
- この場合,左側の
赤
と
青
の点は,それぞれ右の
赤
と
青
の点に対応しています.
- この図で,
赤
と
青
の直線群あるいは曲線群が,互いに
直角に交差
していることに注意して下さい.
3.4 解析接続とは?
- ラプラス変換(狭義)
の
収束域
において,その
像関数
F (s)
に完全に一致し,
- 極
などの
孤立特異点
を除いて
s
平面全体で
正則
となる新たな
複素関数
F~(s)
が
- ただ1つ存在します.
- これは,複素関数における
一致の定理
から導かれます.
- この
像関数
F (s)
を
解析接続
することにより,
F~ (s)
が得られます.
- 以下,原関数として
単位ステップ関数
u (t)
を選び,その
像関数
F (s) = 1 / s
について,
- 具体的な
解析接続
のイメージを示します.
- 像関数
F (s) = 1 / s
の収束域は,
Re (s) > 0
,すなわち
s平面
の
右半分
になります.
- この
収束域内
に点
s = a
を選んで,この点を中心とする
小さな円
を設定し,
- 特異点
を跨がないようにして
その半径を増やしてゆきます.
- 下の図に示すように,点
a
の選び方によっては,この
円の領域
は
s平面
右側の
- 収束域
をはみ出すことがあります.
- 次に,はみ出した
円の領域内
に新たな点
b
を設定し,上と同様の処理を繰り返すことにより,
- この
領域
を次々に拡大してゆきます.
- この領域は,最終的に
特異点
s = 0
を除く
s平面
全体に拡がります.
- 以上の操作がいわゆる
解析接続
であり,最終的に
F (s)
から
F~(s)
を導くことが可能です.
- この
解析接続
では,先に述べた
テイラー展開
を用います.
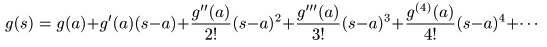
- ここで
像関数
f (s) = 1 / s
の
導関数
は,以下のようになります.
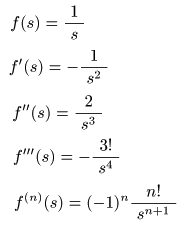
- これより
a ≠ 0
のとき,
f (s)
は
s = a
において,以下のような
べき級数
で表されることが分かります.
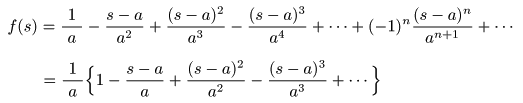
- この
べき級数
は
等比級数
となり,その
公比
は
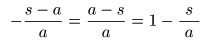
- となることから,
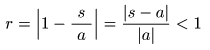
- の条件を満たすとき収束します.
このとき,
f (s)
は,
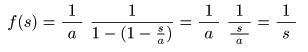
- のようになり,この円内の任意の
s
について,円の中心
a
と同じ
f (s) = 1 / s
という関係が成立します.
- なお,収束の条件は
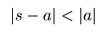
- のように表すことができます.
- これは,中心が
s = a
,半径が
|a|
の円の内部を表し,その境界はすべて
特異点
s = 0
を通ります.
- すなわち,
収束域
内の点
s = a
を中心とする
円の内部
のすべての点は,
- 1 / s
という関数で表されることが分かります.
- このような操作を繰り返すことにより,
収束域
の外部へ
1 / s
という関数で表される領域を
- 次々に拡張することが可能です.
3.5 原関数と像関数の対応
- 基本的な
原関数
とその
ラプラス変換
の
対応関係
を,以下の表に示します.
- なお,これらの
像関数
はいずれも
1位の極
をもっています.
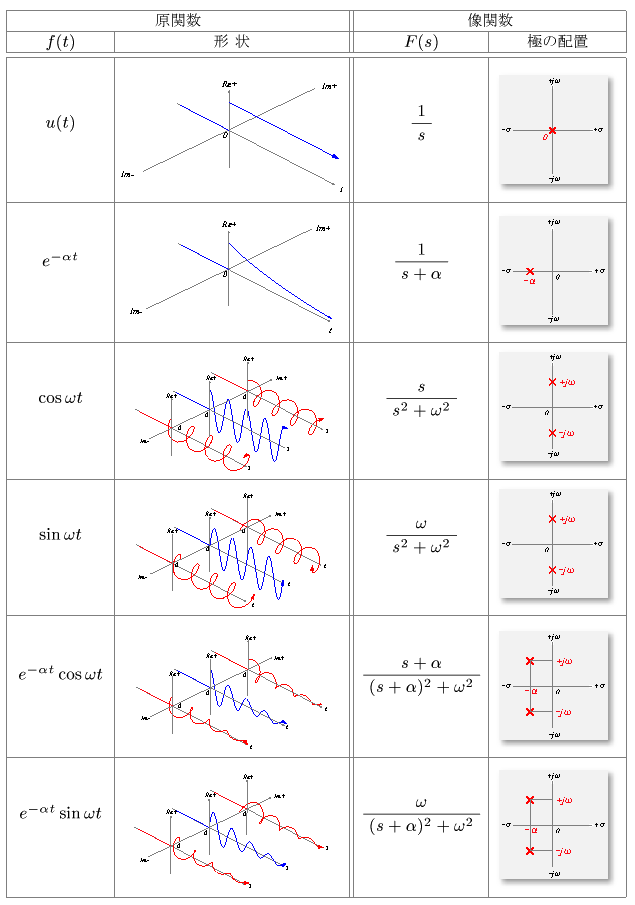
- このように,
原関数
f (t)
が
指数関数
や
三角関数
の場合,
対応する
極
と,その
留数
から,
- 簡単にその
像関数
F (s)
を求めることができます.
[補足] 逆ラプラス変換とコーシーの積分公式について
- ここでは,像関数
F(s)
が
1位の極
をもつとき,
逆ラプラス変換
は
コーシーの積分公式
において,
- g (s)
を
指数関数
とした場合に一致することを示します.
- はじめに
コーシーの積分公式
を示します.
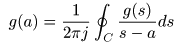
- この式で,
g (s)
は
領域
D
において
正則
となる任意の関数であり,
- a
は
領域
D
における任意の点,
積分路
の
C
は
領域
D
内にあり,
- 点
a
を正方向,すなわち
反時計方向
に1周する
単一閉曲線
とします.
- この
公式
は,以下の
テイラー展開
の式から導かれます.
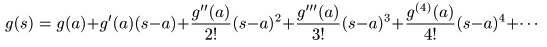
- この式を
積分公式
の右辺に代入します.
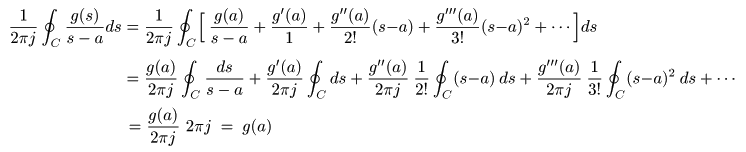
- ここで,先に述べたように
1 / (s - a)
の
周回積分
は
2πj
となりますが,他の項はすべて
0
となることを用いています.
- 次に,
g (s)
を次の
指数関数
とします.
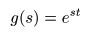
- このとき
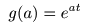
- となり,
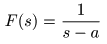
- とおくと,
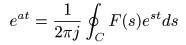
- が導かれます.
- この式において
a
を
-a
に置き換えます.すなわち,
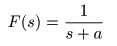
- のとき,
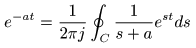
- が成立し,
積分路
C
を除くと
逆ラプラス変換
の式に一致します.
- これより,
原関数
の
e-at
と,
像関数
の
1 / (s + a)
が,1対1に対応することが分かります.
[参考] 像関数 F (s) の積分路について
- コーシーの積分定理
と
積分公式
から,
孤立特異点
を
反時計方向
に1周するという条件を満たしさえすれば,
- 積分路
C
は
自由
に変更することができます.
- その
積分路
を変更するイメージを下の図に示します.
- はじめに,
ジョルダンの補助定理
を用いて,
直線状の積分路
に半円状の経路を追加し,
- 反時計方向
に
周回する積分路
に変更します.
- 次に,
コーシーの積分定理
を用いて,
孤立特異点
を跨がないよう,
周回積分
の経路を修正します.
- 経路長
を短くしてゆくと,最終的に
孤立特異点
を周回する2つの円状の積分路に到達します.
- すなわち,
周回積分
の値は,最終的に
孤立特異点
の位置とその
留数
のみにより定まることを示しており,
- これから,いわゆる
留数の定理
が導かれます.
[参考] 次元の自然な拡張について
- ここでは,
フーリエ級数
,
フーリエ変換
,
ラプラス変換
における処理の
次元
が,
- 2次元
(
振動
)
→
3次元
(
回転
)
→
4次元
(
発散・収束を伴う回転
)
のように,
- 自然な
拡張関係
にあることを示します.
- それらを図示すると,
次の図
のようになります.
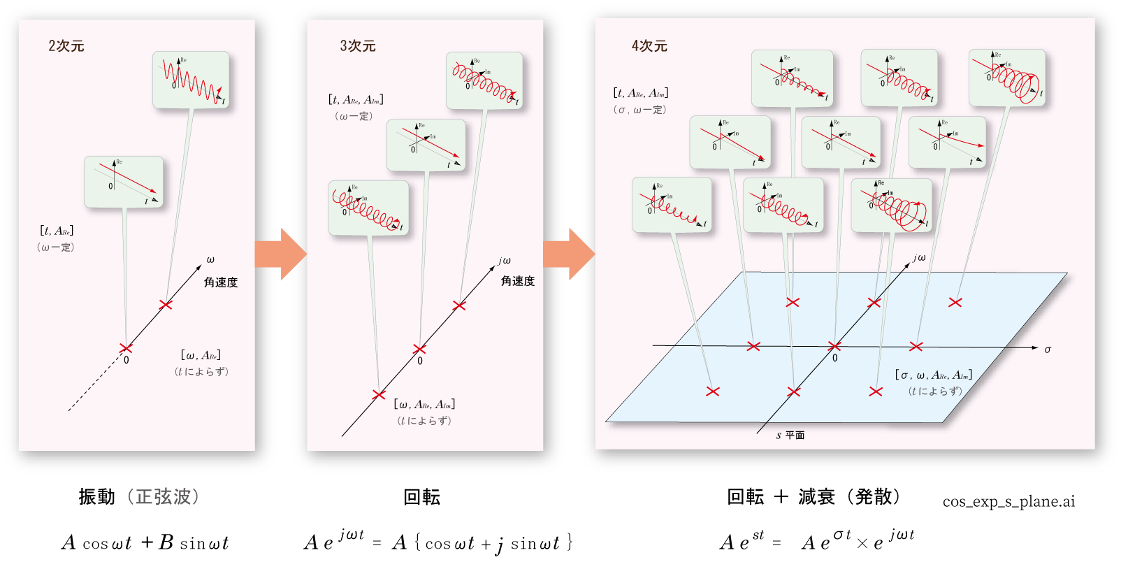
- 第3章で示した
フーリエ級数
は,任意の
周期関数
を,その
整数分の1
の
周期
をもつ
- sin
や
cos
の
振動成分
の
重ね合わせ
により表現するものです.
- 図の左に示すように,この
2次元波形
の
横軸
は
時間
t
,
縦軸
は
実関数
f(t)
の値を表しています.
- 一方,
2次元信号
f(t)
を構成する
sin
や
cos
の
振動成分
について,
- これらと
直交
する
新たな軸(虚軸)
を追加することにより,
- 3次元
の
回転モデル
に
拡張
することが可能です.
- 図の中央は,
角速度
ω
で
回転
する成分(
コイルバネ
)を表しています.
- sin
や
cos
の
振動成分
は,互いに
逆方向
に
回転
する2つの成分(
コイルバネ
)の
- ベクトル加算
により表すことができ,これらは互いに
共役
な2つの
複素数
に対応しています.
- フーリエ変換
(
複素フーリエ級数
)は,信号の
f(t)
から
コイルバネ
の
半径
とその
位相
を
- 求めるプロセスに他なりません.
- この
フーリエ変換
では,
純虚数
の
jω
を用いて,
回転現象
を
ejωt
のように表現していますが,
- この変数に
実部
を加え一般的な
複素数
s=σ+jω
に拡張すると,自動的に
ラプラス変換
が導かれます.
- なお,
次元
は1つ増え
4次元
となっています.
- このとき,
コイルバネ
の
半径が一定
という制約がとれ,
- 図の右に示すように,
指数関数
で
発散
したり
減衰
する性質が付加されます.
- 次に,その
次元
を
拡張
することにより,
現象
がより
簡潔
に表現できる例について具体的に説明しましょう.
- はじめに,
2次元の振動
と
3次元の回転
の関係について整理します.
- 2次元の振動
,すなわち
正弦波
に関する
加法定理
を以下に示します.

- これらの
式の正しさ
を
直感的
に捕らえることは容易ではありませんが,
- 回転
の
加法定理
は極めて単純です.
- すなわち,
角度
α
だけ回転した後,さらに
角度
β
回転
させると,
- 最終的な
角度
はそれらの
和
(α + β)
になっているというものです.
- なお,この式に先に述べた
オイラーの公式
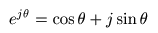
- を代入して
分配則
を適用し,
左辺
と
右辺
の
実部・虚部
を比較することにより,
- 上で示した
正弦波
の
加法定理
が導かれます.
- すなわち,数学的には
回転
の方が
振動
より
簡潔
に表現されることは明らかであり,
- 実数
の
ω
は,自然に
複素数
の
純虚数
jω
に拡張されることになります.
- なお,これ以外にも
基礎数学
や
量子力学
等の分野において,その
次元
を増やすことにより,
- 様々な現象をより
簡潔
に説明できることが知られています.
- 例えば,
トポロジー
の
超難問
である
ポアンカレ予想
を,わかり易く解説するテレビ番組がありましたが,
- その中で,
ジェットコースター
の
走行路
を用いた説明が用いられていました.
- その
走行路
は,
3次元空間
における1つの
閉曲線
であり,
- 当然のことながら,
衝突
を避けるためそれらは1点で
交差
することはありません.
- 一方,その
走行路
が地面に落とす
影
は,
2次元平面
における
閉曲線
になります.
- この
閉曲線
には,
交差
する点がいくつか現れることがあり,
- その場合数学的な扱いは
3次元
の場合よりむしろ
複雑
になります.
- 先に述べた
正弦波
の
加法定理
が複雑になる理由も,その
影
を扱うことに起因します.
- このように,
次元が低い
方が必ずしも
簡潔
に表現できるというわけではなく,
- 対象を記述するのにふさわしい
適切な次元
を見出すことが重要になります.
- 次に,
(片側)フーリエ変換
と
ラプラス変換
の関係について,整理してみましょう.
- 本章では,
ラプラス変換
について解説してきました.
- そこでは,
定義式
に沿って積分値を計算し,
- 解析接続
によりその
収束域
を
特異点
を除く
s
平面全体
に
拡張
するという
- 2段階の構成法
を採用していました.
- しかしながら,ある
関数
f(t)
の
片側フーリエ変換
F(jω)
が収束する場合,
- 虚軸上
の
jω
を
複素平面
の
s=σ+jω
に
解析接続
することにより,
- 直接
ラプラス変換
に
拡張することが可能です.
- その
具体例
を以下に示しましょう.
- α
が
正の実数
のとき,
関数
e-α t
を
片側フーリエ変換
すると,
- その
像関数
F(jω)
は以下のようになります.
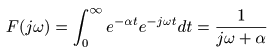
- ここで,
純虚数
の
jω
を
s
平面
に直接
解析接続
することができ,
- その結果として以下の式が導かれます.
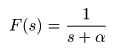
- これは,
関数
e-α t
の
ラプラス変換
に他なりません.
- これより,
ラプラス変換
は
(片側)フーリエ変換
の自然な
拡張
になっていることが理解できると思います.
[参考] ローラン展開について
- マクローリン展開(テイラー展開)
では,例えば
原点
s = 0
における
n次導関数
f (n) (0)
を用いて,
- 原点
近傍の
s
における
f (s)
の値を,
s
の
べき級数
で表現します.
- このため,例えば
原点
s = 0
が
孤立特異点
であるとき
f (s) = ∞
となり,
- 微分値
自体が
存在しない
ので
展開
できません.
- ここでは,
孤立特異点
であっても,それを中心とする
べき級数
に
展開可能
な
- ローラン展開
について説明します.
- はじめに,
下の図のように
原点
O
と
s1
の
孤立特異点
に挟まれた
正則
な
円環領域
を定義します.
-
次に,この領域内にある点
s
を
周回積分
する
積分路
C
を決定します.
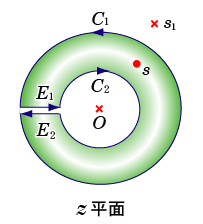
- ここで,
積分路
の
C
は,
C1
,
E1
,
C2
,
E2
に分解することが可能です.
- なお,
積分路
の
E1
と
E2
は方向が逆向きのため,互いに打ち消しあって
0
になります.
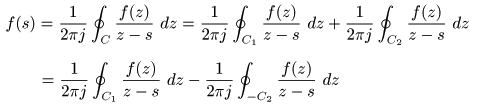
- はじめに,
積分路
C1
上の点
z
について,
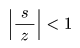
- の条件が成立するので,
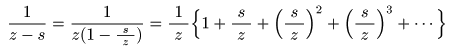
- の
無限級数
で表すことが可能です.このとき,
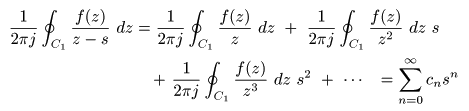
- のような
s
の
多項式
で表されます.ここで,
n ≧ 0
として
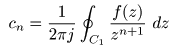
- となります.
- 同様に,
積分路
C2
上の点
z
について
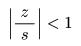
- となるので,
無限級数
の
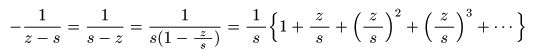
- が成立し,
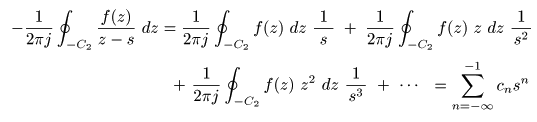
- となるので,
負の整数
n
を用いて
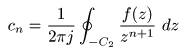
- が成立します.
- ここで,変数
の
z
は,
正則
な
円環領域
にあるので,
係数
cn
の
積分路
C1
,
C2
を変更することができ,
- 最終的に1つの
積分路
C
に統一することが可能です.
- これらをまとめると,一般的な
整数
n
を用いた
多項式
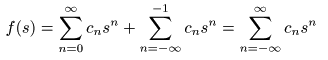
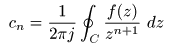
- が導かれます.
- マクローリン展開
では,係数の
Cn
が
f (s)
の
微分形式
で表されていたのに対し,
- この
ローラン展開
では,
f (s)
の
積分形式
で表現されていることに注意が必要です.
- これまで,
像関数
F (s)
が
1位の極
となる場合について検討してきました.
- 次に,
極
が
2位以上
になる事例について検討してみましょう.
[例題8] f (t) = t のラプラス変換
- 原関数
f (t)
が
t
の1次式,例えば
f (t) = t
のとき,その
像関数
F (s)
は
部分積分の公式
を用いて,
-
次のように求められます.
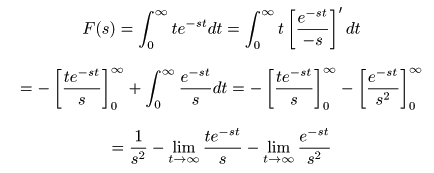
- ここで,
Re(s) = σ > 0
のとき,上式の第2項と第3項が
0
となり,
以下の式が導かれます.
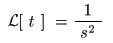
- すなわち,
f (t) = t
の
ラプラス変換
は,
σ > 0
の収束域で
F (s) = 1 / s2
となり,
- s = 0
に
2位の極
をもちます.
[例題9] f (t) = t2のラプラス変換
- 原関数
f (t)
が
t
の2次式,例えば
f (t) = t2
のとき,その
像関数
F (s)
は
部分積分
を
- 2回繰り返すことにより,次のように求められます.

- ここで,
Re(s) = σ > 0
のとき,上式の第2項以降がすべて
0
となり,最終的に
以下の式が求まります.
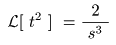
- すなわち,
f (t) = t2
の
ラプラス変換
は,
σ > 0
の収束域で
F (s) = 2 / s3
になり,
- s = 0
に
3位の極
をもちます.
[例題10] f (t) = tnのラプラス変換
- 例題8
,
例題9
より,
n
を
正の整数
として
f (t) = tn
の
像関数
は,次のようになることが分かります.
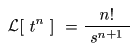
- なお,
その
像関数
F (s)
の収束域は
σ > 0
で,
s = 0
に
(n + 1)位の極
をもちます.
[例題11] f (t) = t e-αtのラプラス変換
- 同様にして,
f (t) = t e-αt
の
像関数
は,次のようになります.
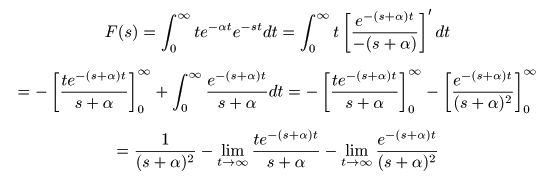
- ここで,
Re(s) = σ > -α
のとき,上式の第2項以降がすべて
0
に収束するので,
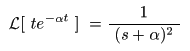
- となります.なお,
収束域
は
σ > -α
,
σ = -α
が
2位の極
となります.
- ここで,
α = 0
とおくと,
例題8
の結果に一致します.
[例題12] f (t) = t cos (ωt) のラプラス変換
- オイラーの公式
を用いて,
f (t) = t cos (ωt)
の
像関数
F (s)
は,次のように求められます.
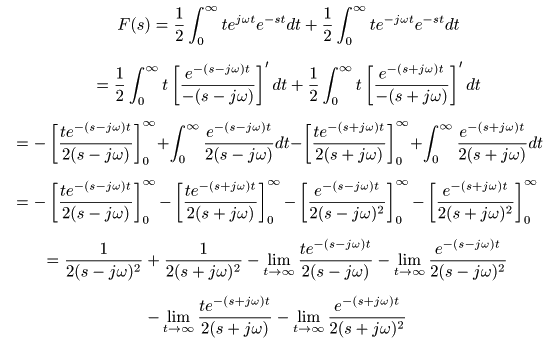
- ここで,
Re(s) = σ > 0
のとき,上式の第3項以降がすべて
0
に収束するので,
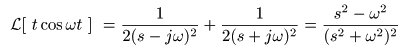
- が得られます.なお,
収束域
は
σ > 0
,
s = ±jω
が
2位の極
となります.
- ここで,
ω = 0
とおくと,
例題8
の結果に一致します.
[例題13] f (t) = t sin (ωt) のラプラス変換
- 同様にして,
f (t) = t sin (ωt)
の
像関数
F (s)
は,次のようになります.
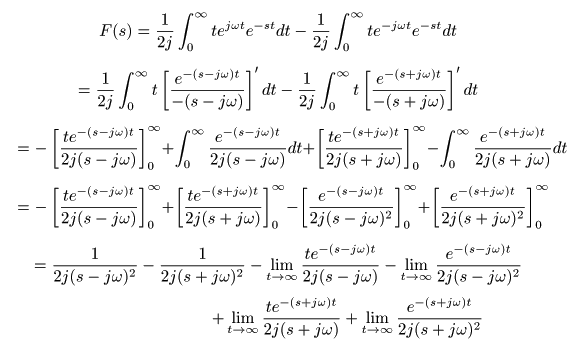
- ここで,
Re(s) = σ > 0
のとき,上式の第3項以降がすべて
0
に収束するので,
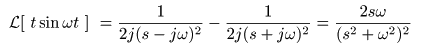
- が得られます.なお,
収束域
は
σ > 0
,
s = ±jω
が
2位の極
となります.
[例題14] f (t) = t e-αt cos (ωt) のラプラス変換
- オイラーの公式
を用いて,
f (t) = t e-αt cos (ωt)
の
像関数
F (s)
は,次のようになります.
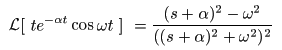
- なお,
収束域
は
σ > -α
,
s = -α±jω
が
2位の極
となります.
- ここで,
ω = 0
とおくと
例題11
,
α = 0
とおくと
例題12
の結果に一致します.
[例題15] f (t) = t e-αt sin (ωt) のラプラス変換
- 例題14
と同様にして,
f (t) = t e-αt sin (ωt)
の
像関数
F (s)
は,次のようになります.
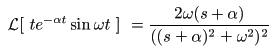
- なお,
収束域
は
σ > -α
,
s = -α±jω
が
2位の極
となります.
- ここで,
α = 0
とおくと
例題13
の結果に一致します.
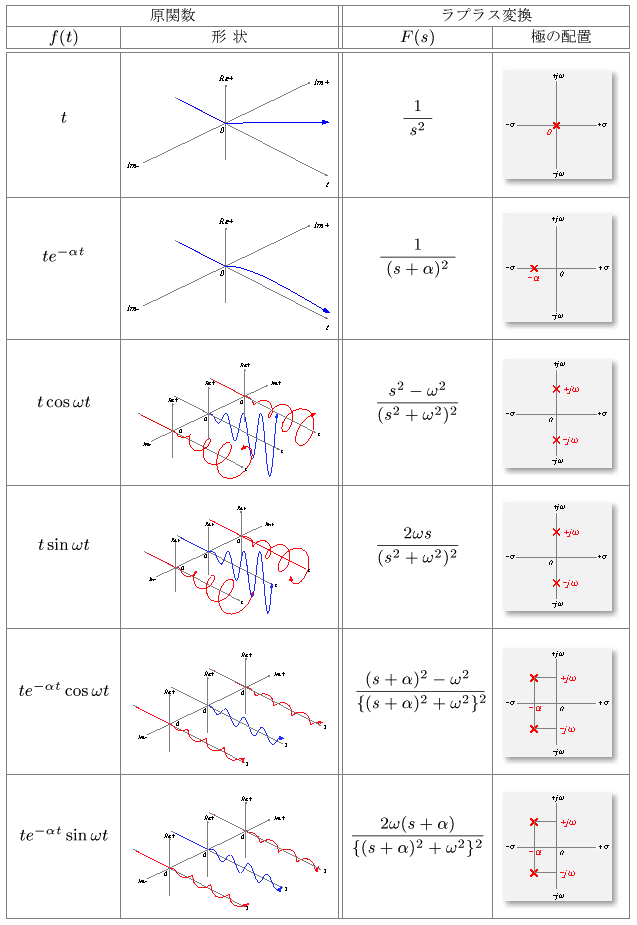
3.6 基本的な関数のラプラス変換
- 基本的な
ラプラス変換
の
対応関係
を,次の表に示します.
- なお,これらの
像関数
はいずれも
2位の極
をもっています.
[補足] 逆ラプラス変換とグルサの定理について
- ここでは,像関数
F (s)
が
n
位の極
をもつとき,その
逆ラプラス変換
は
グルサの定理
において,
- g (s)
を
指数関数
とした場合に一致することを示します.
- これにより,
逆ラプラス変換
における
ブロムウィッチ積分
の
直線的な積分路
を,
- より自由度のある
周回積分
C
に変更できることが保証されます.
- はじめに
コーシーの積分定理
を拡張した
グルサの定理
を示します.
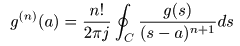
- この式で,
g (s)
は
領域
D
において
正則
となる任意の複素関数であり,
- a
は
領域
D
における任意の点,
積分路
の
C
は
領域
D
内にあって,
- 点
a
を正方向に1周する
単一閉曲線
とします.
- 例えば
n = 1
のとき,
グルサの定理
は次のようになります.
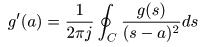
- これは,以下の
テイラー級数
から導くことができます.
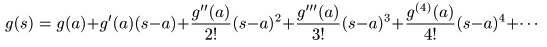
- この式を
グルサの定理
の右辺に代入します.
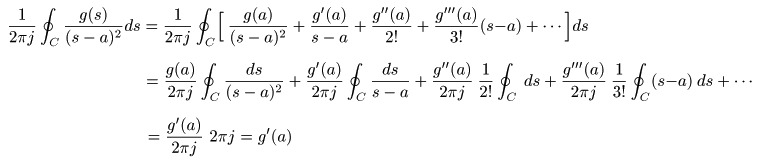
- ここで,
1 / (s - a)
の
周回積分
は
2πj
となりますが,他の項はすべて
0
となることを用いています.
- 次に,
g (s)
を次の
指数関数
とします.
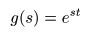
- このとき
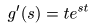
- より,
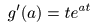
- が成立し,最終的に
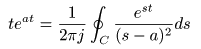
- が導かれます.ここで,
a
を
-a
に置き換えると,
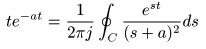
- となり,さらに
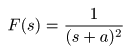
- とおくと,
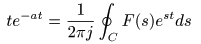
- が成立し,右辺は
積分路
を除くと
逆ラプラス変換
の式に一致します.
- これより,
2位
の極をもつ
像関数
の
1 / (s + a)2
と,
原関数
の
t e-at
が,1対1に対応することが分かります.
- 同様にして,
(n+1)位
の極をもつ
像関数
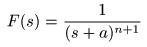
- について,
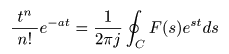
- が得られることは明らかです.
[参考] 積分値の発散と特異点の位数について
- フーリエ級数
では,
積分範囲
が
-∞
から
+∞
となっているので,
発散の問題
が
常に付きまといます.
- そこで,この
発散
を
回避
する手法が重要となり,
対象する
関数
f(t)
の
絶対値の積分
が
- 有限
となる
「
絶対可積分
」の条件を付加したり,
δ関数
をはじめとする
超関数
を導入する必要がありました.
- 一方の
ラプラス変換
では,
発散の様相
がその
像関数
F(s)
の表現に直接的に反映されています.
- 以下,具体的な事例を用いて補足しましょう.
- 一言で「
発散
」と表現しますが,
その状況は必ずしも一様ではありません.
- 例えば
原関数
f(t) = eαt
のとき,その
ラプラス変換
F(s)
は以下のようになります.
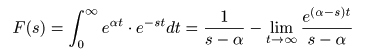
- ここで
s=α
は
孤立特異点
であり,
(
sの実部
)
>
(
αの実部
)
のとき,右辺の第2項は
0
に
収束
します.
- なお,
e (α - s) t
の値は,
s=α
において一定の値
1
になり,
- 時間
t
で
0
から
∞
まで
積分
するので,当然のことながら
発散
します.
- これらの操作は,
発散
や
収束
を伴う
回転
eα t
を
静止
させて観測するプロセスに他なりません.
- ここで,
f (t) = tn eα t
として,
s = α
を代入すると,
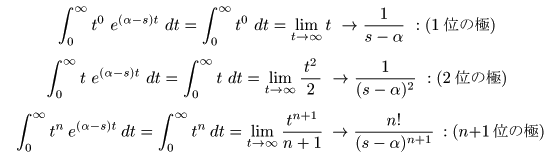
- のように
いずれも発散
しますが,その
速度
は
次数
n
につれて
大きく
なります.
- その影響は,
分母
(s-α)
の
指数
,すなわち
孤立特異点
s =α
の
位数
(n+1)
に表れています.
- 一方,
f (t) = eα t
の
像関数
F(s)
の第2項は,
(
sの実部
)
<
(
αの実部
)
のとき
発散
しますが,
- 解析接続
の処理で除去されることになり,それらの影響が
像関数
F(s)
に反映されることはありません.
- 以上をまとめると,
A i
,
s i
を任意の
複素数
,
n i
を
非負の整数
(0,1,2,…)
として,
- 対象とする関数
f (t)
を,以下のような
単純な関数
の
重ね合わせ
で表せるとき,
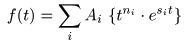
- ラプラス変換
の
線形性
により,その
像関数
F (s)
は以下のように求められます.
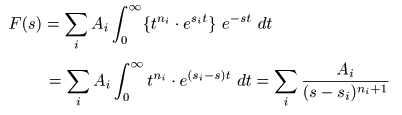
- すなわち,
ラプラス変換
は
e (si - s) t
の項が
時間
t
によらず
定数
1
となり,
その
積分値
が
- 発散
するような
s
平面上
の
孤立特異点
s i
を用いて,
その
位数
が
(n i +1)
となる
写像
を
- 行っている
ことが分かります.
4.ラプラス変換の目的とは?
- 本節では,
ラプラス変換
の真のねらい,その効用について説明します.
4.1 畳み込み積分とラプラス変換
- ここでは,
畳み込み積分
の式を
極めて単純な
変換の積
の形に変形させるためには,
- 積分変換
という操作が必要となり,最終的に
フーリエ変換
と
ラプラス変換
が導かれることを示します.
- 8 章の
線形システム
で説明したように,
入力
を
x (t)
,システムの
インパルス応答
を
h (t)
とおくと,
- 出力
y (t)
は,次の
畳み込み積分
の形で表されます.
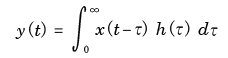
- この
畳み込み積分
の式が表す内容は極めて
単純
かつ
直観的
ではありますが,
- この式では,毎回
積分
の値を評価する必要があり,
扱いが極めて煩雑になります.
- もし,
入力
と,システムの特性を表す
伝達関数
との
積
の形で
出力
が表現できれば,
- 計算が飛躍的に
単純化
され,システムの挙動を簡単な
四則演算
により解析することが可能となります.
- そこで
畳み込み積分
の式に,下の図に示すような
変換操作
を加えます.
- すなわち,左側から
A
を,右から
B
,
C
の順に,ある操作を
加えます.
- ここで,記号の
A
,
B
,
C
の部分には,何らかの
数式
や
数学記号
が入ります.
- これから,この
A
,
B
,
C
の欄を埋めてゆきましょう.
- はじめに,
時間
τ
のみを含む
h (τ)
,
dτ
と,
積分記号
∫
を右側の
カッコ
内に移動します.
- なお,
B
は
B'
と
B''
の
積
の形に
変形
できるものとしています.
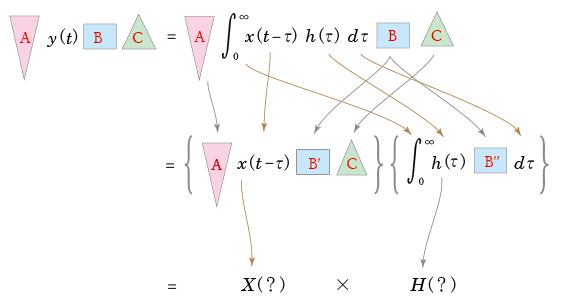
- ここで,
X (?)
と
H (?)
が
同形
になることから,記号
A
が
積分記号
であることは明らかです.
- 次に,左辺の
y (t)
を含む式の記号
C
は
dt
となることは容易に想像できると思います.
- なお,2行目の左側の
カッコ
の
C
は
d(t-τ)
となります.
- 例えば
t'= t-τ
おくと,
x (t-τ) = x (t')
と表せます.
- ここで,左の
カッコ
の中で
τ
を
一定値
とみなせば,
d(t-τ) = dt'
となることは明らかです.
- なお,
積分範囲
については,
t = 0
のとき
t' = -τ
,
t = ∞
のとき
t'= ∞
となるので,
- 入力
x
について,
t'< 0
のとき
x (t') = 0
という条件を満たせばよいことになります.
- これより,
積分範囲
はすべて
0 ~ ∞
となります.
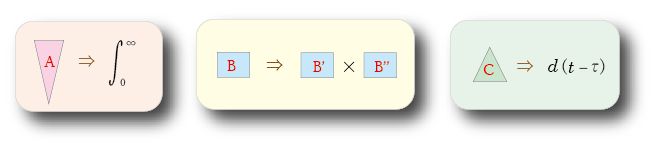
- 最後に,
B
および
B'
と
B''
の正体を明らかにしましょう.
- 積分変数から,
B
の変数は
時間
t
,
B'
は
t-τ
,
B''
は
τ
となります.
- したがって,記号の
B
を
関数
g (t)
で表すと,
- g (t) = g (t-τ) × g (τ)
- が成立し,
関数
の
積
が,
変数
では
和
の形になります.
- このような
性質
を持たすのは,
指数関数
です.
- そこで,
α
を任意の
複素数
として,
B
の操作を
g (t) = eαt
という
関数
に置き換えます.
- このとき,
α = -s
とおくと,この
積分変換
は以下に示すように
ラプラス変換
に一致します.
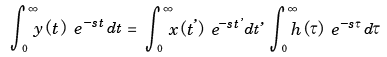
- すなわち,
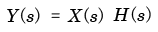
- また,
α = -jω
とおくと,
(片側)フーリエ変換
となります.
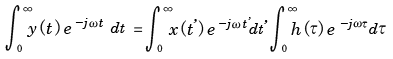
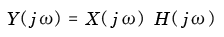
- このように,
畳み込み積分
を簡単な
積
の形に変換する操作は,
- フーリエ変換
と
ラプラス変換
だけであることが示されました.
- これを図で表すと,
以下のようになります.
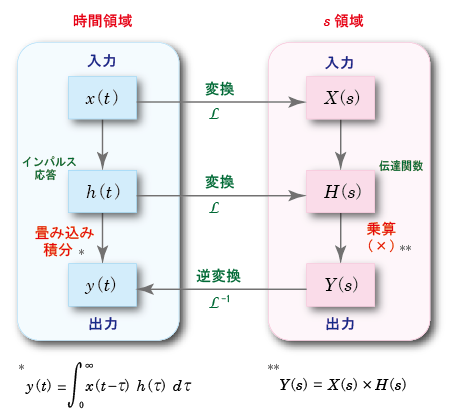
- すなわち,入力信号
x (t)
を
線形システム
に入力したときの出力信号
y (t)
は,
- インパルス応答
h (t)
と
x (t)
との
畳みこみ積分
の形で表現されます.
- 一方,
ラプラス変換
では,
変換
と
逆変換
の操作が必要になりますが,
- 右側の迂回路をたどることにより,複雑な
畳み込み積分
を用いることなく,
- 簡単な
乗算
により,
時間領域
の
出力
y (t)
を求めることができます.
- このように
ラプラス変換
は,いわゆる 「
急がば回れ!
」 の考えを具現化した手法と言えます.
4.2 像関数 F(s)の部分分数への展開
- 一般に,
像関数
の
F (s)
は,変数
s
の
有理式
の形になります.
- これを,簡単な
四則演算
により,極めてシンプルな
部分分数
の
和
の形に等価変形します.
- これにより,最終的な
出力
y (t)
を求める手法について説明します.
- 例えば,下の図のように複数の
線形システム
を何段も
縦続
に接続する場合について考えてみましょう.

- この場合,それぞれのステージの
インパルス応答
を
ラプラス変換
して得られる
伝達関数
Hi (s)
を
- かけ合わせることにより,
最終的な
出力
の
ラプラス変換
Y (s)
を求めることが可能です.
- この
Y (s)
を
逆ラプラス変換
することにより,
出力信号
y (t)
が定まります.
- なお,出力の
像関数
である
Y (s)
は,以下のように
s
を変数とする
有理式
の形になります.
- ここで
Y (s)
の分母が異なる
m
個の
根
をもつと仮定すると,
- それらは,
Y (s)
の
孤立特異点
となり,すべて
1位の極
となります.
- 次に,四則演算を用いて
s
の
有理式
Y (s)
を変形し,
m
個の
部分分数
の和の形に変形します.
- なお,それらの
部分分数
は,すべて
A / (s-α)
の形で表されることは明らかです.
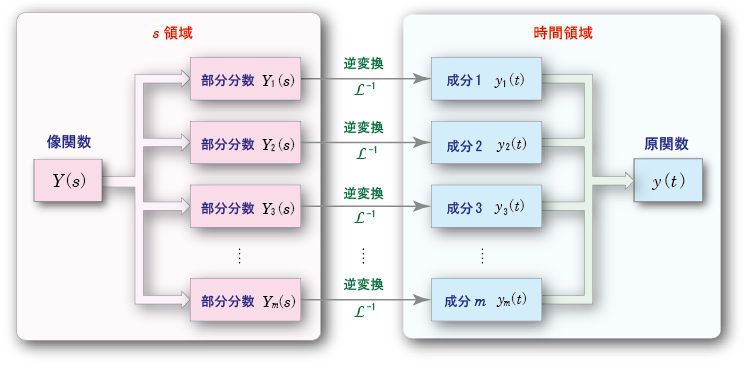
- 以上の操作は,
有理式
Y (s)
の
等価変換
とみなすことができますが,
- 先に述べた
逆ラプラス変換
における
極
と,それを巡る
積分路
の変更による
留数
の計算に等価です.
- 例えば,
s平面
上に
m
個の
1位の極
が配置されているとします.
- 先に,それぞれの
極
を
反時計方向
に1周する
積分路
を用いて求めた
留数
から,
- 対応する
原関数
yi (t)
の成分を求め,その総和を求める事例を示しましたが,
- 同じことを表しています.
- 先に述べたように,
像関数
Y (s)
の値は,
s平面
の
極
において
∞
に発散します.
- 値が
∞
となる極について,異なる
極
をもつ
像関数
による
有限
な成分が加算されたとしても,
- 本来の
極
の
位置
や,その
実質的な高さ
は微動だにしません.
- このような性質により,
像関数の形
がどれほど複雑であろうと,
- それを構成する
極
や
留数
の値を,正確に
分離・抽出
できるわけです.
4.3 ラプラス変換の微分則
- ここでは,
ラプラス変換
の
微分則
について検討します.
- 関数
f (t)
を時間微分した
f ' (t)
の
ラプラス変換
は,
- 部分積分
を用いると
次のように求められます.
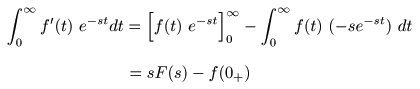
- すなわち,
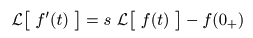
- が成立します.
- この式の右辺の第2項
- f (0 +)
は,
関数
f (t)
に含まれる
定数成分
の影響を
除去
するための項です.
- 例えば,先の
例題8
では,
1次関数
f (t) = t + C
の
ラプラス変換
が
F(s) = 1 / s2
であることを示しました.
- ここで
定数
の
C
がどのような値であっても,その
微分
は同じ結果になるはずです.
- すなわち,
左辺
は
C
に依存しません.
- 一方,
右辺
の
定数
C
の
ラプラス変換
は
C / s
となるので,
s
をかけると
+ C
となり,
- これを
打ち消すための
第2項
- f (0 +) = - C
が必要になるわけです.
- 1階微分と同様にして
f (t)
の
2 階微分
f '' (t)
の
ラプラス変換
は,
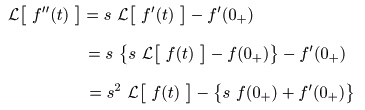
- となります.
- この式の
左辺
は
f (t)
の
2 階微分
が対象となるので,
f (t)
に含まれる
定数
のみならず,
- 1 階微分
により
定数
になる成分についても,これを打ち消す必要があり,
- - f'(0+)
の項が付加されています.
- このとき,
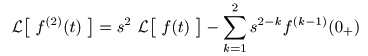
- のように表すことができるので,これを一般化すると,
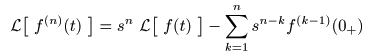
- が導かれます.
4.4 微分方程式のラプラス変換
- 次に,
微分方程式
の
ラプラス変換
について検討します.
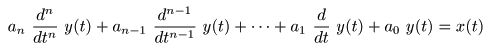
- この
微分方程式
を
ラプラス変換
すると,以下のようになります.
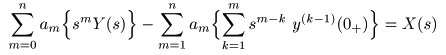
- ここで,
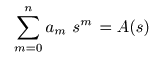
- さらに,
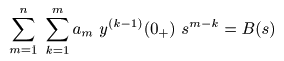
- とおくと,
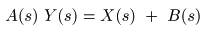
- となり,
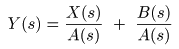
- が導かれます.これより
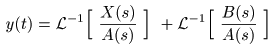
- が導かれました.
- なお,
Y (s)
は
変数
s
の
有理式
の形になるので,
四則演算
を用いて
- 部分分数の和
の形に変形することができます.
- 最終的には,
留数の定理
などを用いて,その解を求めることが可能です.
- 以下,その具体的な手法について説明します.
- an ≠ 0
が成立するとき
A(s)
は
変数
s
の
n
次式
となるので,
- 複素根
を含めると最大
n
個の
根
をもちます.
- なお,係数の
ai (i = n , n-1 ,‥, 0)
がすべて
実数
のとき,
- 実根
と
複素共役
の関係にある
2つの根のペア
から構成されます.
- A(s)
の
n
個の根が
重根
を含まないとき,必然的に
- Y(s)
は
n
個の
1位の極
をもつことになるので,
これらを
α0 , α1 ,‥,αn-1
とすると,
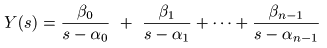
- のように表すことができます.
- ここで,
分子の係数
β0 , β1 ,‥, βn-1
はそれぞれの項の
留数
に相当するので,
- 先に
留数
の項で説明したように,
以下の式が成立します.
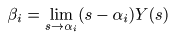
- この式を用いることにより,
煩雑な式の変形操作を行うことなく,
-
簡単に
Y(s)
を
部分分数の和
の形に変換することが可能です.
[参考] 最も単純な微分方程式を解いてみる
- これまで,
ラプラス変換のイメージ
や,
その応用としての
微分方程式の解法
等について示してきましたが,
- ここでは
最も単純な微分方程式
を例に,その
具体的な解
を求めてみましょう.
- イメージ
が湧きやすいよう,
簡単な運動の例
を以下の図に示します.
- ここで,
壁の位置
を
原点
として
水平方向
に
x軸
を設定し,
x = 5 [ m ]
の位置から
壁
に向かって
- 左方向
に歩きます.
-
壁の位置
でぴたっと
静止
するためには,
距離
x
の値に応じて
接近速度
v
を小さく抑える必要があります.
- 例えば,
距離
x
に
比例
するようにその
速度
v
を制御すれば,
近づくほど
速度
を小さく抑えることができます.
- このとき,
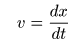
- であり,
速度
が
負の左方向
を向いていることから,
正の実数
a
を用いて,
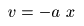
- と表すことができます.ここで上式を代入すると,
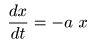
- が得られ,
変数
が
x
と
t
の
微分方程式
になっています.
- この場合,以下に示すように左辺は
変数
の
x
のみ,
右辺は
t
のみの式に
変形
することができ,
- 変数分離形
と呼ばれます.
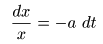
- これより両辺を
時間
0
から
t
まで
積分
すると,
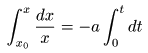
- となります.
- ここで
x0
は
t = 0
における
変数
x
の
初期値
(5m)
であり,実際に
積分操作
を行うと,
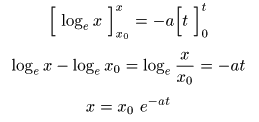
- が得られます.実際に
上式
を
t
で
微分
すると,
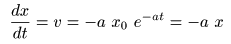
- となります.
- このように,
位置
x
とそれを
時間
t
で
微分
した
速度
v
の間に
比例関係
が成立するとき,
- その解は
指数関数
の形になり,
時間
t
の係数は,その
比例定数
に等しくなります.
- なお,図では,
比例係数
-a = -0.2
における
x (t)
と
v (t)
の波形を表していますが,
- その値を変更することができますので試してみて下さい.
- 次に,同じ
微分方程式
を
ラプラス変換
を用いて解いてみましょう.
- 距離
x (t)
の
ラプラス変換
を
X (s)
とし,先で示した
ラプラス変換の微分則
を適用すると,
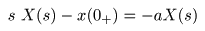
- が得られます.ここで
x (0+)
は
x (t)
の
初期値
(5m)
であり,変形すると,
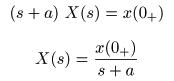
- となります.これを
逆ラプラス変換
すると,
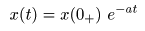
- となり,当然のことながら先ほどと
同じ結果
が得られています.
[補足] RCL回路素子の動作を可視化すると
- 電子回路
の
動的な特性
を解析する手法として,しばしば
ラプラス変換
が用いられます.
- 後ほどその
事例
を紹介しますが,
ここではそのための
準備
を行います.
- 回路
を構成する
要素部品
は,大きく
抵抗
をはじめとする
受動素子
と,
トランジスタ
- を代表とする
能動素子
に分類できますが,
ここでは,基本的な
受動素子
から,
- 抵抗
R
,
コンデンサ
C
(キャパシタンス)
,
コイル
L
(インダクタンス)
を取り上げます.
- これらの
電子回路の動作
は目に見えないので,その
働き
を具体的に
イメージ
することは
- 容易ではありませんが,
ここでは
電界
における
電子の動き
を,
重力場
における
- 水の流れ
に置き換えることにより,その
可視化
を試みます.
- はじめに,
抵抗
R
の例から始めましょう.
- 下の図に示すように,
2つの水槽
をつなぐ
ホース
(
パイプ
)に
水
が流れています.
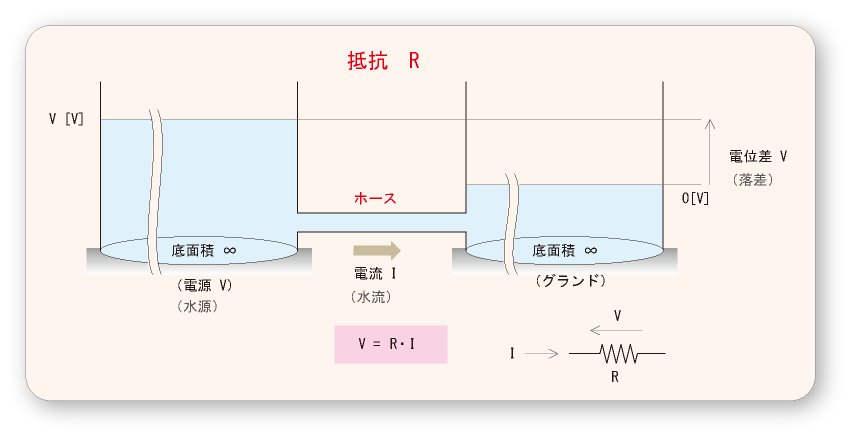
- 水
は
高い方
から
低い方
へ,すなわち
右方向
に流れますが,この
水流の量
I
は
落差
V
に
- 比例
することは容易に想像できると思います.
- すなわち,
比例定数
を
R
として
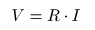
- となり,いわゆる
オームの法則
が成立します.
- 水
は
非圧縮性
の液体なので,水路に
分岐
がない限り
断面
を
単位時間
に流れる
水量
I
は,
- 水路の
いずれの部分
でも
同じ値
になります.
- また,
ホース
を
2本
に増やせば
全体の流量
I
は
2倍
になり,ホース2本を
縦に接続
して
- その
長さ
を
2倍
に延長すると,
流量
I
は
半分に低下
することが容易に想像できると思います.
- これより
落差が一定
のとき,
流量
の値
I
はホースの
断面積に比例
し,
長さに反比例
するものと考えられます.
- 一方の
電子回路
では,
プラスの電荷
は
電界
という場で
マイナス
の方向に引き寄せられますが,
- これは
重力場
の中で
質量
のある水が下の方向に
落下
することと等価です.
- これより,
水
は
電荷
に,
水圧
(
水位
)
は
電圧
に,
水の流量
は
電流
に読み替えられることは明らかです.
- 次は,
コンデンサ
の働きを
可視化
してみましょう.
- コンデンサ
(
キャパシタンス
)
は,下の図に示すように,
底面積
が
C
の
容器
に例えることができます.
- この
C
は
コンデンサの容量
に対応します.
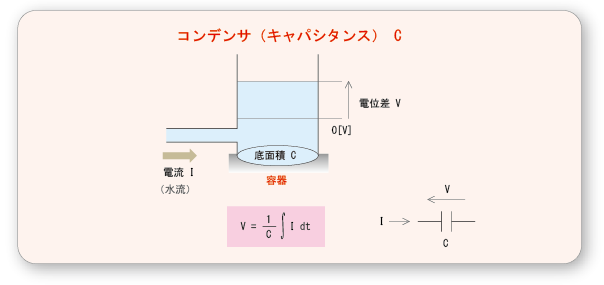
- 左からこの
容器
に
I
[リットル/秒]
の水が流れ込んでくるとき,これを
時間
t
で
積分
した
- 水の
総量
Q
を
底面積
C
で割った値が,
容器の
水位
V
に対応します.すなわち,
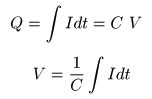
- が成立します.なお,
水位
(
高さ
)
を計測するには
基準
が必要となるので,
- 例えば
海抜
0 [m]
のような
グランドレベル
0 [V]
を定める必要があります.
- 一方,容器から
外部
に向かって水が
流出
する場合,
「
容器が空になってしまうのでは?
」という
- 疑念が生じますが,
電荷
には
プラス
と
マイナス
の両方があるので,問題は生じません.
- すなわち,
底なしの容器
を用いていると考えればよいでしょう.
- また,先に示した
抵抗
の図において,
2つの容器
を使用しています.
- これらの容器では
ホース
を介して水が
出入り
しますが,
底面積
が
∞
のため容器と水面の
- 相対位置
は変わりません.
- すなわち,電圧が一定の
電源
や
グランド
とみなすことができます.
- 最後に,
コイル
L
の働きについて考えてみましょう.
- コイル
(
インダクタンス
)は,次の図に示すように,
フライホイール
(
はずみ車
)のついた
- 水車
(
ポンプ
)に例えることができます.
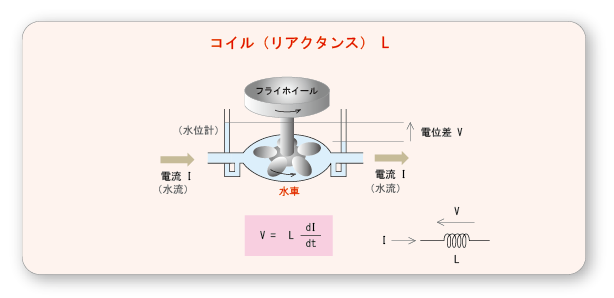
- なお,
水車の両端
には,入口と出口における
圧力
を計測するため,
上端
が外気にさらされた
- 透明な
パイプ
(
水位計
)が付属しています.
- 水車はその
慣性力
のため,流量の
変化を妨げる
ような働きをします.
- 例えば,
流量が一定
のとき十分な時間を経過した後,
水車の回転数
も一定になり,
- その両端の
水位差
は
0
になります.
- このとき,
水車のブレード
と
水
との間に
相互作用
はなく,
流れに影響を与えることはないので
- 両端の水位
は
同じ高さ
を示します.
- 流量
I
が
増加傾向
にあるとき,水車の
回転数
は徐々に
上昇
しますが,
- 慣性
による
遅延
が生じます.
- すなわち,その時点の
流量
I
にふさわしい
回転数
には達していないので,
- 流れの
入力側
では,水車のブレードの進行方向と
反対の面
に,
- 回転を
加速
しようとする
高めの圧力
が発生します.
- 他方の
出力側
では,ブレードの
進行方向の面
に,これをこれを吸い寄せようとする
低めの圧力
が加わるので,
- 入力側
(
左端
)の水位が
出力側
(
右端
)より高くなります.
- 一方,流量
I
が
減少傾向
にあるとき,水車の回転に
ブレーキ
をかける方向の圧力
が発生します.
- すなわち,
入力側
ではブレードの進行方向と
反対の面
に,これを吸い寄せようとする
低めの圧力
が,
- 出力側
では,
ブレードの
進行方向の面
に,これを押し留めようとする
高めの圧力
が加わります.
- このため,
出力側
(
右端
)の水位が
入力側
(
左端
)より高くなります.
- このように,
水位計の差分
V
は
流量
I
の
時間的変化
に比例する値を示し,
- その
比例係数
L
を
インダクタンス
と称します.すなわち,
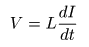
- が成立し,フライホイールが
重く
なるほど
インダクタンス
L
の値は
増加
します.
- このような
水車
を用いた説明は,
ホース
や
容器
の場合に比べ,
- イメージすることが難しいかもしれませんが,
参考になればと思います.
[参考] RC回路における放電現象について
- 先に,最も単純な
微分方程式
の例として,壁までの
距離
x
に
比例
した
速度
v
で接近する事例を紹介しましたが,
- これに
等価
な現象は,
電子回路
や
流体力学
をはじめとする様々な領域・分野で見受けられます.
- ここでは,
抵抗
と
コンデンサ
を組み合わせた
電子回路
の動作について検討します.
- 次の図は,
抵抗
R
と
コンデンサ
C
を
直列
に接続した回路の
放電現象
を表しています.
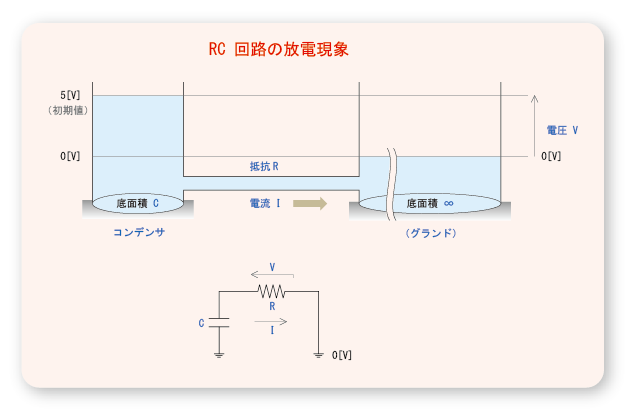
- 電子回路の可視化
の項で,
抵抗
R
の動作イメージを示しましたが,上図では
左側の容器
が
- 底面積
∞
の電源ではなく,
有限
な
底面積
C
をもつ
コンデンサ
に変わっている点に注意が必要です.
- 水は
高い方
から
低い方
に流れることに変わりはありませんが,
限られた底面積
をもつ容器の場合,
- 水の
流出
によりその水位は
下がる
ので,容器との
相対的な位置関係
は絶えず変化します.
- オームの法則
により,
抵抗
R
(ホース)には
電位差
V
(水の落差)に比例した
電流
I
(水流)が流れます.
- なお,左側の容器の
断面積
C
は
一定
なので,水面が下がる
速度
に
底面積
をかけたものが
電流
(水流)に相当します.
- このとき
電荷
(水の量)を
Q
として,以下の式が成立します.
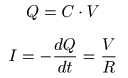
- ここで,
最初の式
を次の式に代入すると,以下の
微分方程式
が得られます.
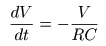
- すなわち,
電圧
V
を
時間
t
で
微分
すると,
-1/RC
倍されることになり,
- 先に示した
微分方程式
の
係数
a
に,
RC
(時定数)
を代入した形になっています.
- これより,
位置
x
の
初期値
x0
(= 5 [m])の代わりに,
電圧
V
の
初期値
V0
(= 5 [V])を用いて,
- 次の
指数関数
の解が求められます.
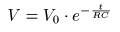
- すなわち,
時間
t
の経過につれ
電圧
V
は右側の
電圧
0 [V]
に接近し,
- コンデンサ
に蓄積された
電荷
Q
も徐々に
放電
され,最終的には
0 [C]
になります.
[補足] RC回路のステップ応答
- 先の
RC回路
では,
電源
を含めすべての容器は
固定
されていましたが,ここでは
- 下の図に示すように,
初期値
として
コンデンサの電位
(電荷)を設定する代わりに,
- 左側の容器
(電源)の
位置
を
変化
させることを考えます.
- 例えば,
左側
の容器(電源,グランド)の
位置を上下
させると,
右側
の容器の水位は
- これと
同じ高さ
になるよう追随します.
- 逆に,
右側
の容器の位置を
上下
させると,その水位は
左側
の容器の水位(一定値)に
- 復帰
しようとします.
- これらは,一見すると
異なる現象
のように見えますが,実はその
落差
が
0
になるよう
- 水が
2つの容器
の間を移動しているに過ぎず,
一つの現象
を
異なる視点
から
- 観測していることに他なりません.
- すなわち,容器の
相対的な位置関係
が同じであれば,
いずれの容器
を動かしたとしても,
- 計測する基準
が変化しただけであり,
同じ現象
が起きていることになります.
- なお,
抵抗
R
については問題は生じませんが,実際に
ホース
(パイプ)を使用する場合,
- 断面積
や
長さ
等の特性を変えることなく,
上下方向の動き
に対しゴムのように
- フレキシブルに
追随
する必要があります.
- さらに,上下に移動する
左の容器
には,その
位置
(電圧)を計測するための
基準点
が
- 必要になるので,
静止
して十分な時間が経過した後の
水位
(0m)
の位置に,
0[V]
の
- マーク
を
付ける必要があります.
- この
RC回路
では,新たに
入力信号
Vi (t)
が定義されており,
抵抗
R
の
左端子
に
- 接続されています.
- さらに,
コンデンサ
の下の端子は
グランド
(0 V)
に固定されており,
抵抗
R
との
- 接続点
が
出力信号
Vc (t)
になっています.
- ここで,
入力信号
Vi (t)
を
0 [V]
と
5 [V]
の間で
ステップ状
に遷移させて,
- 出力信号
Vc (t)
の変化を観測すると,図の波形のようになります.
- 特に,
入力
が
0 [V]
から一定の値(例えば
5 [V]
)に遷移したときの出力を,
ステップ応答
と呼びます.
- 以下,これらの
波形の変化
について詳しく眺めてみましょう.
- 例えば
入力信号
が
0 [V]
のとき,
右側
の
コンデンサ
も同じ
0 [V]
に向かって
放電
が進み,
- 十分な時間が経過すれば,これに接続する
出力信号
Vc (t)
は
0 [V]
に達します.
- 次に,
入力信号
が
0 [V]
から
5 [V]
に変化すると,
抵抗
R
を経由して
- コンデンサに
電荷
が蓄積され,
入力電圧
の
5 [V]
に向かって
充電
が進行します.
- これまでの
RC回路
では,グランドレベルの
0 [V]
に向かって,
放電
するケースについて
- 解析してきましたが,
先に述べたように,
5 [V]
に
充電
する場合についても,
- 観測する電圧の
基準
や
±
の
符号
が変わっただけであり,基本的にこれまでと同様,
- 指数関数
をベースとする電圧の変化を示します.
- ちなみに,
入力信号
Vi (t)
が
5 [V]
から
0 [V]
に変化する時点を
t = 0
とすると,
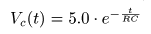
- の形になっており,
この式は,先に求めた結果に一致します.
- なお,
抵抗
R
と
コンデンサ容量
C
の積を
時定数
と呼び,この値が大きくなるほど,
- 充放電
の速度は
遅く
なります.
- 図中の
R
と
C
のボタンを操作することにより,
それらの値を
増減
することができますので,
- RC回路
の挙動が具体的にイメージできるよう確認して下さい.
[補足] 線形システムの入出力信号と伝達関数
- 先ほど
ステップ応答
を求めた
RC回路
において,
出力側
に接続する計測機器等の
- 入力インピーダンス
が十分
高く,
電流
が外部に
流出しない
場合,
抵抗
R
に流れる
- 電流
I (t)
は,
すべて
コンデンサ
C
に流れ込むことになります.
- このとき,
電流
I (t)
について以下の式が成立します.
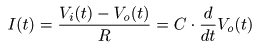
- 次に,この式を
ラプラス変換
します.
入出力信号
Vi (t)
,
Vo (t)
の
ラプラス変換
を
- それぞれ
Vi (s)
,
Vo (s)
とおくと,
微分則
を適用して,
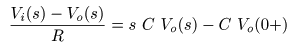
- が導かれます.ここで,
Vo (0 +)
は
出力信号
Vo (t)
の
初期値
であり,
- 左辺の
Vo (s)
の項を
右辺
に移動すると,
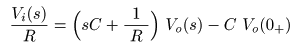
- のようになります.ここで,
初期値
の
Vo (0 +)
が
0
のとき,
入出力
の比は,
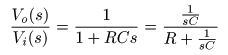
- のように求められます.この式の
右辺
を
G (s)
とおくと,
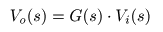
- となり,
G (s)
をこの
RC回路
の
伝達関数
と呼びます.
- ここで,
電流
I (t)
の
ラプラス変換
を
I (s)
とおくと,上式から
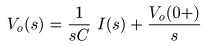
- となり,
1 / s C
は
抵抗
の
次元
[Ω]
をもつことが分かります.
- ここで,以下の図に示すように,
2つの抵抗
R 1
,
R 2
を
直列
に接続した回路を用いて,
- その
入出力
の関係について整理してみましょう.
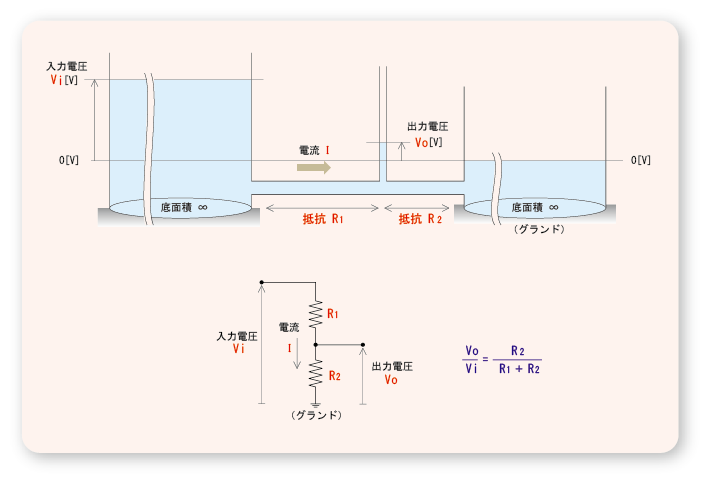
- 2つの抵抗
には
同じ電流
が流れるため,電圧に関する
分配則
が成立し,
入力
と
出力
の
比
は,
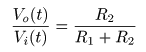
- のようになります.また,これを
ラプラス変換
した場合も,
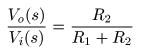
- のように
同じ関係式
が成立します.
- なお,
R 1
と
R 2
が等しいとき,
出力電圧
V o
は
入力電圧
V i
の
1 / 2
になることは明らかです.
- さらに,
R 2
に比べ
R 1
の値が小さくなると,
出力電圧
V o
は
入力電圧
V i
に近づき,
- さらに,逆に
R 2
が小さくなると,
0 [V]
に接近します.
- ここで,先ほど検討した
RC回路
において,
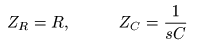
- とおくと,その
伝達関数
は,
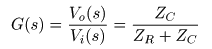
- のようになり,基本的に
2つの抵抗
R 1
,
R 2
を用いた場合と
同形
になっていることが分かります.
- ここで,上記
Z R
と
Z C
はいずれも
抵抗の次元
[Ω]
をもち,それぞれ,
抵抗
および
コンデンサ
の
- 複素インピーダンス
と呼ばれます.
- なお,
コンデンサ
の場合,その両端に発生する電圧は,
電流
I
を
積分
したものに
比例
するので,
- 変数
の
s
が
分母
に表れますが,
コイル
(
インダクタンス
)の場合は,
電流
I
を
微分
したものに
- 比例
するので,
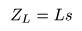
- のように表わされます.
- ここで,
入力信号
Vi (t)
に,高さ
v0
の
ステップ状の信号
が入力されたとき,
ユニット関数
u (t)
を用いて,
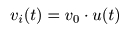
- のようになります.これを
ラプラス変換
すると,
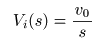
- となるので,最終的に
出力信号
は
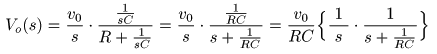
- のような
乗算
の形になり,これが
RC回路
の
ステップ応答
を表しています.
[補足] ステップ入力と伝達関数の像関数
- ステップ入力
u (t)
の
ラプラス変換
1 / s
,
RC回路
本体の
伝達関数
に相当する
1 / (s + a)
,
- それらの
積
に対応する
像関数
(
実部
と
虚部
)の形状を,以下の図に示します.
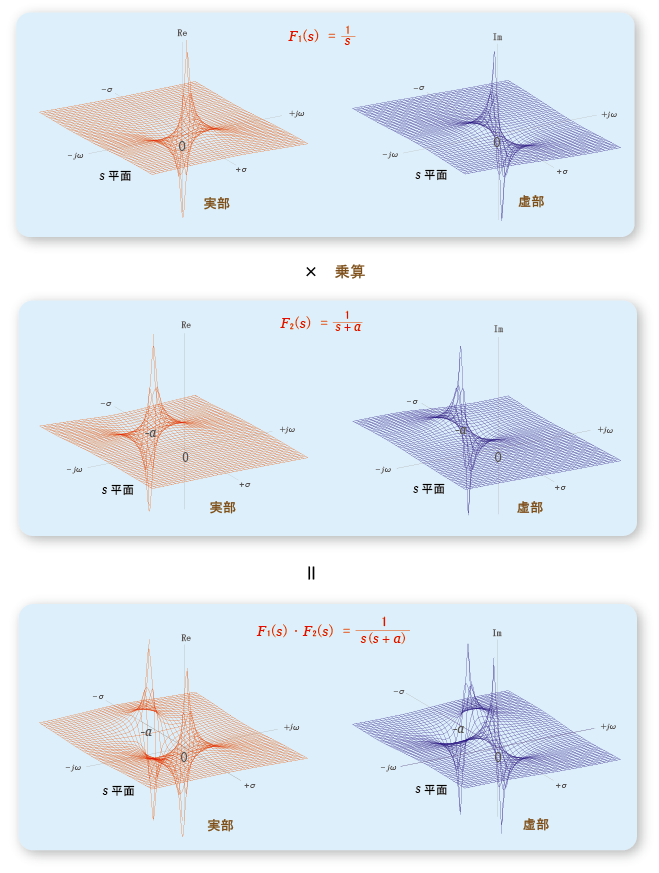
- 上の図は
入力信号
u (t)
の
像関数
1 / s
を示しており,
s = 0
に
1位の極
が現れています.
- 一方,
RC回路
の
伝達関数
G (s) = 1 / (s + a)
は,中央の図に示すように,
s = -a
に
1位の極
をもっています.
- これらの
積
1 / s(s+a)
は下の図に示すように,
s = 0
と
s = -a
に
2つの極
をもち,
- 上記と細部の形状は異なるものの,
入力信号
と
伝達関数
の
特異点(極)
はそのまま
- 保存
されていることが分かります.
- なお,これまでは
a ≠ 0
における
像関数
について検討してきましたが,
a = 0
の場合は
- s = 0
に
2位の極
をもつことに注意が必要です.
- ここで
注目
すべきは,
畳み込み積分
項で説明したように,
入力信号
のラプラス変換と,
- 線形システム
の
インパルス応答
のラプラス変換の
積
が,
出力信号
の
ラプラス変換
を表す点にあります.
- すなわち,これらの
像関数の積
が
線形システムの出力
という具体的な
物理量
を表現していることが,
- ラプラス変換
の
有用性
を飛躍的に高めたといえるでしょう.
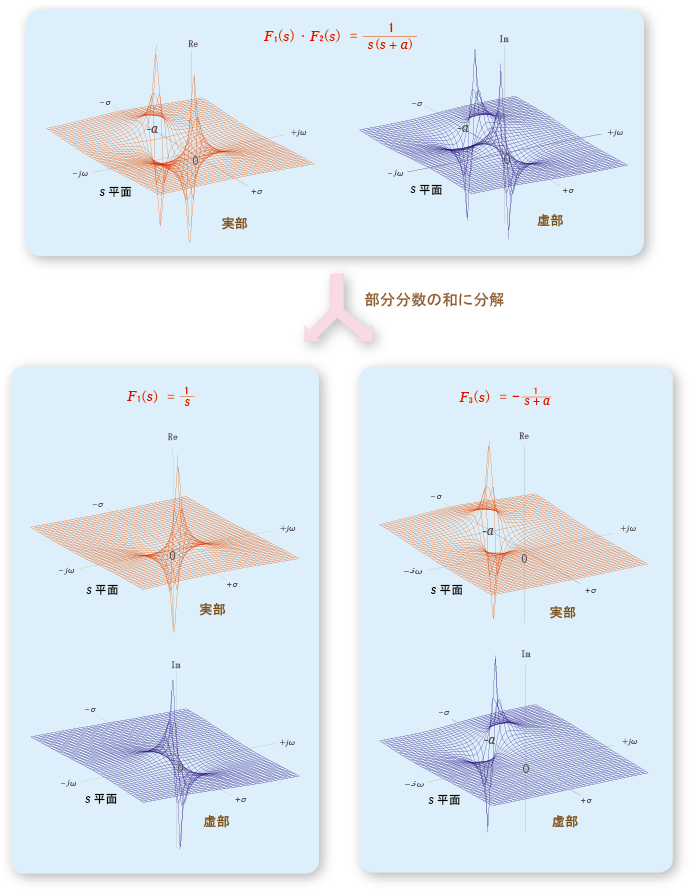
[補足] 複数の極をもつ像関数を部分分数の和に分解する
- これまで,
RC回路
の
ステップ応答
について計算を進めてきましたが,
- 下の図に示すように,その
出力信号
を表す
像関数
1 / s (s + a)
には,
0
と
- a
に
- 2つの極
が含まれているので,
これを直接
逆ラプラス変換
することはできません.
- そこでこの
像関数
を,それぞれ
単一の極
をもつ,より
シンプル
な
像関数
の
和
の形に
分解
します.
- 具体的には,その
像関数
の
分母
が,
s (s + a)
のように
乗算
の形になっているので,
- 下の図に示すように,
分母
が,
s
および
(s + a)
となる
部分分数の和
に分解します.
- 以下,
具体的な手順
を示しましょう.
- 求める
RC回路
の
出力
Vo (s)
が,
変数
A
,
B
を用いて,
以下のように
1位の極
をもつ
- 2つの
像関数の和
の形に,
変形できるものと仮定します.
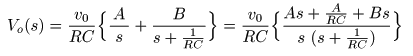
- ここで,
変数
の
A
,
B
は,以下の
2条件
を満たす必要があります.

- これらを解くと,
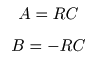
- のようになり,最終的に以下のような
解
が求まります.
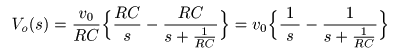
- なお,
変数
の
A
と
B
を用いないで,
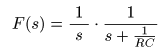
- とおき,
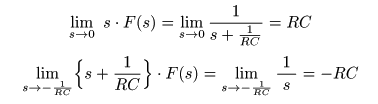
- を求めることにより,
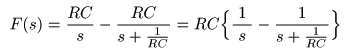
- のように,直接
部分分数
に分解することができます.
- ここで
出力
の
Vo (s)
を
逆ラプラス変換
すると,
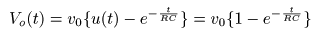
- が導かれます.
- すなわち,
出力信号
Vo (t)
は
時間
t = 0
で
0
であり,
目標値
の
v0
(5V)を目指して,
- 時定数
RC
の
指数関数
に沿って近づきます.
- なお,これを
時間
t
で
微分
すると,
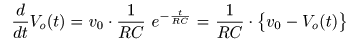
- のようになり,
接近の速度
は
電圧の落差
v0 - Vo (t)
に
比例
することが分かります.
- ここで,
分解後
の
像関数
F3 (s) = - 1 / (s + a)
は,
RC回路
の
伝達関数
F2 (s) = 1 / (s + a)
に
- 類似した形をしていますが,
±の符号
が
反転
しているので注意が必要です.
[補足] RL回路のステップ応答
- 抵抗
R
と
コイル
,すなわち
リアクタンス
L
を直列に接続した回路の
ステップ応答
について,下の図を用いて考えてみましょう.
- 例えば
入力信号
を
Vin(t)
,
出力信号
を
Vout(t)
,それらの
ラプラス変換
を,
Vin(s)
,
Vout(s)
とします.
- 抵抗
の
インピーダンス
は
R
となりますが,
コイル
,すなわち
リアクタンス
の
インピーダンス
は
sL
となるので,
- 入出力信号
の比率はその
分圧比
から以下のように表されます.
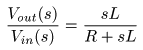
- ここで,
入力
Vin(t)
に,高さ
Vo[V]
のステップ状の
入力
を与えたときの
出力
Vout(t)
を求めます.
- 入力信号
Vin(t)
は
ユニット関数
u(t)
を用いて,
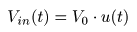
- のように表されるので,これを
ラプラス変換
すると,
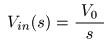
- が得られます.これより,
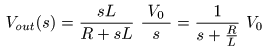
- のようになり,これを
逆ラプラス変換
すると,
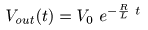
- が導かれます.
- 入力信号
の
Vin(t)
は,
時間
t = 0
において
0[V]
から
Vo[V]
に急峻に
変化
します.
- 出力信号
Vout(t)
も同様に
Vo[V]
に立ち上がりますが,その直後から
0[V]
に向かって
減衰
を開始します.
- この
減衰
は,最初は
速く
,徐々に
緩やか
になり,
その
速度
は
落差
Vout(t)
に
比例
するので
指数関数
の形になります.
- このとき,
L
の値が
小さい
ほど,
R
の値が
大きい
ほど,
減衰は速く
なり,
時間の次元
をもつ
L/R
は
時定数
と呼ばれます.
- 図の中央の
水の挙動
を用いて,このような変化を
イメージ
してみましょう.
- 抵抗
R
は
ホース
(
パイプ
),
リアクタンス
L
は
水車
に対応します.
- 時間
t = 0
で,入力となる左の
水槽の高さ
が
ステップ状
に変化すると,
ホース
を介して
水車の左側
に
圧力
が加わるため,
- 徐々にその
回転数
が
上昇
します.
- t = 0
の直後は,
水車
はほぼ
静止
しているので,
水車の水
は
流れ難い
状態にあります.
- このため,
出力電圧
に相当するホースとの
接続点の水位
は,左側の
Vo
に近い値になります.
- 時間の経過
につれ,水車の
回転
は徐々に
加速
され,回転数の
上限値
に向かって
漸近
してゆきます.
- ホースとの
接続点の水位
,すなわち
出力
がほぼ
0[V]
に
下がりきる
と,
水流の値
も
一定
になり,
- 水は
抵抗なく
水車を通り抜けます.
[参考] 伝達関数を用いたシステム解析における注意点
- ● 初期値の扱いについて
- 先に述べた,「
線形システムの入出力信号と伝達関数
」の項では,
RC回路
の
電流
に関する
微分方程式
を
- ラプラス変換
し,
入出力信号
の比を表す
伝達関数
から,最終的な
ステップ応答
を求める手法を示しました.
- この
伝達関数
を計算する段階では,
n
次の微分係数
を含む
すべての
変数
の
初期値
を
0
とみなしています.
- このように,
伝達関数
を用いた解析では,基本的に
すべての変数
が
静止
した状態を
初期値
としている点に
- 留意する必要があります.
- しかしながら,「
RC回路
の
放電現象
」の事例のように,
初期値
が
0
以外の値をとる場合については,
- 座標系
を適切に
設定
することにより,対処することが可能です.
- 例えば,
電圧の初期値
v0
(5V)を
原点
に,新たに
下向きの座標軸
Vnew
を設定すると,
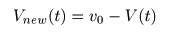
- が成立し,
t = 0
のとき
Vnew (0) = v0
となります.このとき,
V (t)
に上の
Vo (t)
の
解
を代入すると,
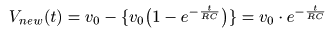
- となり,
初期値
v0
(5V)から
0 [V]
に向かって
減衰
する特性が得られます.
- なお,
新しい座標軸
Vnew
を採用しても,その
初速度
(
微分値
)は
0
となっている点に
変わりはありません.
- ● 線形システムの縦続接続について
- 先の
4.2
の項で述べたように,複数の
線形システム
を
縦続接続
する場合,その
出力信号
Y (s)
は,
- 入力信号
X (s)
に
それらの
伝達関数
G i (s)
を,段数分乗じたものになります.
- これらの関係は,
抽象的な数学
の領域ではそのまま成立しますが,
例えば
RC回路
や
水流
のような
- 物理量
を扱う
線形システム
に
適用
すると,
重大な誤り
を招くことがあります.
- 以下,その
理由
について説明します,
- 先に,
2つの抵抗
R 1
,
R 2
を
直列
に接続した回路を,
2つの
容器
を連結する
パイプ
により
- 表現した事例を紹介しましたが,その
入力
となる
左側
の
水槽
の
底面積
は
∞
で,
- どれだけ水が
流出
しようとも,その
水位
は変わりませんでした.
- すなわち,
入力信号
の
インピーダンス
(
内部抵抗
)は
0
とみなせました.
- 一方の
出力信号
は,
中央
の
細いパイプ
の
水位
に相当し,
わずかな水
が
流出
しても,
- その
高さ
が
変動
します.
- すなわち,
出力信号
の
インピーダンス
は,
2つの抵抗
を
並列接続
した値となり,
- 決して小さいとはいえません.
- このため,
複数
の
RC回路
を直接
接続
すると,それらの間に予期せぬ
電流
(水流)が流れ,
- その
電位
の様相が変わってしまいます.
- このような
入出力信号
の
相互作用
を避けるためには,
出力信号
に接続して,
- その
インピーダンス
が
0
とみなせる新たな
回路
を追加する必要があります.
- RC回路
の場合は,
出力インピーダンス
が十分
低く
,
利得
1
の
バッファーアンプ
を
- 挿入する必要があります.
5. まとめ
- 本章では,
ラプラス変換
の
物理的イメージ
を中心に解説しましたが,
- これらの概念を正確に捉えるためには,
複素関数論
の知識が必要になります.
- この
複素関数
の世界は,かの
高木貞治
先生が,その著書
解析概論
の中で,
- 「
驚嘆すべき朗らかさ!
」,「
玲瓏
(れいろう)
なる境地
」と表現されている数学の一分野です.
- 広辞苑によれば「
玲瓏
」とは「
うるわしく照りかがやくさま
」という意味です.
- それらを実感すべく,
以下の書籍などを
一読されてみてはいかがでしょうか?
- 高木貞治 定本 解析概論 岩波書店
- 神保道夫 複素関数入門(現代数学への入門) 岩波書店
- 井澤裕司 ビジュアル複素関数入門 プレアデス出版
-
⇒ ディジタル信号処理(基礎編)に戻る

