
ディジタルフィルタとz変換
井澤 裕司
1. ディジタルフィルタとは
- この章では、
「ディジタルフィルタとz変換」
について学習します。
- 信号の中から、特定の成分を取り出したり除去する回路や機能を
フィルタ
と言います。
- また、そのような処理や操作を
フィルタリング
と称します。
- コンピュータやDSP(Digital Signal Processer)を用いる場合は、離散値の信号を扱うので、必然的にディジタル
- フィルタとなります。
- このディジタルフィルタは、線形フィルタと非線形フィルタに分類されます。
- 本章で扱うのは線形のディジタルフィルタであり、これらは以下に示す基本的な構成要素で構成されます。
- (1) 遅延素子(1クロック)
- サンプリングの1周期(1クロック)だけ信号を遅延する素子であり、遅延を示す
D
を用いて表したり
、
- 後述するz変換の伝達関数を用いて
z-1
のように記述します。
- (2) 加算器
- 2つの入力信号
[ xn, yn]
に対して、その和
[ zn = xn+yn]
を出力する素子です。
- 減算を行う場合には、矢印の部分に符号の
-(マイナス)
を付け加えます。
- (3)乗算器(固定倍率)
- 任意の定数を
a
として、入力
[xn]
を定数倍
[ yn = a xn ]
して出力する素子です。
- この
a
の値が時間により変化する場合は、非線型フィルタとなります。
- 本章で解説するのは、固定倍率の線形フィルタです。

2. ディジタルフィルタの分類
- 線形のディジタルフィルタは、以下のように分類されます。
- (1)非再帰形ディジタルフィルタ(Non-recursive Filter)
- フィードバックのループがなく、インパルス応答は有限個のパルスで表されるので、有限インパルス応答
-
FIR
(Finite Impulse Responce)形とも呼びます。
- 簡単な非再帰形ディジタルフィルタの例を、下の図に示します。
- このフィルタは入力信号とこれを1クロック遅延された信号の平均値を出力します。
- 各構成要素の動作を理解して下さい。
- このフィルタの入出力の間には、次の関係が成立します。
- 一般化した非再帰形ディジタルフィルタの構成を下の図に示します。この形をトランスバーサル形と呼びます。

- このフィルタの伝達関数を求めてみましょう。上の図より以下の関係式が成立します。
- ここで1クロックの遅延素子の伝達関数を
z-1
で表すことができます。(詳細は後ほど説明します。)
- このとき、
xk-1 = z-1xk
が成立し、次のように書き改めることが可能です。
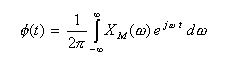
- すなわち、

- ここで、伝達関数
A(z)
は、次のように表せます。(詳細はz変換で説明します。)

- 証明を以下に示します。
- [証明]

- (∵ p<0 のとき xp=0より)
- このように、非再帰形フィルタの伝達関数は、zの多項式で表すことができます。
- なお、係数
ak
が有界な値をもつ限り、このフィルタは安定に動作し、出力の振幅値が発散するようなことはありません。
- (2)再帰形ディジタルフィルタ (Recursive Filter)
- フィードバックのループがあり、インパルス応答は無限に続くパルス列となるので、無限インパルス応答
- IIR
(Infinite Impulse Responce)形とも呼びます。
- 厳密には、フィードバックのループがあっても、インパルス応答が有限となる場合があります。
- すなわち、再帰形のFIRも存在します。
- 最も簡単な再帰形フィルタの例を以下に示します。乗算器の利得
a
を調整することができます。
- このフィルタは、利得
a
の値によりフィルタの利得が無限大となり、動作が不安定になります。
- 利得
a
をどのようにすると不安定になるか調べ、その原因を考察してください。
- この再帰形フィルタの特性を検討してみましょう。図より次の関係式が成立します。
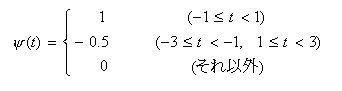
- これより、
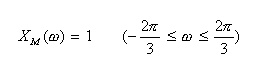
- フィルタの伝達関数は、次のようになります。
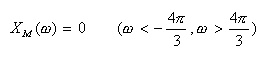
- ここで、z について
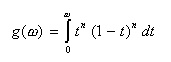
- すなわち、
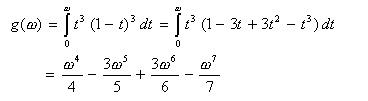
- が成立するとき、伝達関数の分母が0となり、フィルタの利得が∞となります。
- このような z=-a を
極(pole)
と呼び、フィルタの特性を決定する重要な要素です。
- 一般化した再帰形ディジタルフィルタの構成を次に示します。

- この再帰形フィルタの伝達関数
H(z)
を求めてみましょう。図より、以下の式が成立することがわかります。

- すなわち、

- これより、

- ここで、


- したがって、伝達関数
H(z)
は次のようになります。

- この伝達関数から、ディジタルフィルタの周波数特性を計算することができます。
3. z変換の定義
- ここでは、z変換について簡単に解説します。
- z変換の定義を示します。
- サンプル値列
{xn} ( n=0,1,2,‥)
が与えられたとき、
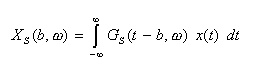
- を
{xn}
の
z変換
といいます。
- z変換とラプラス変換は密接な関係があります。
- その関係について説明しましょう。
- 例えば連続な入力信号
x(t) の
ラプラス変換
は次式で表されます。
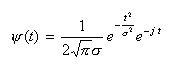
- ここで、
x(t)
をサンプリングした離散信号を
{xn}
とおくと、次の関係が成立します。
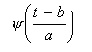
- これより、
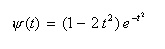
- と置くと、上式は
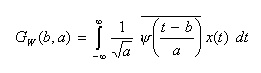
- のようになります。
- ちなみに1クロック(T)だけ信号を遅延する関数は
z-1
で表されます。
4. ディジタルフィルタの周波数特性
- ディジタルフィルタの特性を表現するのに、以下に示す2つの方法があります。
- (1) インパルス応答
- (2) 周波数応答
- 前章の「線形システム」では、インパルス応答をフーリエ変換したものが、そのシステムの伝達関数に
- なることを示しました。
- この概念を、以下の図に示します
- この周波数応答では、入力となる正弦波信号の周波数が連続的に変化するスウィ-プ信号として表現していますが、
- 厳密には単一の周波数を入力した場合の出力信号の振幅と位相を、周波数毎に求めたものです。
- ここで、ディジタルフィルタの伝達関数
H(z)
において、
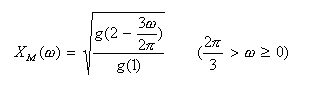
- と代入すると、このフィルタの周波数特性を求めることができます。
- これは、ラプラス変換において
s = jω=j 2πf
を代入して周波数特性を計算する過程に対応します。
5. 非再帰形ディジタルフィルタの周波数特性
- ここで、非再帰形フィルタの周波数特性について検討します。
- 先ほど述べたように、非再帰形フィルタの伝達関数は、zの多項式で表されます。
- たとえば、下の図のように
x0, x1, x2
という信号にそれぞれ
a0, a1, a2
という係数を掛けて加算した
- 3タップのフィルタを考えます。
- このフィルタの伝達関数
H(z)
は
- H(z) = a0 + a1z-1+ a2
z-2
- = a0 (α0 - z)( α1- z) / z2
- のように
因数分解
することが可能です。ここで、
z=α0
あるいは、
z=α1
のとき、伝達関数の値が0となることから
- ゼロ点(零点)
と言います。
- 3タップのフィルタではゼロ点は2つ存在し、図では
×
印で表しています。
- 係数
a0, a1, a2
の条件により、次の3つの場合が生じます。
-
(1)
[ a12 - 4a0 a2
> 0 ] のとき
⇒ 2つの実数
-
- (2)
[ a12 - 4a0a2
= 0 ] のとき
⇒ 1つの実数 (重根)
- (3)
[ a12 - 4a0a2
< 0 ] のとき
⇒ 2つの複素数 (共役複素数となる)
- このフィルタの周波数特性は、
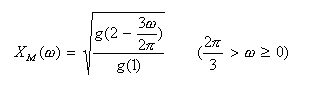
- を
H(z)
に代入して求められます。
- 上式は、z平面上の単位円上の点を表していることから、
単位円上にゼロ点
があると、その周波数での利得は0 となります。
- この利得の値は、単位円上の点と2つのゼロ点を結ぶ線分の長さの積に比例することは、上式から明らかです。
- この例は3タップのフィルタですが、一般的な非再帰形フィルタにおいても、そのゼロ点の位置をz平面上にプロット
- することにより、その周波数特性を直観的に表現することも可能です。
6. 再帰形ディジタルフィルタの周波数特性
- 次に、再帰形フィルタの周波数特性について検討しましょう。
- 先ほどの例で示した単純な再帰形フィルタの伝達関数は
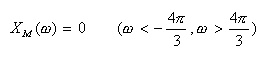
- で表されます。ここで
分母=0
となる z (すなわち、z=-a)を
極(pole)
と言います。
- この極をz平面では○
印で示します。
- この極が単位円上に存在すると、フィルタの利得は無限大となり不安定になります。
-
- 極の値を変化させて、フィルタの周波数特性がどのようになるか検討して下さい。
- a = 0
のとき零点と極が重なるため、これらは消滅することに注意して下さい。
- なお、このフィルタでは、ゼロ点と極がそれぞれ1つ存在します。
- 実数のパラメータ a を変化させると、極は実軸上を移動します。
- 一般的な再帰形フィルタでは、複数の極とゼロ点が存在し、極は複素平面上に配置されます。
- 実数のパラメータを用いた場合、極や零点は実数、あるいは共役複素数の対で現れます。
- 次に、2つのパラメータ a, b を有する2次の再帰型フィルタの例を示しましょう。
- フィルタの利得の値は、単位円上の点とゼロ点を結ぶ線分の長さに比例し、単位円上の点と極を結ぶ線分の長さに
- 反比例することは理解できると思います。
- ここで、一般的な再帰形フィルタの伝達関数
H(z)
を因数分解し、次のように表すことができます。

- ここで分子 = 0の根、すなわち

- が零点に相当します。
- また、分母 = 0の根、

- は極に対応します。
- このように、一般的な再帰形フィルタにおいて、その周波数特性は零点や極の位置と密接な関係があります。
- これらをz平面上にプロットすることにより、その特性を直観的に把握することが可能です。
7. ディジタルフィルタの安定性
- ディジタルフィルタにおいて、有界な入力信号について出力が常に有界となるとき、安定であると言います。
- この必要十分条件は、インパルス応答を
hk
(k=0,1,2,…)
としたとき

- あるいは、
- 「伝達関数
H(z)
の極がすべてz平面の単位円の内部にある」
- となります。
- したがって、有界な係数をもつFIRフィルタと非再帰形フィルタはすべて安定です。
8. 非再帰型ディジタルフィルタの設計手法
- 具体的なディジタルフィルタの設計手法には、様々な方式が提案されています。
- ここではその中から、フーリエ級数展開法を紹介しましょう。
- 非再帰型ディジタルフィルタの特性は、z変換を用いて次のように表されます。

- この式において、
z = ejωT
を代入し、その絶対値を計算すれば周波数特性が得られます。

- ここで、目標となるフィルタの周波数特性を
H0( ejωT)
で表します。
- 一般に、無限のタップ数を持つフィルタを用いれば、この目標となる特性を満たすことができます。
- しかし、現実には有限のタップ数でフィルタを実現しなければなりません。
- そこで、Nタップのフィルタ
H(ejωT)
と、目標となるフィルタ
H0( ejωT)
の差が最も小さくなるように、
- hk
を決定します。
- すなわち、

- とおいて、

- から、
hk
を計算すると、以下に示すフーリエ級数展開の形で解が得られます。

- 次に、この式を用いて実際に簡単なフィルタを設計してみましょう。
- ここでは、直線位相となる低域通過型(LPF)の非再帰型ディジタルフィルタを設計します。
- このフィルタのタップ係数は、中央タップについて左右対称となり、位相特性が直線的に変化するため、
- 処理した信号成分の重心点がずれないので、画像等のフィルタリングによく用いられます。
- 目標とするフィルタの周波数特性は、計算しやすいように、直流から
ωc
まで利得 1、
- それ以上で
0
となるものとします。 k≠0のとき、上式は次のようになります。

- なお、
h0
(k=0)は次式のようになります。

- この結果を、図を用いて表してみましょう。
- このフィルタは N=19、すなわちタップ数が19であり、中央のタップについて左右対称となっています。
- 図の上部にあるフィルタ特性のボタンをクリックすることにより、
低域通過型(LPF)
だけでなく、
- 高域通過型(HPF)
や
帯域通過型(BPF)
とすることも可能です。
- 目的とするフィルタの特性(
青
)は矩形状に変化していますが、設計したフィルタはタップ数が 19 と制限されているため、
- 周波数特性(
赤
)が波打っています。
- この変動成分は、信号を切り出した影響であり、
「Gibbsの現象」
と呼ばれています。
- (前章「離散フーリエ変換と窓関数」を参照のこと。)
- 窓関数を用いれば、周波数の分解能は低下しますが、この振動成分を押さえることができます。
- 窓関数(Window Function)を切り替えて、その効果を確認して下さい。
- なお、位相特性は直線状に変化し、出力信号は中央タップに対応する信号と同位相になっています。
- また、下のボタンを操作することにより、直接タップ係数を変更することができますので、周波数特性がどのように
- 変化するか試して下さい。
9. まとめ
- ディジタルフィルタとその特性について学習しました。さらに、フィルタの特性を評価する手法としてz変換を紹介しました。
- なお、z変換やフィルタ設計法の詳細についてはスペースの関係でここでは触れませんが、別途資料等で調べて下さい。
- ⇒ ディジタル信号処理(基礎編)に戻る

