窓関数 (Window Function)
井澤 裕司
1. 離散フーリエ変換と窓関数
- この章では、
離散フーリエ変換に用いる窓関数
について学習します。
- 長い信号のスペクトル解析では、信号の一部を切り出してフーリエ変換を行います。
- しかも、計算機を用いる場合は、離散値のデータを用いざるを得ず、離散フーリエ変換となります。
- その場合の第1の課題は、切り出すデータの数をどのように決めるかということです。
- データ数が少ないと、周波数分解能すなわちスペクトルの精度が低下してしまいます。
- 一方、データ数が多いと、計算量はデータ数の2乗で増え、処理時間が急激に増えてしまいます。
- 第2の課題は、切り出したデータの両端の影響をどのように押さえるかということです。
- すなわち、離散フーリエ変換では、暗黙のうちにデータの周期性が仮定されているため、
- 右端と左端のデータ値が大きく異なると、その部分で急峻に変化しているような影響が現れ、
- 結果として高い周波数成分(高調波成分)の歪が発生します。
- この対策として、信号に窓関数をかけた結果を離散フーリエ変換します。
- 以下、この窓関数(Window
Function)について解説します。
2. 窓関数(Window Function)の条件
- 入力となる離散信号に窓関数をかけた結果を離散フーリエ変換します。
- この窓関数に要求される条件は、以下の通りです。
- (1)
主成分(メインローブ;main-lobe)の幅が小さいこと
- この幅が狭いほど、主成分の周波数分解能が高くなります。
- (2) サイドローブ(side-lobe)の振幅が小さいこと
- この値が小さいほど、小電力のスペクトルを検出する能力が高まります。
-
3. 窓関数の種類とその効果
- ここでは、代表的な窓関数を紹介し、その効果について解説します。
- (1) 方形窓(Rectangular
Window)
- 入力信号を、単純に切り出してそのまま使用します。
- 主成分の周波数分解能は優れていますが、サイドローブが大きいため、小さい電力のスペクトル
- を検出するのに向いていません。
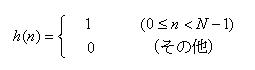
- (2) ハニング窓(Hanning Window)
- この窓関数は中央値が1のRaised Cosineの波形になっています。
- 主成分の周波数分解能はやや劣りますが、サイドローブが比較的小さいため、小さい電力のスペクトル
- を検出するのに向いています。
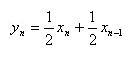
- (3) ハミング窓(Hamming Window)
- この窓関数は窓の両端の値が0となり、実質的にその信号成分がスペクトルに反映されないという
- Hanning Window の欠点に修正を加えたものです。
- 特性はHanning Window に近く、主成分の周波数分解能はやや劣りますが、小さい電力のスペクトル
- を検出するのに向いています。
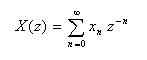
- (4) ガウス窓(Gaussian Window)
- この窓関数は中央が1の釣鐘型をしています。整数mとして±mσ(σ:標準偏差)の範囲
- を対象とします。
- 主成分の周波数分解能は劣りますが、小さい電力のスペクトルを検出するのに優れた特性を示します。
- 下の図は、正弦波入力に窓関数をかけたときのスペクトルを表しています。
- 上が入力波形、中央が窓関数とこれを入力にかけた波形、下がそのスペクトル(絶対値)です。
- 窓関数を選択して、そのスペクトルがどのように変化するか観察して下さい。
ここで、窓関数の効果について検討しましょう。
- 離散信号
xn
に窓関数
hn
を掛けた信号のスペクトル
Xk*
を計算します。
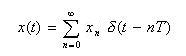
- すなわち、スペクトル
Xk
と
Hk
の畳み込みの形になっており、スペクトル
Xk
をフィルタ
Hk
で平滑化したものと
- 考えることができます。
4. まとめ
- 離散フーリエ変換に使用する窓関数(Window Function)と
その効果について検討しました。
-
⇒ ディジタル信号処理(基礎編)に戻る