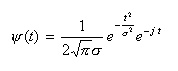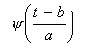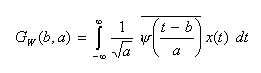短時間フーリエ変換と連続ウェーブレット変換
井澤 裕司
1. はじめに
- 時間により変化する信号
x(t)
をフーリエ変換すると、そのスペクトル
X(ω)
が得られます。
- このスペクトルは、周波数の関数であり、もはや時間の情報は失われています。
- したがって、スペクトルの時間的変化を求めるためには、信号の一部を窓関数(Window Function)を
- 用いて切り出し、この窓をずらしながら、その区間の信号のスペクトルを次々に解析する必要があります。
- 信号の周波数の時間的変化を解析する手法として、
短時間フーリエ変換 (Short-time Fourier Transform)
と
- 連続ウェーブレット変換 (Continuous WaveletTransform)
があります。
- この連続ウェーブレット変換は、短時間フーリエ変換の問題点を解決するために考案された比較的新しい
- 手法であり、現在も様々な機関で研究が行われています。
- 本章では、これらの方式の違いを中心に解説します。
2. 短時間フーリエ変換(Short-time Fourier Transform)
- 短時間フーリエ変換
では、一定の大きさの窓関数を用いて信号を切り出し、その結果をフーリエ変換して
- スペクトルを計算します。
- 設定した1つの窓に対して1組のスペクトルが得られるので、スペクトルの時間的変化を求めたことになります。
- 入力信号
x(t)
を、時間
b
を中心とした
ガウス窓(Gaussian Window)
を用いて切り出した信号のスペクトル
- X(b,ω)
は次のように表されます。
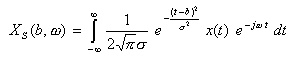
- なお、
σ
はガウス分布の広り、すなわち切り出す信号のサイズを決める定数であり、スペクトルは時間
b
と
- 周波数
ω
の関数となります。
- このようなガウス窓を用いた短時間フーリエ変換を
Gabor変換
と呼ぶことがあります。
-
- ここで、信号に
ガウス窓
を乗じる操作と
フーリエ変換
を1つの変換操作とみなしてまとめると、
- 次のような関数
Gs(t,ω)
が得られます。
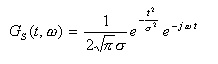
- ここで、
σ
と
ω
は独立であり、例えば
σ
を固定したまま
ω
の値を変化させると、関数
Gs(t,ω)
の形状は
- 複雑に変化します。(極大点と極小点の数は、ほぼ
ω
に比例して増加します。)
- 一般に、周波数の分解能は窓関数のサイズに反比例するので、この窓関数のサイズを大きく設定すると、
- 周波数分解能は向上しますが、時間軸に関する情報、すなわち時間分解能は低下します。
- 一方、窓関数のサイズを小さく設定すると、時間分解能は向上しますが、周波数分解能は逆に低下します。
-
- このように、周波数分解能と時間分解能は、一方が高くなると他方は低下し、これを「不確定性の原理」と
- 言います。
- すなわち、短時間フーリエ変換では、周波数分解能と時間分解能を両立させることができないことを
- 示しています。
- このような問題を解決するため、フランス人の石油探査技師であった
Morlet は、1980年初頭に次に
- 示す連続ウェーブレット変換を考案したと言われています。
3. 連続ウェーブレット変換
(Continuous Wavelet Transform)
- 短時間フーリエ変換では、窓のサイズと周波数を独立に変化させることができます。
- たとえば、上に示したGabor変換では、
σ
を固定したまま
ω
の値を変化させると、関数
Gs(t,ω)
の
- 形状は、複雑に変化します。
- ウェーブレット
とは
「さざ波」
のことですが、このウェーブレット変換では、1つの
マザーウェーブレット
という
- 基本的な関数を
拡大・縮小
させることにより、信号の周波数-時間軸の解析を行う手法です。
- 上記Gabor変換に対応するマザーウェーブレットを、次式で表します。
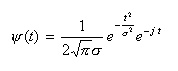
- この関数
ψ(t)
は、複素正弦波にガウス関数を乗じたものとなっていますが、周波数
ω
に依存しない
- ことに注意して下さい。
- ここで、上のマザーウェーブレットを基にして、時間方向に拡大・縮小・シフトした次の関数を用います。
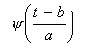
- パラメータの
a
は、マザーウェーブレット
ψ(t)
を時間方向に拡大・縮小する比率を決定するものであり、
- 周波数に相当します。
- また、パラメータの
b
は、短時間フーリエ変換と同様時間のシフト量に対応し、ガウス窓の位置(解析する時間)
- を決定します。
- この関数を用いて、連続ウェーブレット変換を次のように定義します。
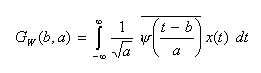
- ここで示した連続ウェーブレット変換を、Gaborのウェーブレット変換(時に、単にGabor変換)と言います。
- 短時間フーリエ変換であるGabor変換と混同しないよう注意が必要です。
- なおこの変換は、フーリエ変換で成立したような直交基底の条件を満たしません。
- 短時間フーリエ変換
と
連続ウェーブレット変換
の違いについて、次の図を用いて具体的に説明しましょう。
-
- 左は
短時間フーリエ変換
の基底関数
Gs(t,ω)
、右は
連続ウェーブレット変換
の基底
ψ{(t-b)/a}
を表しています。
- この表示では、周波数の変化に伴い、
短時間フーリエ変換
の基底関数の形状が変化するのに対し、
- 連続ウェーブレット変換
の基底関数はすべて相似形であり、1つのマザーウェーブレットを拡大・縮小したものが
- 使われていることがわかります。
- 連続ウェーブレット変換
では、周波数が高くなるについて、そのサイズも小さくなり、時間軸の詳細な情報を
- 検出できます。
- その例を次に示しましょう。
- (1) 短時間フーリエ変換(Gabor 変換)
- はじめに、短時間フーリエ変換
(Gabor 変換)を用いた解析例を示します。
- 上が、解析に用いた入力信号であり、途中の数カ所で不連続な箇所が含まれています。
- 中央がスペクトルの振幅成分であり、明るいほど振幅が大きくなっています。
- 下はスペクトルの位相成分であり、それらの位相を色を用いて表現しています。
- (2) 連続ウェーブレット変換 (Gabor)
- 次に、Gaborによる連続ウェーブレット変換による解析例を示します。
- 上が、解析に用いた入力信号であり、途中の数カ所で不連続な箇所が含まれています。
- 中央がスペクトルの振幅成分であり、明るいほど振幅が大きくなっています。
- 下はスペクトルの位相成分であり、それらの位相を色を用いて表現しています。
- (1)の短時間フーリエ変換と比較すると、不連続成分がより明瞭な形で表示されていることが分かります。
4. 代表的な連続ウェーブレット関数
- 連続ウェーブレット変換のマザーウェーブレットとして、以下のような関数が用いられます。
- (1) Gabor
のウェーブレット
- 先に示したように、Gabor
のウェーブレット関数は複素数となり、以下のように表されます。
- 時間 t
の絶対値が大きくなっても、この関数値は完全に0にはならず、いわゆる「コンパクト・サポート」
- ではありません。
- 先に触れたように、直交ウェーブレットではありませんが、信号の局所的な周波数成分を検出するのに
- 用いられます。
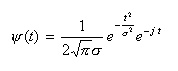
- (2) Mexican hat
- ガウス関数の2次の導関数はメキシカンハットのような形状となり、これをマザーウェーブレットとします。
- 式で表すと次のような実関数となりますが、これも直交ウェーブレットではありません。
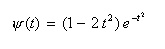
- (3) French hat
- この関数も次式で示されるような実数値であり、(2)のMexican
hat を矩形を用いて単純化したような
- 形状をしています。
- 両端で完全に0となるので、コンパクト・サポートと呼ばれますが、直交ウェーブレットではありません。
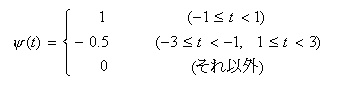
- (4) Meyerのウェーブレット
- Meyerは、フーリエ変換を用いた直交ウェーブレットの構成法を示しました。
- まず、スペクトル領域で中央が1、両端が0となり、その間が滑らかに接続する次のような関数
XM(ω)
を求めます。
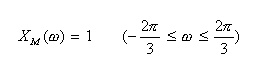
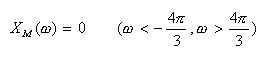
- 1と0の間を、下に示す角速度 ω の多項式
g(ω)
を用いて接続します。ここで n は整数です。
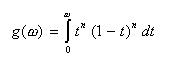
- 例えば n=3 のとき、
g(ω)
は次のようになります。
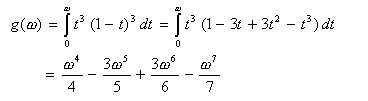
- この
g(ω)
を用いて、関数
XM(ω)
を下の式のように定義すると、滑らかに接続するスペクトルが得られます。
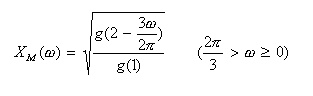
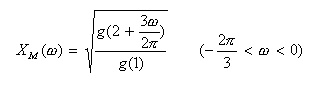
- 関数
XM(ω)
を逆フーリエ変換したのが、次のスケーリング関数φ(t) です。
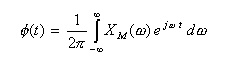
- このスケーリング関数φ(t) を用いて、次のようにウェーブレット関数ψ(t) を求めることができます。
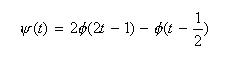
- この Meyerのウェーブレット関数は実数の直交ウェーブレットですが、いわゆるコンパクト・サポートではありません。
- 下の図に、これらのマザーウェーブレットの形状を示します。
- これらの関数以外にも、様々な連続ウェーブレット変換が用いられています。
- それぞれ一長一短があり、解析する信号の内容により、使い分けられています。
[補足] - Meyerのウェーブレット -
- 下の図を用いて、Meyerのウェーブレットについて補足説明します。
- 図の上は n=3におけるスペクトル
XM(ω)
の形状であり、1と0の間が滑らかに接続されていることがわかります。
- 中央に、このスペクトルを逆フーリエ変換して求めた
スケーリング関数 φ(t)
を示します。
- 下は、スケーリング関数から求めた
ウェーブレット関数 ψ(t)
です。
- なお、これらの関数は、無限回微分可能です。
4. まとめ
- 短時間フーリエ変換と連続ウェーブレット変換についてその違いを中心に解説し、代表的な連続ウェーブレットをいくつか
- 紹介しました。
- この連続ウェーブレット変換に対応するものとして、離散ウェーブレット変換があります。
- その中で特に重要なDaubechiesによる離散ウェーブレット変換については、応用編で解説いたします。
-
⇒ ディジタル信号処理(応用編)に戻る