離散コサイン変換 （Discrete Cosine Transform ; DCT）

本章では、画像を圧縮するJPEGやMPEG等の符号化方式に用いられている 離散コサイン変換

(Discrete Cosine Transform) について、解説します。

後ほど解説しますが、この離散コサイン変換は本資料の基礎編で解説した離散フーリエ変換の

特殊な場合と考えられ、実数の信号を同数の実数の変換係数に変換します。

離散フーリエ変換に比べ、特定の周波数成分に電力が集中しやすく、符号化効率が高いため、

画像符号化の標準化方式にも採用されています。

図１に、JPEG方式による静止画像の符号化手順を示します。

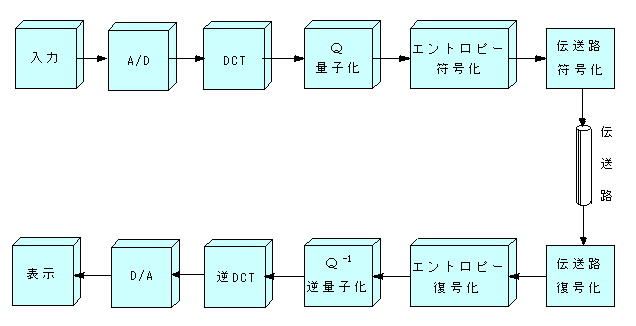
　　　　　　　　　　　　　　　　　　　　　図１　JPEG方式による画像の符号化

Ａ／Ｄ変換された画像信号は、縦横 (8×8) 画素のブロックに分割され、以降の処理は、このブロック単位に行ないます。

画像信号は離散コサイン変換(DCT)により、同数の変換係数に変換され、量子化されます。

この量子化の出力はエントロピー符号化され、伝送路符号化の後、伝送路に送出されます。

一方の受信側では、これと逆の処理が行われます。

なお、原画、変換係数、復号画像は、いずれも同形（8×8）のマトリクスで表すことができます。

以下、量子化とエントロピー符号化について補足しましょう。

量子化は下の図に示すように、DCTの変換係数を近似する操作です。

このステップの幅をステップサイズと言い、このステップサイズが均一であるとき、線形量子化と呼びます。

　　　　　　　　　　　　　　　　　　　　　　図２　量子化

ステップサイズを適応的に切り替えることにより、符号化後のビット数と画質を制御することができます。

なお、図のハッチング部が量子化誤差に相当し、これが歪の原因となります。

量子化した変換係数は図３に示すように、低い周波数成分（直流）から高い周波数成分へとジグザグ状にスキャンされます。

またブロック間については、左上のブロックから右下のブロックへと順次伝送されます。

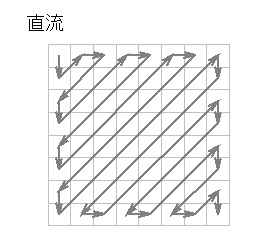
　　　　　　　　　　　　　図３　量子化した変換係数のジグザグスキャン

一般的な画像の場合、ＤＣＴの変換係数の絶対値は、高い次数の周波数成分ほど小さな値になる傾向があります。

したがって、量子化出力では、ある係数からブロックの最高次の係数まで０が連続する確率が高くなります。

この場合には符号化効率を向上させるため、ブロックの終りを示す短い符号（ＥＯＢ：End Of Block ） を送出します。

これらの係数はエントロピー符号化されて、伝送路に送出されます。

エントロピー符号化とは、図４に示すように、出現頻度の高いシンボル（量子化された変換係数）に短い符号、

逆に出現頻度の低いシンボルに長い符号を割り当てる手法であり、代表的なものにハフマン符号化や、

算術符号化があります。

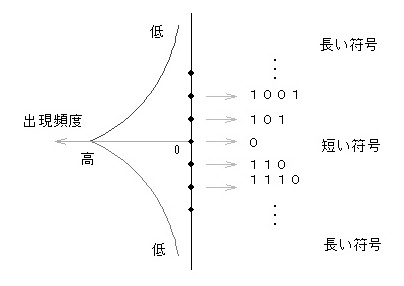
　　　　　　　　　　　　　　　　　　図４　ハフマン符号

なおこれらの詳細については、文献等で調べて下さい。

それでは、離散コサイン変換について説明しましょう。

離散コサイン変換 の定義は以下のようになります。

入力信号を x_i　( i = 0,1,2,‥,n-1) 、変換した係数を c_i　( i = 0,1,2,‥,n-1) とします。

これらをベクトル x^, c^ を用いて表わすと、変換と逆変換は以下のように定義されます。

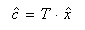
(変換）

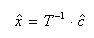
(逆変換）

ここで、マトリクス T は (n×n) となり、 i 行 j 列の項は以下の式で与えられます。

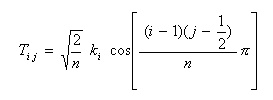
ここで変換行列 T は正則で、逆行列　T^-1が存在します。

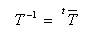
なお、 t は転置行列、 バー は複素共役を表しています。このような行列を ユニタリ行列 と呼び、

このような行列で表される変換を ユニタリ変換 と言います。

なお、 離散コサイン変換（DCT） のように、T の各項がすべて実数で構成される場合、次のようになります。

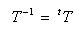
また、係数 ki ( i = 0,1,2,‥,n-1) は以下のようになります。

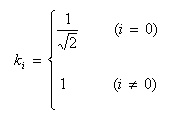
i = 0 のとき直流、他の場合はコサインの波形となります。

ki は、それらの実効値を一致させるための係数です。

これらの関係を直観的に示すため、(8×8)の場合について、省略しない形式に書き直してみましょう。

変換側は以下のようになります。

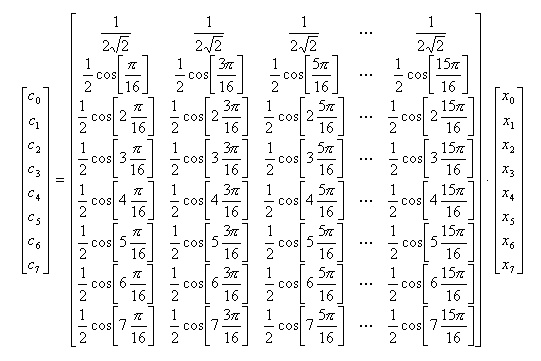
また、逆変換は以下のようになります。

この離散コサイン変換の物理的な意味を、下の図を用いて説明してみましょう。

8個の実数で表される信号 xi ( i = 0,1,2,‥,7) は、下図のようなコサインの重ね合せで表すことが可能です。

8個の変換係数 cj ( j = 0,1,2,‥, 7) は、それぞれのコサインの成分の大きさに対応します。

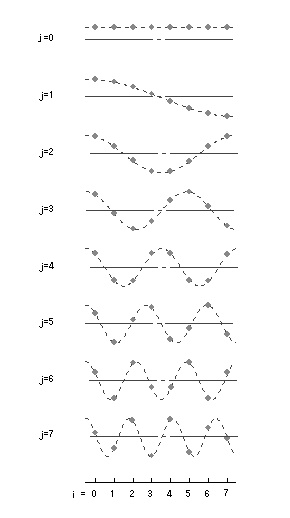
　　　　　　　　　　　　図５　離散コサイン変換（DCT）の解釈

上記コサインの関数 tj で表すと、逆変換の式は次のようになります。

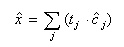
一般的な画像信号では、隣接する画素間に強い相関があり、比較的低い周波数成分に電力が集中する傾向

があります。

このため、低い周波数のコサイン成分の絶対値が大きく、高い周波数成分の絶対値が小さくなり、

エントロピー符号化により大幅に情報量を圧縮することができます。

次に、離散コサイン変換と離散フーリエ変換の関係について、解説しましょう。

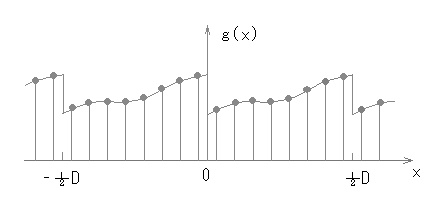
離散フーリエ変換では、下の図に示すように、暗黙のうちに周期的な離散信号を扱っています。

このため、各周期の境界部分で生じる段差成分が、高い周波数成分を発生させる原因となり、

特定の成分への集中度を低める結果をもたらします。

一方の離散コサイン変換では、下の図に示すように、鏡像を用いて任意の信号から周期が倍の偶関数を生成し、

これを離散フーリエ変換した結果に等価です。

偶関数化のため、離散フーリエ変換の係数は全て実数となり、その実係数も偶関数となるため、

実質的に離散信号と同数の変換係数が得られます。

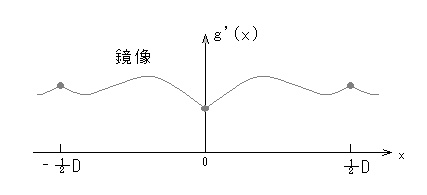
すなわち、離散コサイン変換は暗黙のうちに周期が2倍の偶関数を対象としており、各周期の接続部で滑らかに

接続するため、特定の変換係数への集中度が離散フーリエ変換より改善されます。

これらの関係を、次の図を操作して確認して下さい。

画像信号を圧縮するため、１次元の離散コサイン変換を2次元に拡張します。

1次元で用いた変換マトリクス T を用い、変換は次のように表されます。

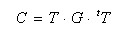
また、逆変換は次のようになります。

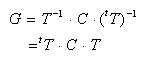
これらを簡単に説明すると、次のようになります。

離散コサイン変換は、任意の画像信号を、以下に示す2次元の基底関数の重ね合わせで表します。

この成分の大きさが各係数に対応しており、低い周波数成分に電力が集中している一般的な画像では、

左上の係数の周辺の値が大きくなり、右下になるほどその絶対値は小さくなります。

すなわち、任意の画像信号は、下の図に示す 2次元離散コサイン変換 の基底関数の重ね合わせにより、

表すことができます。

参考までに、2次元離散サイン変換に基底も表示できます。また、2次元の 離散コサイン変換 と離散サイン変換の

基底の 差 をとると、2次元フーリエ変換の基底（実数部）になります。

なぜ、和ではなく差となるのか、各自考えて見て下さい。

このような重ね合わせの関係を式で表すと、次のようになります。

なお、δij はクロネッカーの関数です。（i = j のとき1、それ以外は 0 ）

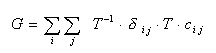
［確かめてみよう］　　−　2次元離散コサイン変換　−

実際に2次元信号を、離散コサイン変換してみましょう。

下の図に、信号と係数の関係を示します。

　

特に、信号が比較的に滑らかに変化している場合、低域係数へ電力が集中することに注意して下さい。

　

5．　まとめ

離散コサイン変換について解説し、離散フーリエ変換との違いについて整理しました。

なお、JPEGやMPEG方式の詳細については、別途解説する予定です。