井澤 裕司
近年、画像信号の圧縮や解析の有力な手法としてウェーブレット変換が注目されている。従来のフーリエ変換が、三角関数を基底とした直交変換であるのに対し、ウェーブレット変換では、局所化された関数から作られる相似関数系を基底とする。これにより、周波数精度は若干低下するが、時間−周波数の同時分解が可能となる。[1]
ウェーブレット変換には、連続ウェーブレット変換と離散ウェーブレット変換がある。前者は、データのパターンや相似性の解析に用いられるのに対し、後者は収束性のよい正規直交系となるため、データ圧縮やエネルギ解析等に用いられる。[2]
ここでは、画像圧縮への応用が期待されている離散ウェーブレット変換(以下、単にウェーブレット変換という)について解説する。なお、ウェーブレット変換は、サブバンド符号化(帯域分割/合成フィルタ)との関連が深い。その内容については、文献[14]-[20]を参照されたい。
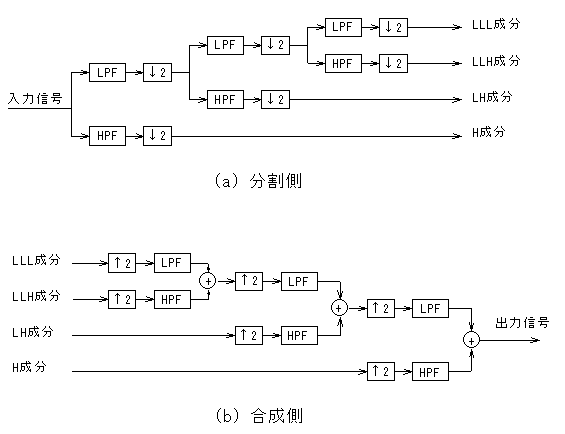
ウェーブレット変換は、一種のサブバンド符号化であり、低域側について分割/合成の処理をツリー状に繰り返すオクターブ分割により表すことができる。図1に3段構成の例を示す。これらは、ローパスフィルタ(LPF)、1サンプルおきに信号を間引くサブサンプラ、各サンプルの間に値 0 を挿入するアップサンプラ、加算器により構成される。図の3段構成の場合、H、LH、LLH、LLLの4帯域への分割となる。

図1 ウェーブレット変換の構成法
このフィルタを従属接続することにより、2次元以上に拡張することもできる。図2に1次元と2次元のオクターブ分割の例を示す。
(1) 1次元信号
3段構成の場合、図2(a)に示すような4帯域(LLL、LLH、LH、H)に分割される。
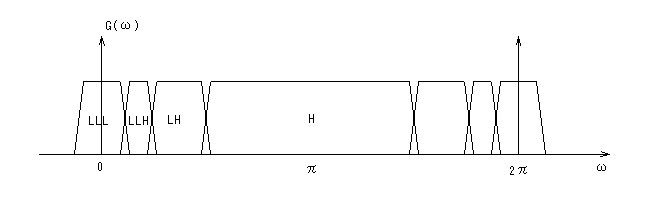
図2(a) 1次元におけるオクターブ分割
(2) 2次元信号
水平2段、垂直2段の構成の場合、図2(b)に示すような7つの帯域に分割される。
(ここで、LLLL成分は、画像縦横サイズを1/4に圧縮した縮小画像、LL成分(=LLLL+LLLH+LLHL+LLHH)は、1/2の縮小画像に対応する。)
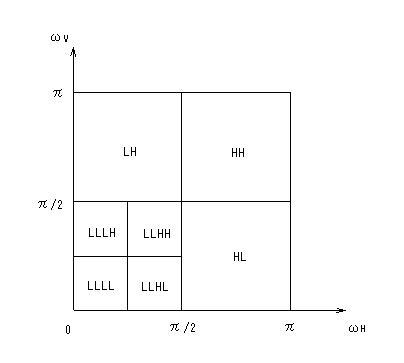
図2(b) 2次元におけるオクターブ分割
ウェーブレット変換は、一種のサブバンド符号化であり、次のような特徴がある。[21]
ウェーブレット変換では、一般的なサブバンド符号化の分割法と異なり、高域側の分割を繰り返さない。このため、高域成分に対応する基底の長さ(≒フィルタのタップ数)が短くなり、動画像におけるモスキート雑音(ブロック境界で蚊が飛んでいるように見える)が目立ちにくいという長所がある。
このように、ウェーブレット変換(サブバンド符号化)にはスケーラビリティとコンパチビリティ等、従来方式にはない特長を有していることから、JPEG2000等の方式に採用されている。
本節では、主として画像圧縮への応用を目的とした離散ウェーブレット変換の構成法について述べる。
はじめに、ウェーブレット変換の性質について述べる。次に、最も基本的なウェーブレット変換と考えられる Haar の基底を紹介し、これを一般化した Daubechies の基底について解説する。
φ(x)をスケーリング関数、ψ(x)をそのウェーブレット変換とする。
このとき、kを整数として、次の関係を満たす数列 {αk}、{βk}が重要な役割を果たす。
(後述のディジタルフィルタにおけるタップ係数に等価となる。)
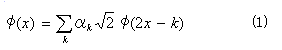
![]()
![]()
ここで
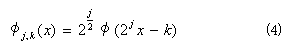
![]()
とすると、φを選択することにより、
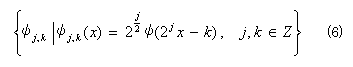
を完全正規直交系とすることができる。すなわち、任意の2乗可積分関数 f(x)∈L2(R)について、次式が成立する。
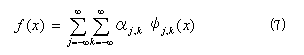
![]()
ここで、バーは複素共役、添字 j は2倍ごとの拡大・縮小を表すパラメータである。したがって、式(8)は、2倍ずつ解像度を上げながら、関数 f(x) を観察する過程に対応する。この概念を抽象化したものが、いわゆる「多重解像度解析」[6]である。
このとき、次の関係がある。
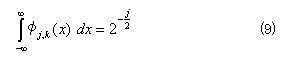

ここで、Vn をφn,k で張られるL2の線形部分空間、Wn をψn,k によって張られる部分空間であるとすると、次式が成立する。
![]()
なお、Wnは VnのVn+1における直交補空間である。
以下、これらの関係について、Haar および Daubechies の基底を用いて具体的に説明する。
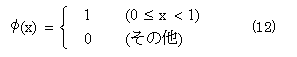
このとき、次の関係が成立する。
![]()
![]()
すなわち、式(1)-(3)において、次のようにおいたものに等しい。
![]()
![]()
![]()
![]()
図3に、Haarによるスケーリング関数φとウェーブレット関数ψ、図4にその基底の例を示す。
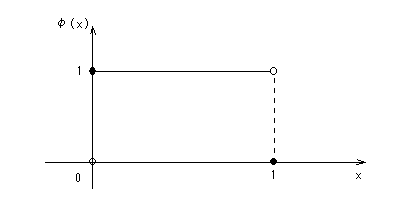
図3(a) Haarによるスケーリング関数φ
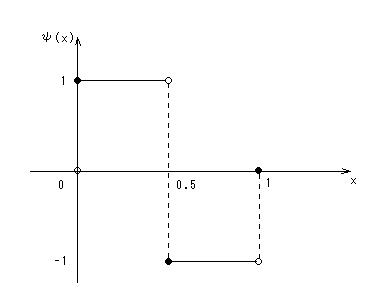
図3(b) Haarによるウェーブレット関数ψ

図4 Haarの基底の例
図4より、φj,k について、以下の関係が成立することは明らかである。
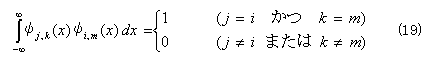
すなわち、ウェーブレット関数から作られる基底ψj,kは完全正規直交系となる。また、φj,k(x)およびψj,k(x)とx軸で囲まれる4角形の面積を計算すれば、式(9)(10)が成立することも明らかである。
このように、Haarの基底を用いることにより、任意の2乗可積分関数 f(x)を、周波数と場所(時間)の成分αj、kにより表現することが可能となる。ここで、添字の j は周波数、k は場所(時間)に対応するパラメータである。
しかしながら、この基底が不連続となるため、一般的な自然画像の圧縮には適さない。この不連続を解消すると同時に、Haarの基底の一般化に成功したのが、次に示すDaubechiesによるウェーブレット関数(基底)である。
Daubechiesはコンパクトサポートなウェーブレット関数を構成し、式(1)-(3)を満たす数列{αk}を求めた。表1にその一部を示す[6][7]。なお、N=1(2タップ)の場合は、前節のHaar基底に一致する。
表1 Daubechiesの数列 {αk}
| N | k | αkの値 |
| 1 | 0 1 |
0.707106781 0.707106781 |
| 2 | 0 1 2 3 |
0.482962913145 0.836516303738 0.224143868042 -0.129409522551 |
| 3 | 0 1 2 3 4 5 |
0.332670552950 0.806891509311 0.459877502118 -0.135011020010 -0.085441273882 0.035226291882 |
| 4 | 0 1 2 3 4 5 6 7 |
0.230377813309 0.714846570553 0.630880767930 -0.027983769417 -0.187034811719 0.030841381836 0.032883011667 -0.010597401785 |
図5に N=2, 3, 5 におけるスケーリング関数φ(x)とウェーブレット関数ψ(x)の例を示す。
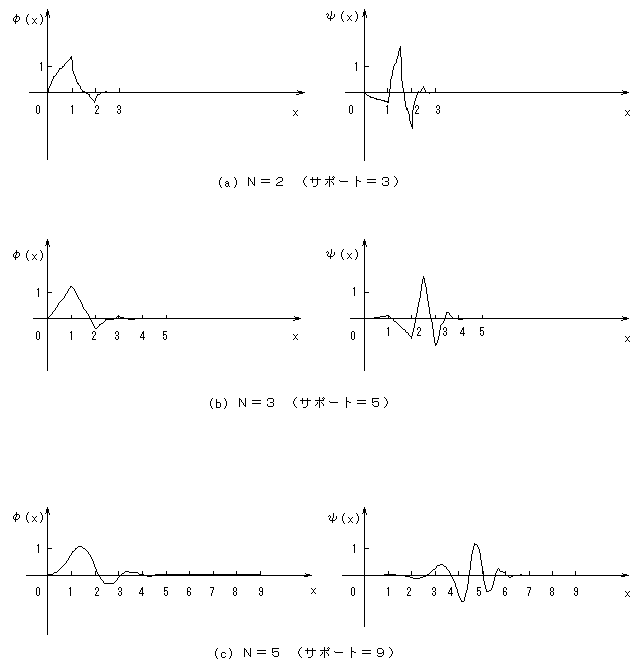
図5 Daubechiesによるスケーリング関数φ(x)とウェーブレット関数ψ(x)
ここで、最も簡単なN=2におけるスケーリング関数φ(x)の性質について補足する。表1の数列{αk} (k=0,1,2,3) を用いると、式(1)は次のようになる。
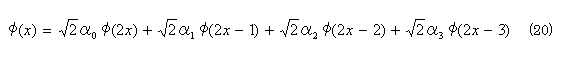
すなわちφ(x)は、それ自身を1/2に縮小し、かつ1/2ずつシフトした4つの関数の重ね合せにより表現することができる。この関係を図6に示す。
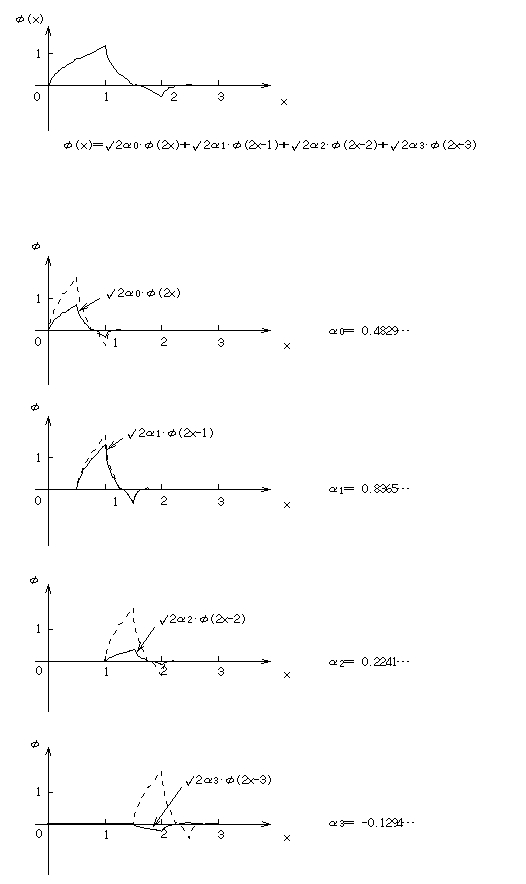
図6 Daubechies(N=2)におけるスケーリング関数φ(x)の性質
さらに、図7にこの関数で構成される直交関数系の基底の一部を示す。
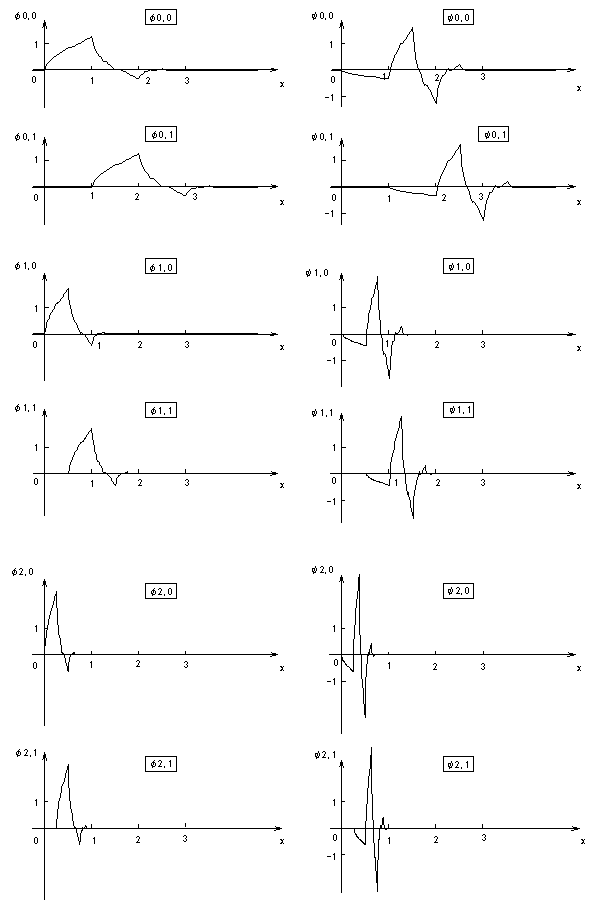
図7 Daubechies(N=2)の基底の例
Daubechies によるコンパクト・サポートをもつウェーブレット関数ψに関連して、以下の定理が証明されている。[6]
[定理1]
すべての整数 Nに対して、以下の4条件を満たす数列{αk;k∈Z}が存在する。ここで、δ0mはクロネッカーのデルタ関数である。
![]()
![]()
![]()
![]()
ここで、βk=(-1)kα1-k (=式(2))である。
[定理2]
N ≧ 2, {αk}について式(1) を満たし、コンパクト・サポートで
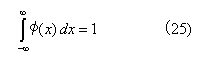
を満たす解φ(x)がただ1つ存在する。このスケーリング関数φのサポートは[0, 2N-1]である。さらに、式(3) を満たすウェーブレット関数ψもコンパクト・サポートであり、次の条件を満たす。
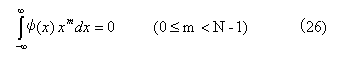
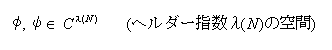
ここで、
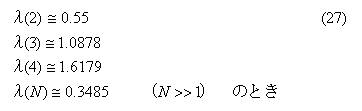
以下、4タップ(N=2)および6タップ(N=3)の場合について、これらの係数を求める。
フィルタのタップ係数を α0, α1, α2, α3とする。このとき、式(22)より、次の2条件が導かれる。
![]()
![]()
さらに、式(23)より
![]()
一方、式(24)より、 m = 0,1 として、
![]()
このとき、式(2)より
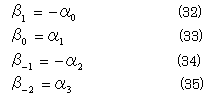
これらを式(31)に代入すると、m=0,1 として
![]()
すなわち
![]()
![]()
式(29)(29)(30)(37)(38)より、α0, α1, α2, α3を求めると次のようになる。
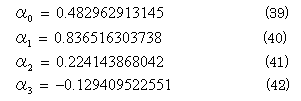
6タップ(N=3 ; D6)の場合
式(22)より、次の3条件が定まる。
![]()
![]()
![]()
さらに、式(23)より
![]()
このとき、式(2)より
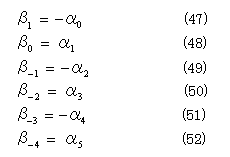
一方、式(24)より、 m = 0,1,2 として、
![]()
上式に式(47)-(52)を代入すると、m = 0,1,2 として
![]()
すなわち、
![]()
![]()
![]()
式(43)(44)(45)(46)(55)(56)(57)より、α0, α1,…,α5を求めると次のようになる。

4.4 スケーリング関数およびウェーブレット関数の離散化
画像符号化では、画像信号をサンプリングされた離散値として処理する。このため本節では、これまで述べてきたスケーリング関数およびウェーブレット関数の離散化について検討し、離散ウェーブレット変換の具体的構成法を明らかにする。なお、簡単化のため1次元で説明するが、2次元以上への拡張は容易である。
4.4.1 データ補間法
はじめに、サンプリングされた離散値から、サンプリング周波数を2倍にアップレートした場合の補間値を求める手法について解説する。この手法は、以下に示す(1)〜(4)の手順により構成される。
(1) 連続関数 g(t)のサンプリング
いま図8に示すように、連続関数 g(t)を一定の周期Tのサンプラを用いてサンプリングする。このとき、サンプリング周波数は fs(=1/T)であり、入力信号は g(nT) (n=…,-1,0,1,…) で表される。
ここで g(nT)のz変換を g(z)とすると、次式が成立する。
![]()
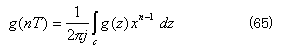
式(65)の C は、 g(z)の極を内部に含む閉路積分を表す。なお、z-1 はサンプリング周期Tに対応する単位遅延要素と考えることができる。
(2) アップサンプリング(0挿入)
サンプリングされた入力信号 g(nT)から、2倍のサンプリング周波数 fs'=2fs(周期;T'=T/2)における値を求めるため、図9(b) に示すように、各周期の中央に新たなサンプリング点を設け、値 0 を挿入する。この処理をアップサンプリングという。
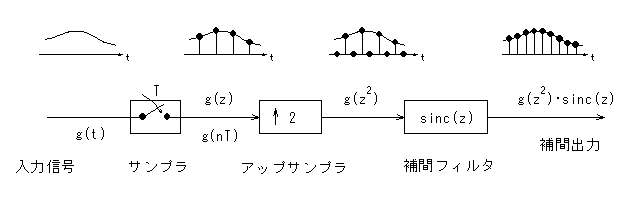
図8 データ補間法
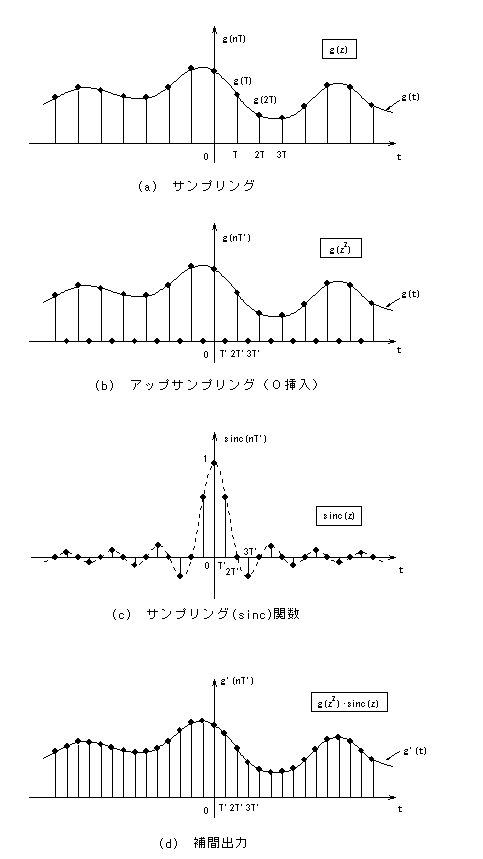
図9 データ補間法
アップサンプリングの処理は、式(64)のzをz2に置き換える操作に等しい。すなわち、
![]()
として、次式が成立する。
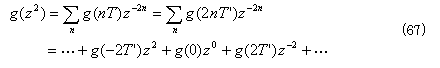
ここで、zの奇数次(例えば、z-1,z1,z3,…)の項はない。すなわち、k を整数として
![]()
を想定しており、奇数項に0を挿入したことに等価となる。
(3) 補間フィルタ
代表的な補間フィルタとして、図10に示すような理想的周波数特性をもつローパスフィルタがある。(ハーフバンド・フィルタという。)
このフィルタのインパルス応答は、以下に示すサンプリング関数(sinc 関数)となる。
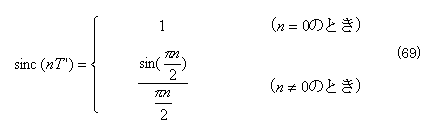
![]()
この関数の形状を図9(c)に示す。図から明らかなように、その定義域は−∞〜+∞となる。
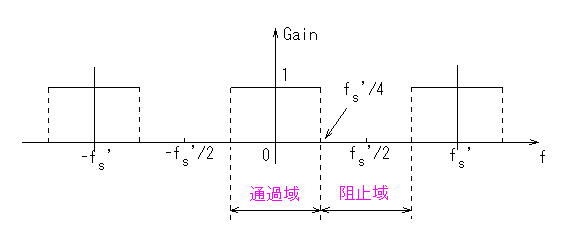
図10 補間フィルタの周波数特性
(4) 補間処理
アップサンプリング(0挿入)の出力 g(z2)を、前項の補間フィルタに入力すれば、補間出力 g'(z)が得られる。補間フィルタの伝達関数(z変換)として式(70)を用いると、アップサンプリングと補間の処理は、次式のようになる。
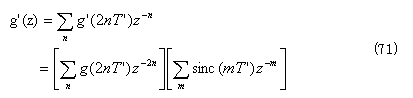
ここで、式(69)のサンプリング関数において、次式が成立する。(ただしk;整数)
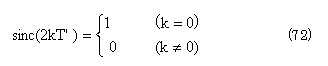
したがって、図9(d)の偶数番目の補間出力(…,g'(-2T'),g'(0),g'(2T),…)は、同図(a)の原信号 g(x)のサンプル値(…,g(-T),g(0),g(T),…)に等しくなる。
なお、すべての補間出力 g'(nT')が原信号 g(t)上に存在するためには、関数 g(t)がナイキストの条件(fs/2以上の周波数成分を含まない)を満たす必要がある。
4.4.2 スケーリング関数とウェーブレット関数の離散的表現
本項では、スケーリング関数とウェーブレット関数の離散的表現について検討する。
いま、式(1)(3)の変数 x を、サンプリング周期Tのクロックを用いて離散化する。なお、i を正の整数として、周期Tを次のように設定する。(この根拠は次項で説明する)

このとき、式(1)よりスケーリング関数φ(nT)のz変換は、次のようになる。
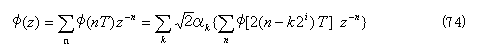
同様に、ウェーブレット関数ψ(nT)のz変換は、式(3)より、
![]()
となる。
ここで、式(74)(75)の第2項の関数 φ[2(n-k・2i)T] において[]内が0となるのは、
![]()
となる場合である。すなわち、関数 φ[2(n-k・2i)T] は φ(2nT) を正の方向に k・2i クロック分シフトさせたものに等しい。
したがって、
![]()
が成立し、式(74)(75)は、以下のように書き換えられる。
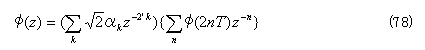
![]()
さらに、式(1) より、
![]()
が成立し、関数 φ[4(n-k・2i-1)T] は φ(4nT) を正の方向に k・2i-1クロック分シフトさせたものに等しいから、式(78)(79)は、
![]()
![]()
となる。同様にして、φ(z)およびψ(z)を次のように書き直すことができる。
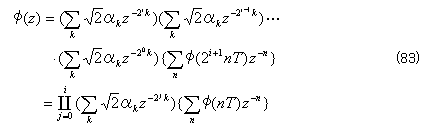
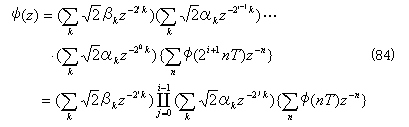
これらの式において()で示される項は、ひとつのディジタルフィルタと考えられる。したがって、スケーリング関数とウェーブレット関数は、これらのディジタルフィルタを従属(カスコード)に多段接続したものとして表現できることがわかる。次項では、その具体的な構成法について述べる。
4.4.3 補間フィルタのカスコード接続
前節で述べたように、サンプリング関数(sinc 関数)の定義域は−∞〜+∞ となり、∞タップのフィルタが必要となる。そこで、サンプリング関数のかわりに、定義域が比較的狭い(コンパクト・サポート)関数 r(x) を定義し、そのz変換を r(z)とおく。
![]()
ここで、rn = r(nT) である。図11(a)に4タップの例を示す。
(なお、係数 rn は表1で示した Daubechies のN=2におけるタップ係数に√2を掛けたものに等しく、 n = 0,1,2,3 である値をもち、それ以外で0となる。)
次に、このフィルタを補間フィルタとみなし、アップサンプリングと補間処理をカスコード(縦属)に多段接続した場合のフィルタ特性について検討する。
(1) 1段目アップサンプリング(0挿入)
サンプリング周波数が2倍のアップサンプリングは、式(85)のzをz2で置き換えればよい。すなわち、図11(b) に示すように、その出力は r(z2)となる。
(2) 1段目補間出力
1段目アップサンプリング(0挿入)の出力 r(z2)を、2段目の補間フィルタ r(z)に入力すると、その出力は r(z2)・r(z) となる。(図11(c) 参照) このとき、サンプル数 n に関する定義域(非ゼロとなる係数の幅)を N1 とすると、次の関係式が成り立つ。
![]()
ここで、N0 は rn のタップ数(図11では 4 )である。上式右辺の 2・N0 - 1 はアップサンプリング、 N0 - 1 は補間フィルタの処理に対応する。
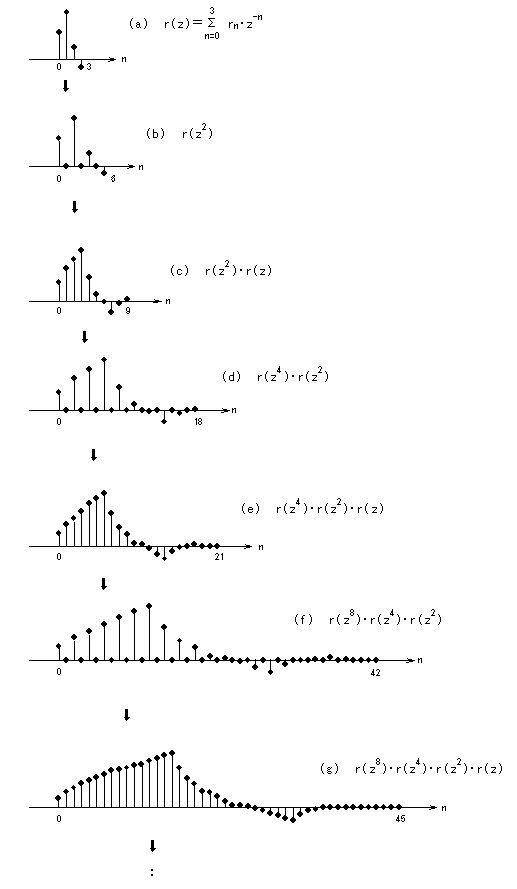
図11 補間フィルタのカスコード接続
(サンプル数 n に関する定義域の変化)
(3) 2段目アップサンプリング(0挿入)
図11(d) に示すように、この操作は r(z4)・r(z2)で表される。
(4) 2段目補間出力
同図(e) のように、その出力は r(z4)・r(z2)・r(z) となる。このとき、サンプル数 n に関する定義域を N2 とすると、次の関係が成立する。
![]()
図11(f),(g)に示すように、3段目についてもアップサンプリングと補間処理の出力は、それぞれ r(z8)・r(z4)・r(z2)、 r(z8)・r(z4)・r(z2)・r(z)となり、サンプル数 n に関する定義域 N3 は、
![]()
となる。これより、i段目の補間出力を hi(z) とおくと、
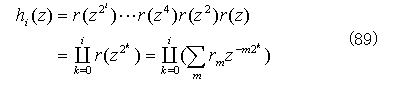
となり、
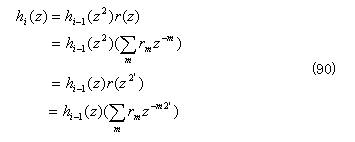
が導かれる。また、i 段目の補間出力のサンプル数 n に関する定義域 Ni は、
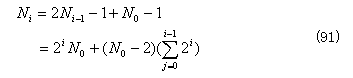
となる。
一方、i 段目の補間出力のサンプリング周期は 2-i・T となる。したがって、時間 t に関する定義域を τi とおくと、
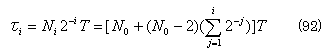
ここで、i → ∞ とすると、
![]()
となり、関数 hi(nT)の定義域(サポート)が、一定値[2(N0 - 1)T]に収束することがわかる。図11と同じ条件における、時間 t に関する定義域の変化を図12に示す。
(なお、図11はサンプル数 n に関する定義域の変化に相当する。)
ここで重要なことは、段数の増加につれ補間出力のエンベロープが一定の形状に収束することである。(ただし、あらゆる rn について収束するという保証はない。)
すなわち、 rn を適切に選んだとき、関数 hi-1(z)および、hi(z)を逆z変換して得られる元の関数をそれぞれ hi-1(nT)、hi(nT) とすると、i を十分大きくとることにより、
![]()
とすることができる。すなわち、
![]()
が成立するとき、式(90)を逆z変換すると、
![]()
が導かれる。ここで、式(73)より、 T = 2-(i+1) とおくと、式(96)は
![]()
となる。これより、
![]()
とすれば、h(t) がスケーリング関数φ(t)そのものであることが示される。
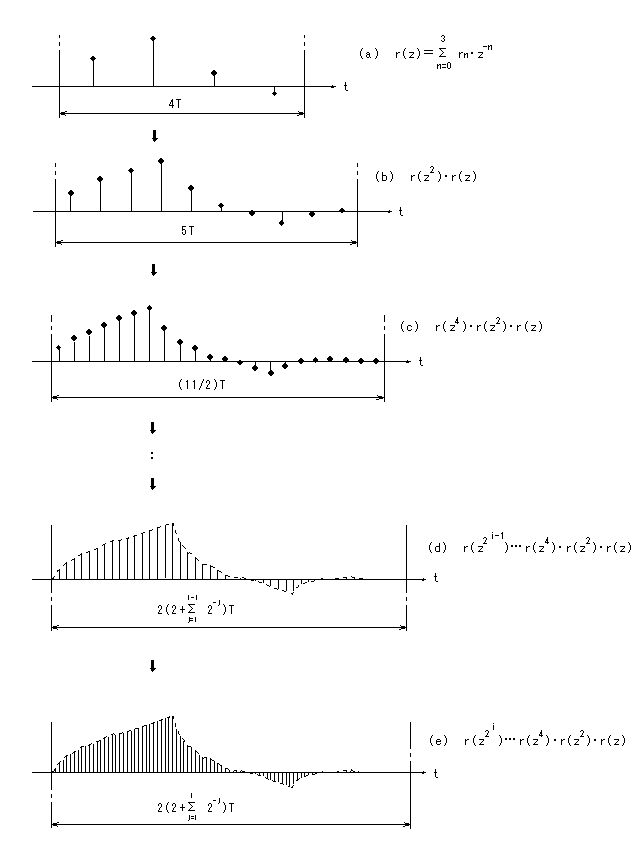
図12 補間フィルタのカスコード接続
(時間 t に関する定義域の変化)
以上、h(nT) がスケーリング関数であることを示したが、これを用いて
![]()
を定義すれば、これがウェーブレット関数となる。
このように、図12に示したスケーリング関数は複雑な形状をしているが、表1に示すパラメータ αk により、完全に記述されることがわかる。一方の、ウェーブレット関数についてもパラメータαk, βk のみを用いて記述できる。
ここで表1のパラメータ αk をタップ係数とするフィルタをローパスフィルタ(LPF)とすれば、 βk をタップ係数にもつフィルタはハイパスフィルタ(HPF)に相当する。
そこで、これらの2種類のフィルタをカスコード接続して、図13(a) に示す補間フィルタを構成する。図のように入力を P0〜P5、各段の出力を Q1,Q2,…,Q5 とする。ここで、入力に単位インパルス δ(t) を加えたときの各段の出力を求めると、図13(b)のようになる。なお、図1(b)で明らかなように、図13(a)の補間フィルタはウェーブレット変換の合成側の構成そのものであることがわかる。
ここで、最も低次の入力 P0(LLLLL成分)については、アップサンプラとLPFを多段接続した構成となる。すなわち、4.4.3 で示したように、出力信号 Qi (i=1,2,3,…)はスケーリング関数に収束する。(この関係は式(91)と、単位インパルス δ(t) のz変換 δ(z) = 1 であることから明らかである。)
一方、次の P1(HLLLL成分)については、ウェーブレット関数に収束する。また、P2(HLLL成分)は、P1を1段分シフトしたものに等価であり、入力とするインパルス(係数)の数は、P0(P1)の2倍必要となる。さらに、P3(HLL成分)は、P2を1段シフトしたものであり、インパルスの数は、P2 の2倍(P0の4倍)となる。
したがって、図13(b) の出力 Q5 のレベルで考えると、32 個のサンプル値で構成される任意の波形は、P0〜P5 の6種類の波形の重ね合わせにより表すことができ、それぞれの成分の大きさがインパルスの高さ(単位インパルスにある係数を掛けたもの)に対応する。ここで、係数の数については、P0(P1)が1、P2,P3,P4,P5 はそれぞれ、2,4,8,16 となり、その総数は、32(1+1+2+4+8+16)となる。すなわち、32個のデータは同数の係数に変換される。ここで、最も低い周波数成分に相当する P0(P1)については、位置の情報をもたず、P2,P3,P4,P5 と周波数が高くなるにつれ、位置情報が付加され、その数が2のべき乗で増えることになる。
一般的な画像信号では、低域に大部分の電力が集中する。このため、P0 の絶対値が最も大きく、P1,P2,… と周波数が高くなるにつれ小さな値となる傾向がある。この性質を用いて、画像の圧縮が行われる。
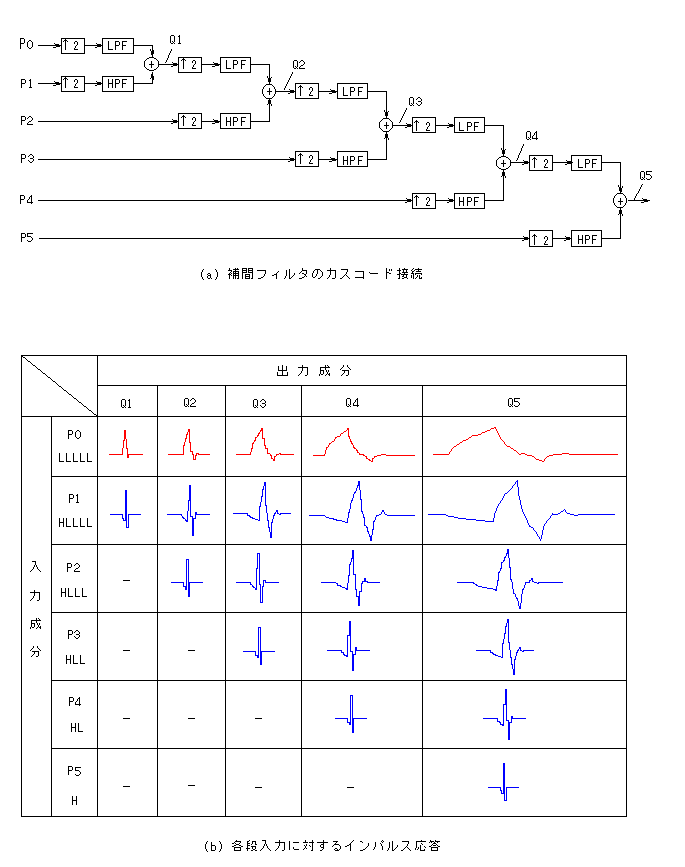
図13 補間フィルタのカスコード接続
[参考文献]
[1] 山田道夫:"ウェーブレット解析とその応用",信学論誌, Vol.76, No.5, pp.518-528, (May.1993)
[2] マーチン ヴェターリ:"ウェーブレット変換とサブバンド符号化”,信学論誌,Vol.74, No.12, pp.1275-1278,(Dec.1991)
[3] 山口昌哉:"カオス・フラクタル・ウェーブレット",数理科学, No.354, pp.5-10,(Dec.1992)
[4] 山田道夫:"ウェーブレット変換とは何か",数理科学, No.354, pp.11-17, (Dec.1992)
[5] 太田睦:"画像符号化における直交ウェーブレット",数理科学, No.354,pp.24-30,(Dec.1992)
[6] 守本晃:"ウェーブレット変換を用いた数値計算について",数理科学, No.354,pp.36-43,(Dec.1992)
[7] I.Daubechies: "The wavelet transform, time-frequency localization andsignal analysis",IEEE Trans.Information Theory,vol.36, pp.961-1004,(Sep. 1990)
[8] M.Antonini, M.Barlaud, P.Mathieu, I.Daubechies: "Image coding using wavelet transform",IEEE Trans.Image Process.,vol.1, pp.205-220,(Apr. 1992)
[9] M.Vetterli, C.Herley: "Wavelets and filter banks: theory and design",IEEE Trans.Signal Process.,vol.40, pp.2207-2232,(Sep. 1992)
[10] O.Rioul, M.Vetterli: "Wavelet and Signal Processing", IEEE SP Magazine,pp.14-38 (Oct.1991)
[11] S.G.Mallat: "A theory for multiresolution signal decomposition: The wavelet representation",IEEE Trans.Pattern analysis & Machine intelligence, vol.11, pp.674-693,(July 1989)
[12] S.G.Mallat: "Multifrequency channel decompositions of images and wavelet models",IEEE Trans.Acoust.,Speech & Signal Process.,ASSP-37, pp.2091-2110(Dec.1989).
[13] M.J.Shensa: "The discrete wavelet transform: wedding the A Trous and Mallat algorithms",IEEE Trans.Signal Process.,vol.40, pp.2464-2482,(Oct. 1992)
[14] 貴家仁志:"サブバンド符号化とウェーブレット変換",インターフェース,(Aug.1992)
[15] D.L.Gall, A.Tabatabai : "Subband coding of digital images using symmetric short-kernel filters and arithmetic coding techniques", IEEE ICASSP'88, pp.761-764 (June.1988)
[16] J.P.Princen et al.,: "Analysis/synthesis filter bank design based on time domain aliasing cancellation",IEEE Trans.Acoust.,Speech & Signal Process., ASSP-34, pp.1153-1161 (Oct.1986).
[17] R.E.Crochiere, L.R.Rabiner: "Multirate digital signal processing", Englewood Cliffs, NJ : Prentice-Hall (1983).
[18] J.B.Allen: "Short-time spectral analysis, synthesis and modification by discrete Fourier transform",IEEE Trans.Acoust.,Speech & Signal Process.,ASSP-25, pp.235-238 (June 1977).
[19] J.B.Allen, L.R.Rabiner: "A unified approach to short-time Fourier analysis and synthesis", Proc.IEEE, vol.65, pp.1558-1564 (Nov.1977).
[20] R.E.Crochiere: "A weighted overlap-add method of short-time Fourier analysis/synthesis",IEEE Trans.Acoust.,Speech & Signal Process., ASSP-28, pp.99-102 (Feb.1980).
[21] 井澤:"サブバンド符号化について",研究資料