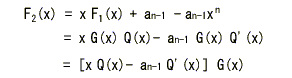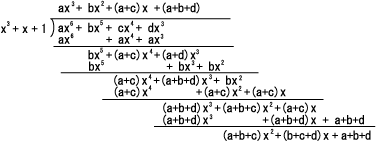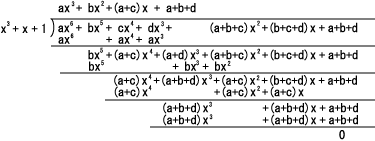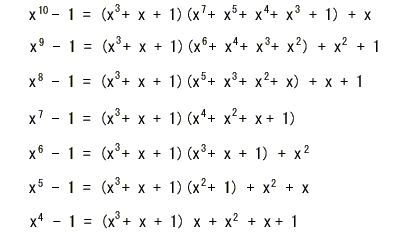巡回符号

誤り検出方式　－巡回符号－

井澤　裕司　　

1.　はじめに

ディジタル信号の伝送・記録では、1ビットの誤りが致命的な問題を引き起こす可能性
があります。
このため、フロッピーディスクやモデム、Ethernetなどのネットワークの分野では、これ
らの誤りを検出するため、巡回符号が用いられています。
いわゆるCRC（Cyclic Redundancy Checking）符号も、この巡回符号に属します。: 　
ここでは、巡回符号による誤り検出の原理と、その構成法について紹介します。

2.　定義

ディジタル信号は0と1の符号で表され、コンピュータ内部では2進数による四則演算が
用いられています。一方、誤り訂正（検出）符号の構成法を記述する場合には、
この2進数の演算とは異なる「modulo2」と称する演算が用いられます。
はじめに、このmodulo2の演算について説明しましょう。

2.1　modulo2の演算

modulo2の加算は次のようになります。

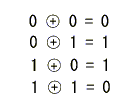
以下、表記の簡略化のため、単純にプラス(+)で表すことにします。

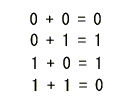
すなわち、mudulo2の加算は、桁上げという操作を伴わない2進数の加算に等価です。
　
次に、減算を定義するため、(-a) + a = 0 を満たす (-a) ［加算の逆元］を求めます。
上の加算の結果から、: 　

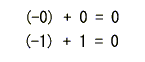
が得られ、

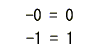
が成立します。
これより、modulo2 の演算では、加算（プラス+)と減算（マイナス-)の結果に違いはなく、
同じ結果になることがわかります。

一方、modulo2 の乗算は以下のようになります。
　

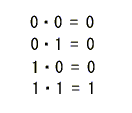
除算では、(a^-1) ・ a = 1 を満たす (a^-1) を求めます。
上の乗算の結果から、(1^-1) = 1 となり、a = 0 のとき (a^-1) は存在しないことがわかります。: 　
　
また、modulo2の変数 x を用いた多項式についても、以下のように加算、減算を行う
ことができます。
: 　
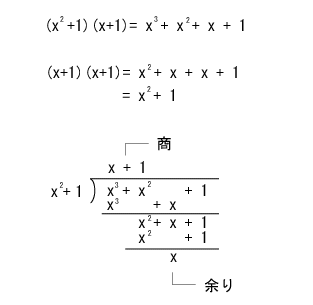
また、多項式におけるmodulo2の乗算と除算についても、次の例のように計算する
ことができます。

2.2　生成多項式とは

符号長がｎの符号語を（a₀, a₁, a₂, …, a_n-1）としたとき、これを変数 x の多項式 F(x)として
次のように表します。

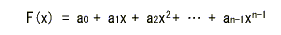
(n-1)次以下の多項式は全体で2ⁿ個存在しますが、その中でｋ次の特別な多項式 G（x) で
割り切れるものだけを符号として扱うことを考えます。
このF(x) を符号多項式、G(x) を生成多項式といいます。

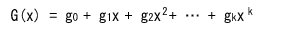
すなわち、符号長が nの符号多項式を F(x)、生成多項式 G(x) の次数を k とすると、

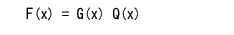
を満たす多項式 Q(x) の次数は（n-k-1）となり、Q(x) の総数は2^n-k となります。
個々のQ(x) について、それぞれ異なる符号多項式 F(x) が対応するので、F(x) の総数も
2^n-k となることがわかります。
すなわち、多項式Q(x) の各係数を（n-k）個の情報ビットに対応させることにより、
（n-k）個の符号語ができることになります。

2.3　巡回符号とは
　
xⁿ-1 が生成多項式 G(x) で割り切れるとき、このG(x) から生成される符号語を巡回状にシフトしたものも
また符号語になっています。（証明は後で示します。）
このような性質をもつ符号語を「巡回符号」といいます。: 　
2.2で述べたように、（n-k）個の情報ビットを係数とする多項式 Q(x) と、上で述べた巡回符号の
生成多項式 G(x) から、F(x) = G(x) Q（x) を計算することにより、巡回符号を作ることができます。
しかし、このようにして生成した符号の各ビットは、情報ビットとの対応がついていません。
そこで、次のように符号を構成することにより、符号ビットの特定の個所に情報ビットを対応させる
ことを考えます。

伝送するm（=n-k）個の情報ビットを係数とする多項式を P(x) で表します。
すなわち、次式が成立します。

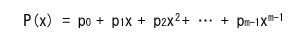
この多項式に x^n-m を乗じ、符号多項式の高次のｍ項に対応させます。
言うまでもなく、x^n-m ・P(x)　の低次の（n-m = k）項の係数はすべて０となります。
　
ここで、x^n-m ・P(x) を 2.2で示した生成多項式 G(x) で割り、その商を Q(x) 、余りを R(x) とします。
すなわち、: 　

　
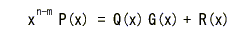
となり、余り R(x) の次数は（k-1）次以下になります。
いま、上式を変形すると次の式が得られます。

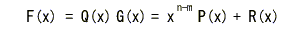
このようにすると、情報ビットは符号多項式の（n-1）次からｋ次までの係数としてそのまま扱うことができます。: 　
　
このような多項式 F(x)に対応する符号を伝送します。
なお、R(x) が k ビットの検査符号に相当します。

［証明］　巡回符号に関する定理

上で示した巡回符号に関する定理を証明しましょう。
いま、xⁿ-1が以下に示す F1(x) で割り切れるものとします。

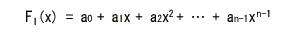
ここで F₁(x) について符号語を循環させた関数をＦ₂(x) とおくと、
以下のようになります。: 　

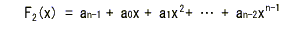
上の2式より、次の関係が成立します。
　

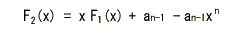
一方、xⁿ-1は G(x) で割り切れるので、その商を Q'(x) とおくと、
　

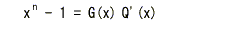
一方、 G(x) の定義より、
　

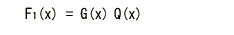
これより、次の関係式が成り立ちます。
　

　
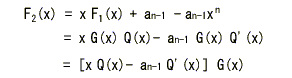
すなわち、循環変換した符号も符号語になっています。

3.　巡回符号の構成法

ここでは、具体的な巡回符号の構成法について説明します。
　
はじめに、送信側の手順を整理しましょう。: 　
(1)　伝送するm個の情報ビットから多項式 x^n-m ・P(x) を求めます。
　
(2)　上の多項式を生成多項式 G(x) で割り、その余り R(x) を求めます。

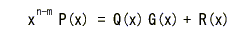
(3)　(1)の多項式 x^n-m ・P(x) と、(2)の余り R(x) の和 F(x) を求め、対応する符号を伝送します。
: 　
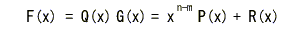
一方の受信側の手順は、以下のようになります。
　
(1)　送信された F(x) に伝送路で誤り E(x) が加わり、A(x) = F(x) + E(x) を受信したものと仮定します。

(2)　伝送された A(x) を生成多項式 G(x) で割り、その余り R(x) を求めます。
　
(3)　もし、伝送に誤りがなければ、A(x) は G(x) で割り切れるので、余り R(x) = 0 となります。
　　逆に、誤りがあると、余り R(x) ≠ 0 となります。

それでは、簡単な例について、実際に F(x) を計算してみましょう。
例えば、n=7，m=4　のとき、生成多項式として G(x) = x³+x+1 を用います。
伝送する情報ビットが (1,1,1,1) のとき、以下のように余りが求められます。:

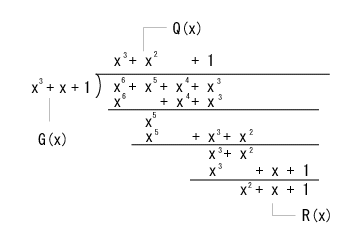
この余り R(x) は(1,1,1)の3ビットとなり、検査ビットといいます。
これより、伝送する巡回符号は　(1,1,1,1,1,1,1) となります。: 　
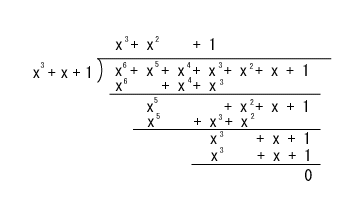
伝送路に誤りが生じなかった場合には、受信側ではA(x) = F(x) を受信します。
この A(x) を生成多項式 G(x) = x³+x+1 で割ります。
このとき、以下のように余りは０となり、誤りがなかったことがわかります。

　
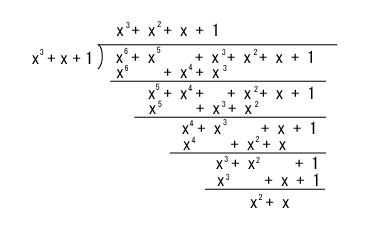
一方、伝送路で誤りが発生した場合ですが、例えば3ビットに誤りが生じ、(1,1,0,1,1,1,1)　という
符号が伝送されたものとします。
この場合は、次のように余り R(x) が０とならないことがわかります。

　
次に、これを一般化した4ビットの符号（a,b,c,d）について、巡回符号を求めてみましょう。
結果は、次のようになります。

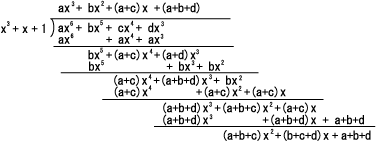
すなわち、求める F(x) は以下のようになります。
　
　
F(x) = ax⁶ + bx⁵ + cx⁴ + dx³ + (a+b+c)x² + (b+c+d)x + a+b+d

　
受信側では、この F(x) を生成多項式 G(x)で割ることにより、誤りの有無を調べます。
結果は以下のようになり、余りが０で、誤りがなかったことがわかります。:

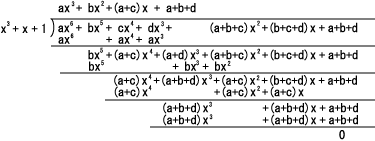
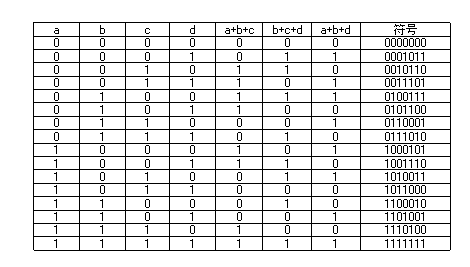
以上を、表の形に整理すると、以下のようになります。

　
この表から、この巡回符号の最小符号間距離は 3 であることがわかります。

4.　巡回符号の誤り検出: 　
次に、送信された符号のうちいずれか 1ビットに誤りがあった場合について考えてみましょう。
　
例えば、n=7，m=4　の例で整数 i　(0 ≦ i ≦6) とおくと、この単一誤りは E(x) = xⁱ で表されます。
このとき受信側の符号多項式は、
　
F(x) + E(x) = ax⁶ + bx⁵ + cx⁴ + dx³ + (a+b+c)x² + (b+c+d)x + a+b+d + xⁱ
　
となります。: 　
ここで、誤りの含まれない F(x) を G(x) で割った余りは 0 です。
したがって、｛F(x) + E(x) ｝を G(x) で割った余りは、E(x) を G(x) で割った余りに等しいことがわかります。
E(x) = xⁱ は G(x) を因数にもたないので、受信側の符号多項式が G(x)で割り切れないことは明らかです。
実際に、割り算をして確かめてみましょう。
　
・ x⁶/(x³+x+1) = x³+x+1 余り x²+1
・ x⁵/(x³+x+1) = x²+1 余り x²+x+1
・ x⁴/(x³+x+1) = x 余り x²+x
・ x³/(x³+x+1) = 1余り x+1
・ x²/(x³+x+1) = 0 余り x²
・ x/(x³+x+1) = 0 余り x
・ 1/(x³+x+1) = 0 余り 1
　
これらの余りの値はすべて異なっており、この値から誤ったビットの位置 [ i ] を求めることができます。
例えば、余りが（x²+1）のとき上式の a を反転させ、余りが（x²+x+1）のとき b を反転させれば、
誤りを訂正することが可能です。
　
次に、連続的な誤り（バーストエラー）が発生した場合について、検討してみましょう。
次数ｋの生成多項式 G(x)を用いて、巡回符号を構成したとき、連続する kビット以下の誤りを検出
することができます。
　
上の例（n=7、k=3）で確認してみましょう。
　
連続する3ビットの誤りのパターンを整理すると次の5種類になります。
　
・ x⁶+x⁵+x⁴ =x⁴ (x²+x+1)
・ x⁵+x⁴+x³ =x³ (x²+x+1)
・ x⁴+x³+x² =x² (x²+x+1)
・ x³+x²+x = x (x²+x+1)
・ x²+x+1 = 　x²+x+1: 　
これらは、3次の生成多項式、例えば G(x) = x³+x+1 で割り切れないことは明らかです。
　
次に、連続する2ビットではどのようになるでしょうか。
答えは、次の6パターンになります。
　
・ x⁶+x⁵ = x⁵ (x+1)
・ x⁵+x⁴ = x⁴ (x+1)
・ x⁴+x³ = x³ (x+1)
・ x³+x² = x² (x+1)
・ x²+x = x (x+1)
・ x+1 = x+1
　
これらについても、3次の生成多項式では割り切れません。
　
これを一般化し、生成多項式の次数を k とした場合について、連続する k ビット以下の誤りを
検出できることがわかります。

5.　巡回符号の回路構成

巡回符号を回路で実現する手法を紹介しましょう。
　
ここでは、上で説明した n=7, m=4, G(x)=x³+x+1の回路構成を示します。
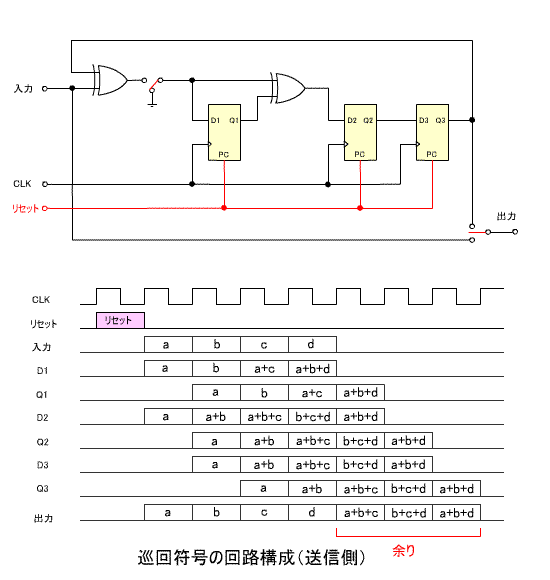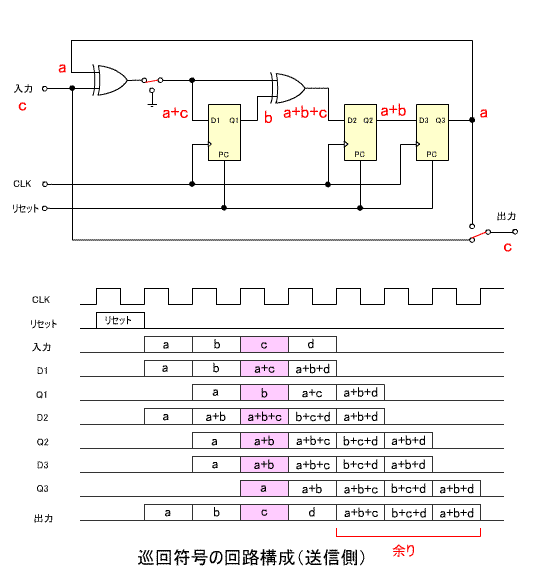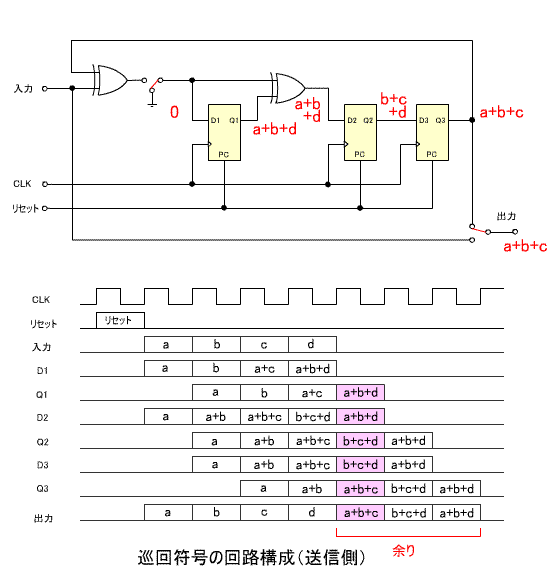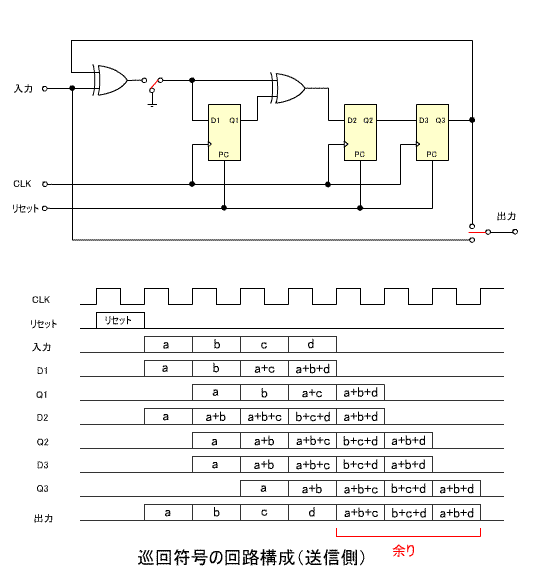
はじめに、送信側の構成です。
出力前半の4ビットは伝送する符号、後半の3ビットは余り R(x) に相当します。

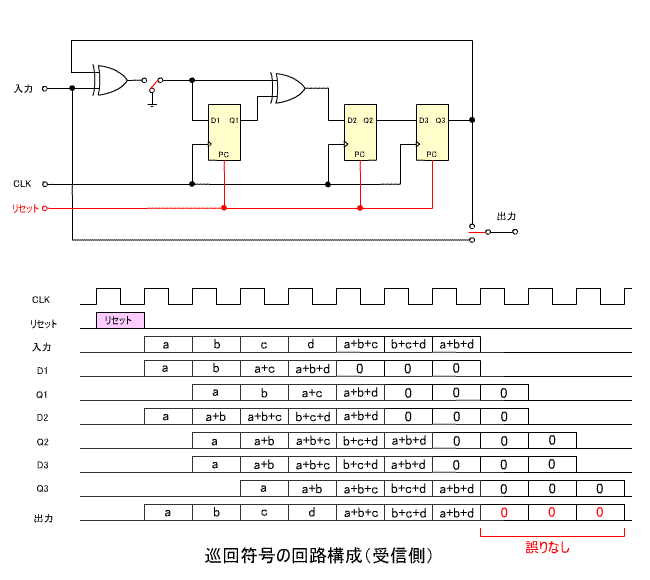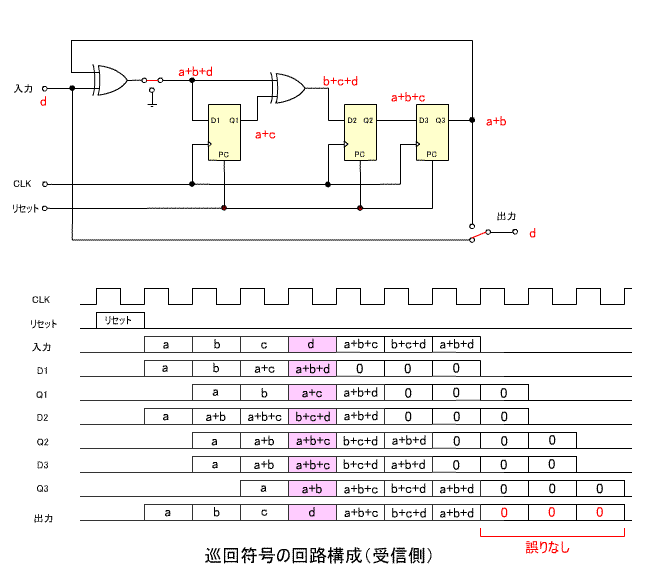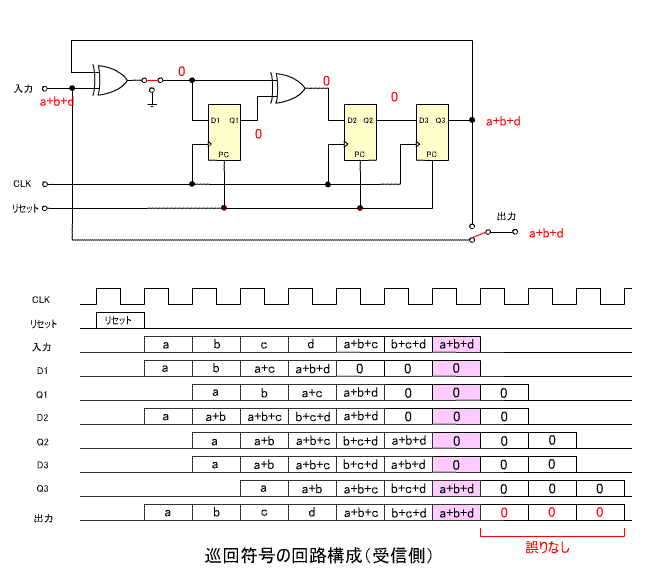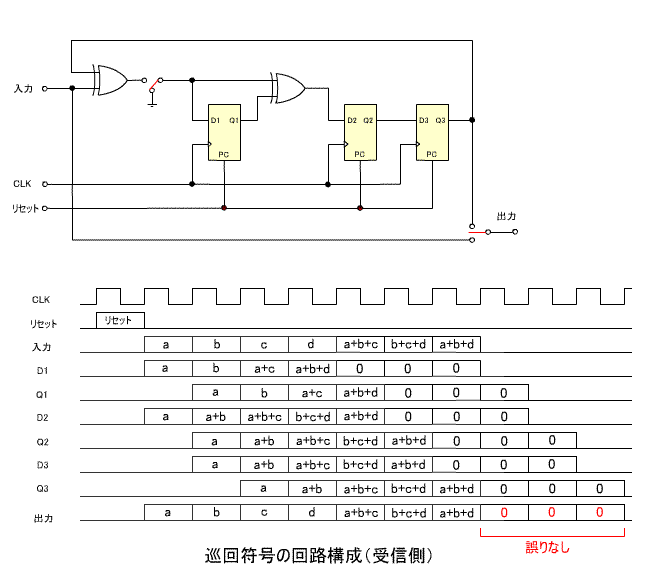
下の回路図は、受信側の構成です。
出力前半の7ビットは伝送された符号、後半の3ビットは余り R(x) に相当します。
この場合誤りがないので、余りはすべて０になります。

6.　CRC符号の構成法

前章では巡回符号により、符号誤りが検出できることを示しました。
巡回符号では、(xⁿ-1) が生成多項式 G(x) で割り切れることが条件となります。
しかし、任意の整数ｎに対して、G(x) がこのような条件を満たすとは限りません。
たとえば、生成多項式 G(x) = x³+x+1 について、調べてみましょう。
ｎが10から 4の場合について、(xⁿ-1) を G(x) で割ると次のようになります。

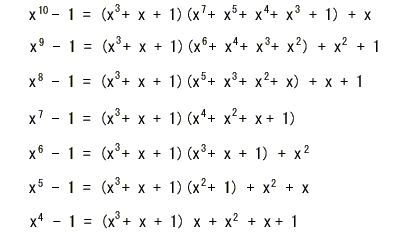
これより、G(x) = x³+x+1の場合、10以下の n について巡回符号となるのは、n = 7 の場合
のみであり、それ以外では巡回符号が構成できないことがわかります。: 　
実際には、アプリケーションにより様々なビット数の誤り検出符号が必要となります。
そこで、短縮化巡回符号という方式が考案されました。
これを、CRC（Cyclic redundancy Checking）方式と呼びます。
　
この方式は、xⁿ-1が生成多項式 G(x) で割り切れない場合は、 G(x) で割り切れる(n-1)次以下
の多項式を用いるというものです。
　
例えば、上の例で、n=6 、G(x) = x³+x+1の場合について検討してみましょう。
G(x) で割り切れる5次以下の多項式は以下の８つです。
　
・　0
・ x³+x+1
・ (x³+x+1) x = x⁴+x²+x
・ (x³+x+1)(x+1) = x⁴+x³+x²+1
・ (x³+x+1) x² = x⁵+x³+x²
・ (x³+x+1)(x²+1) = x⁵+x²+x+1
・ (x³+x+1)(x²+x) = x⁵+x⁴+x³+x
・ (x³+x+1)(x²+x+1) = x⁵+x⁴+1: 　
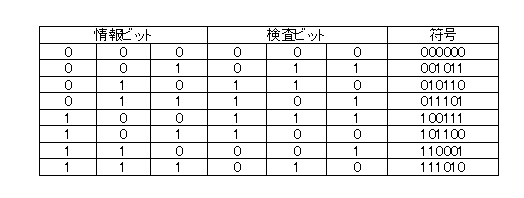
したがって、最終的な符号は次の表のようになります。
　

　
実は、この表は巡回符号の n=７、G(x) = x³+x+1の表の上半分（すなわちMSBが0）に対応しています。
　
一般には、次に示す生成多項式が用いられています。
　
　
(1)　CRC-CCITT: 　
　　　G(x) = x¹⁶+x¹²+x⁵+1
　
(2) CRC-16
　
　　　G(x) = x¹⁶+x¹⁵+x²+1
　
(3) CRC-12
　
　　　G(x) = x¹²+x¹¹+x³+x²+x+1
　
　
これらの詳細については、文献等で調べて下さい。

7.　まとめ

データの誤りを検出する手法として、巡回符号を紹介し、その構成法について解説しました。
実際にモデム等で使用されているCRC符号は、ビット反転等の前処理・後処理が用いられています。
その詳細については、参考文献等で調べて下さい。

［参考文献］
　
[1]南敏著、情報理論，産業図書
[2]松本光功他著、コンピュータ回路，森北出版
[3]今井秀樹著、情報理論、昭晃堂
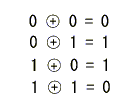
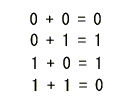
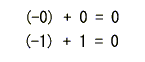
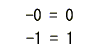
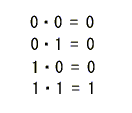