2010.12.15 first editions
(related item: principle of equivalence, inertial mass)
Both of momenta and kinetic energy increase with the time process in accelerated motion, though they are constant in uniform motion. In accelerated motion, I think I want to clarify the mechanism to get both of momenta and kinetic energy. In the space which doesn't include any nearby star,etc which causes gravitational field, it is assumed there is object m then, we think about a minute part delta-m of object m. (Figure-1)
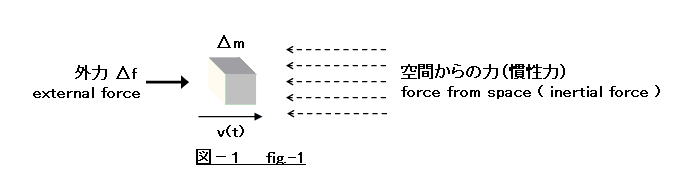
It moves at speed v(t) according to external force delta-f. Then, the force that delta-m receives from space is delta-f. (inertial force)
Limitation to consideration: It is limited to the shower of neutrino from backward and from forward in axis, as typical case where axial element of momenta becomes maximum. (Figure-2)
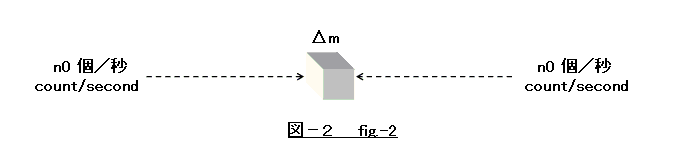
Hereafter, it explains in detail by the track of time-coordinate and x-coordinate of delta-m.
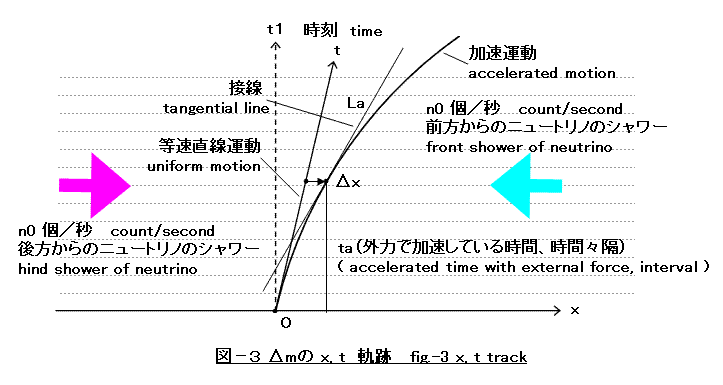
X coordinate increases with time process. Then, even if shower from forward has been generated at n0 pieces per second, timing that reaches delta-m becomes early little by little.
Uniform motion is approved where neighborhood is uniform at least, and doesn't receive biased force from back and forth in space. Acceleration motion can be considered based on uniform motion. Brake force is generated in the accelerated motion, because it parts increasingly from base line (uniform motion) and it advances. Brake force is balanced to the delta-f of external force, where delta-f pushes against delta-m.
After time ta that is accelerated by external force, tangent La becomes new base line of uniform motion.
In the case of uniformly accelerated motion, the track in x-t coordinate describes a parabola.
x = B(t - t0)(t - t0)/2 + x0 ----- parabola
x' = B(t - t0) ----- speed
x'' = B ----- constant acceleration
Ta in figure is time interval as it is. Divide time axis one after another with short time interval ta of constant. Choose an interval arbitrarily. Mark both of starting point p and ending point q of the track of corresponding to that interval. The coordinate of point q is q(Xq,Tq). Xpq is x coordinate of Lp of corresponding to Tq. Delta-x is difference between Xpq and Xq.
As for track of parabola, the delta-x corresponding to time interval ta is constant at any time. ----- (1)
x = f(t) = B(t - t0)(t - t0)/2 + x0
It is possible to explain with taylor expansion.
f(t0 + ta) = f(t0) + f '(t0)*ta + f ''(t0)*ta*ta/2
'1st section + 2nd section' of right side is equation of tangential line that is tangential to the track at time t0. 3rd section of right side is above-mentioned delta-x.
delta-x = f ''(t0)*ta*ta/2
Substitute next parabolic equation for this.
f '' = X '' = B
delta-x = B*ta*ta/2
Delta-x doesn't depend at time t0 and is constant. ----- Proof end of (1)
Therefore, the brake force (= external force) is thought to occur by delta-x, and is constant at any section of time axis. This means that the brake force is constant at any time, where track is parabola. Here, though the force synchronizes with ta and will change, suitable ta corresponding to actual force in space will be found.
summary
About the theory that inertial force originates from neutrino (or such particle) that runs in all directions in space, I explained only the point in hasty.
it returns.
.