2010.12.15 初版
(関連項目:等価原理、慣性質量)
等速直線運動は、運動量一定、運動エネルギー一定だが、加速運動では時間経過とともに運動量増加、運動エネルギー増加となる。加速運動における運動量および運動エネルギーを獲得する仕組みを明らかにしたい。近くに重力を及ぼす星などがない宇宙空間において、物体mがあるとして、物体mのある微小部分 Δm について考える。(図−1)
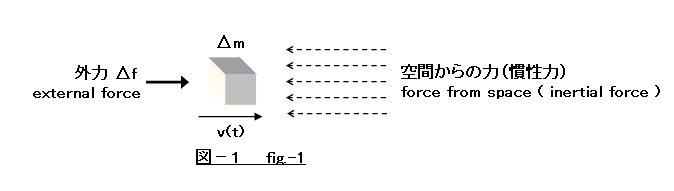
外力 Δf により速度 v(t) で動く。このとき Δm が空間から受ける力は、Δf そのものである。(慣性力)
考察限定:運動量の軸方向成分が最も大きくなる代表的ケースとして、軸上の前方および後方からのニュートリノのシャワーに限定する。(図−2)
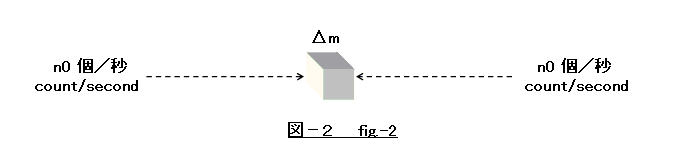
ここから先は、Δm の x, t 軌跡によって詳しく説明する。(図−3)
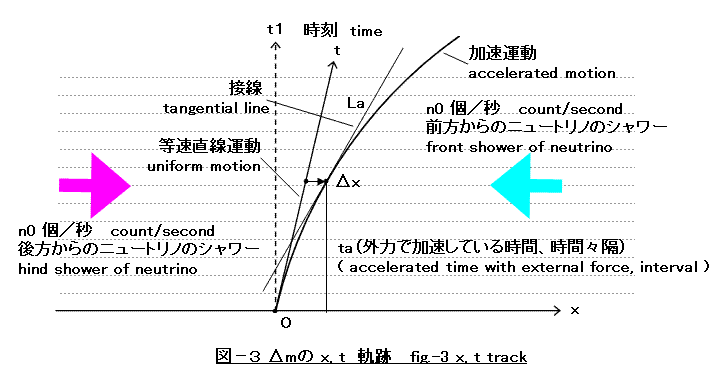
時間経過とともに x 座標が増えていく。すると前方からのシャワーは n0 個/秒で発生していても、Δm に届くタイミングが少しずつ早くなる。これは単位時間当たりの Δm へのシャワーが増えたことになる。そのため前方からの圧力(ブレーキ)は増える。反対に後方からの圧力(アクセル)は減るため、ブレーキ力は2倍化する。
等速直線運動は、宇宙空間が少なくとも近傍では一様であることによって成立するものであり、空間からの前後方向の偏った力を受けない。等速直線運動を基準にして、加速運動を考察できる。加速運動では、時間とともに基準(等速直線運動)からどんどん離れて進んで行くので、ブレーキ力が発生する。そのブレーキ力は Δm を押す外力 Δf と釣り合う。
外力によって加速している時間 ta の後には、接線 La が新たな等速直線運動の基準になる。
等加速度運動の場合は、x, t 座標上の軌跡は放物線を描く。
x = B(t - t0)(t - t0)/2 + x0 .... 放物線
x' = B(t - t0) ...................速度
x'' = B ..........................加速度一定
図の ta をそのまま時間々隔とする。時間軸を適当な単位時間々隔 ta で次々と区切る。ある区間の始めの接線と、ta 時間後の軌跡との x方向のずれを Δx とする。
軌跡が放物線の場合は、どの時刻においても、時間々隔 ta に対する Δx は一定である。 ....(1)
x = f(t) = B(t - t0)(t - t0)/2 + x0 として、テーラー展開することによって説明できる。
f(t0 + ta) = f(t0) + f '(t0)・ta + f ''(t0)・ta・ta/2
1項目+2項目は、時刻 t0 で接する接線の式である。その接線と、時刻 t0 + ta における放物線との x 方向のずれを Δx とすると、3項目が Δx となる。
Δx = f ''(t0)・ta・ta/2
これに放物線の式 f '' = X '' = B を代入すると、
Δx = B・ta・ta/2
Δx は、時刻 t0 によらず一定である。 ....(1)の証明終り
よって、Δx によって起こると考えられるブレーキ力( = 外力 )は、時間軸上のどの区間でも一定である。このことは、軌跡が放物線の場合、空間からのブレーキ力( = 慣性力 Δf )は時間によらず一定であることを意味する。ここで、ta の値の大小に連動して力の大きさが変ってしまうことになるが、空間での実際の力に見合う ta の値があるものと考えられる。
まとめ
慣性力は、宇宙空間を縦横無尽に走行するニュートリノ(又はそのような粒子)に起因するという説について、要点のみはしょって説明した。
戻る
.