2009.12.26版

重力原因物質として適しているニュートリノ
　ニュートリノは、静止質量がきわめて小さくて、光速で直進し大きな運動エネルギーを持つ。

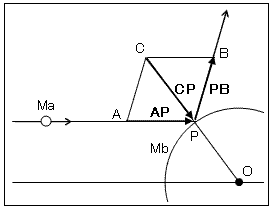　 図は、重い物体Ｍbに対して質量極小の物体Ｍaが弾性衝突する場合の運動量の関係を示しています。 Ａ方向から飛んで来たＭaはＰ点で弾性衝突して法線ＯＣ対称のＢ方向に行きます。 Ｍbは重いので衝突で運動量を貰ってもほとんど動きません。
それを踏まえて、エネルギー保存と運動量保存の両法則について考察します。 まず、Ｍbは動かないので受け取る運動エネルギーはゼロです。 するとエネルギー保存の法則から、Ｍaは衝突前の運動エネルギーを衝突後もそのまま保持します。 ということは、衝突前後でのＭaの運動量の絶対値も変化しません。 運動量は大きさと方向を持つベクトルです。 衝突前後では運動量ベクトルは図のような平行四辺形の関係になっていて、 Ｍbが法線方向に大きな運動量ベクトルを受けます。
ここで、ベクトルＡＰとＰＢは、衝突前後のＭaの運動量です。 ベクトルＣＰは、衝突によってＭbが受ける運動量です。 運動量保存の法則から、衝突前後でＡＰ＝ＣＰ＋ＰＢとなります。

この衝突での着眼点：
Ｍaは、運動エネルギー不変、運動量の絶対値も不変。
Ｍbは、受取るエネルギーが発生せずに大きな運動量を貰う。 運動量は力の元になりますが、エネルギーによる発熱等がありません。

なお、Ｍbの質量が無限大ではなくＭaよりも数桁大きい弾性衝突は、ニュートリノによる重力理論の根幹のようです：
Ｍaは、運動エネルギーの一部を失う、運動量の絶対値も少し小さくなる。
Ｍbは、受取るエネルギーが発生する。大きな運動量を貰うことには変わりがない。 運動量は力の元になりますが、エネルギーによる若干の発熱等もある。


ニュートリノの弾性衝突による重力理論が浮かんでくる！
宇宙空間に大きな物体Ｍがあって、宇宙のあらゆる方角からニュートリノが降り注ぐものとします。 ニュートリノの大部分は何事もないかのように透過します。 一部のニュートリノはＭと弾性衝突して宇宙の方に戻って行きますが、 運動エネルギーの一部を失って運動量の絶対値も少し小さくなっています。
つまり、ニュートリノのエネルギーは宇宙からＭに向かうのと 逆方向のＭから宇宙に向かうのとでは後者が小さくなっています。 非常に多数の似たような衝突があらゆる方向に均一に起こることによって、 Ｍに向かう重力場が生じるということになります。

逆２乗の法則…
物体Ｍから離れたある位置で、軸と直角方向の単位面積・単位時間に通過する物体Ｍで撥ね返った粒子数については、多い所（物体Ｍに近い所）は重力が大きく、少ない所（物体Ｍから遠い所）は重力が小さくなります。重力の大きさはその粒子数に比例します。物体Ｍで撥ね返った粒子は全方向一様として、単位面積・単位時間での通過数は物体Ｍからの距離の２乗に反比例します。すなわち重力の逆２乗の法則に他なりません。


重力場の感知
まず、宇宙空間に１つだけ質点があって他には物体が無い場合を考えます。質点は、全方向から来て質点と弾性衝突する微小粒子により個々には大きな運動量ベクトルを受けますが、全方向均一のため総和は０ベクトルです。互いに反対向きのベクトルが打ち消し合っているとも言えます。この場合は、質点は特定の向きに引力を受けません。

次に、質点および重力場を発生している物体があるとします。質点が受ける個々の運動量ベクトルについては、物体の方角から来る粒子によるものは衝突でエネルギーを少し失って絶対値が小さくなっています。そのため質点位置において方角による運動量のバランスが崩れて引力が発生します。互いに反対向きの２つの大きな運動量は、一方が少し変わるだけで大きな差となります。すなわち重力場の中において、質点は粒子の持つ運動量のわずかの差を効率よく感知して引力に換えていると考えられます。


戻る



.