apx.244a. ポアソン分布   目次（第5章）へ

　ポアソン分布( Poisson distribution )は，二項分布で平均 n p = mを一定とし，p → 0としたときの極限の分布である．したがって希現象の生起回数の確率として有用である．ここで，二項分布とは，毎回の試行において事象Eの起こる確率を pとするとき，n 回の独立試行中に事象Eが x 回起こる確率のことで，

(ｘ= 0，1，…，n)である．

　平均 ｍ 回起こるはずのところが，ちょうどｘ回だけ起こる確率Ｐ(x)は，

　　　　　　　　　ｘ＝0，1，…，ｍ，…

で与えられる．このとき平均 ｍ，分散 mである．

　図5.8左は m = 1または 2の場合のポアソン分布である．

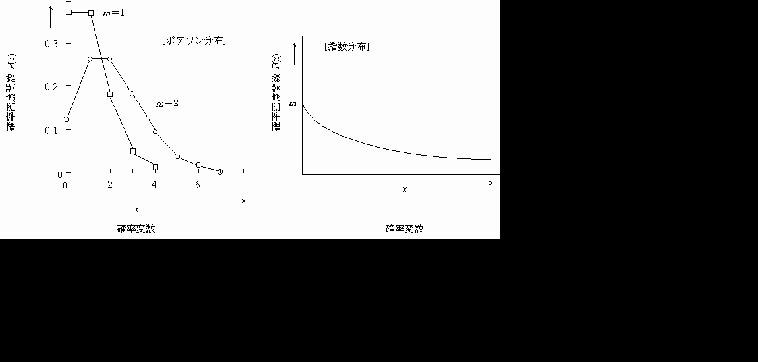
図 5.8　ポアソン分布と指数関数

　［例］　あるライスセンターは平均10回 / 時の籾の荷受けを行うが，1時間に荷受けできる最大回数は20であるという．このライスセンターで，1日 ( 10時間 ) の間に負担過重の生ずる確率を求めよ．

　籾の到着はポアソン分布に従うものとすれば，m = 10として1時間にK回の籾の到着の生ずる確率Ｐ(k) は

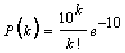
である.したがって1時間に生ずる籾の到着回数が20以下である確率はであり，10時間引続いて，毎時の到着数が20以下である確率はで表 される．求める確率は

と得られる．