図
5.1 入札額と利益5.2 演習問題解答
第２章 目次（第5章）へ
2.3.3 各自試みよ．
2.4.1 入札額と利益
牛A |
牛B |
|
X |
ｘ |
100−x |
Y |
ｙ |
100−y |
ＸがＡへ x万円，ＹがＡへ y万円入札したとすると，x ＞ yのときＡはXに，ＢはＹに落札されるから，Ｘの利益は，80− x Ｙの利益は，60− (100−y)＝ y−40
x＜ yのときＢは x に，Ａは y に落札されるから，
Ｘの利益は，60− (100−x)＝ x−40
Ｙの利益は，80− y
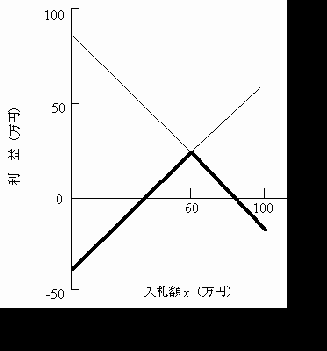
したがって，Ｘ氏は利益のミニマックス， Ｆ＝max min (80−x ，x−40） をとればよい．
min (80−x ，x−40)は下図1の太線で示され，その最大値はF＝20万円で，x＝60万円である．すなわち，Ｘは牛Ａに60万円，牛Ｂに40万円を入札すればよい．
図
5.1 入札額と利益
2.4.2 1) ｑ＝（0.4 0.6）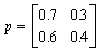 
q (2)＝q・p 2＝（0.664 0.336） X：66.4％
2) 不動確率ベクトル t を用いて
t1 ＋ t2 ＝ 1
両式からt1 = 2 / 3 , t2 = 1 / 3 したがって，X，Yの栽培農家は，66.7％，33.3％
2.4.3.1 近似値＝0.746
2.4.3.2 晴天率＝約0.8，雨天率＝約0.2，２日以上連続雨天の回数約15回．附録にプログラムと計算例を示す．
●ソフトウェア mc_wethj.exe
2.4.3.3 初日の天候を晴（Ｘ＝１）とし，一様乱数Ｒを用いて，晴になる日は，Ｒ＜Ａ，曇になるのは，Ａ≦Ｒ＜Ａ＋Ｂ，雨になるのはＡ＋Ｂ≦Ｒ≦１とすると，フローチャートは，図5.2のようになる．
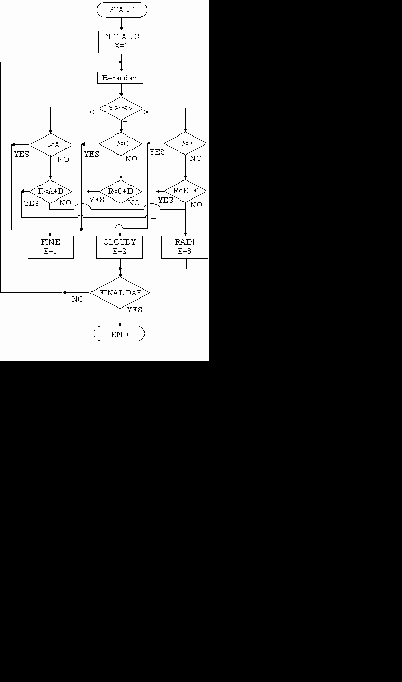図 5.2 天候フローチャート
2.4.4 平均到着数λ= 3，平均処理回数μ= 5であるので，入荷率ρ＝λ／μ＝３／５である．
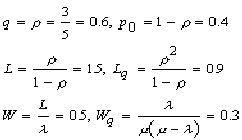
λ＜μであるから荷口が等間隔で到着する場合は待たされることはないが，ランダムに到着する場合は平均18分 (Wq) 待たされ，平均 0.9の荷口行列ができるといえよう．
2.5.2.1 x ＝ 6，y＝5，z＝36
2.5.2.2 x = 8 / 13 = 0.615, y = 27 / 13 = 2.077, z = 110+3/13 = 110.231
2.5.2.3 各自試みよ．
2.5.3 1) 10 x＋15 y ≦ 5,000 3 x＋ 5 y ≦ 1,000 7 x＋ 3 y≦ 800 のもとで，
z＝1200 x＋700 yを最大にせよ．
2) ，3) 各自試みよ． x＝38.46 kg y＝176.92 kg z＝170,000円
2.5.4 1 - 2 - 3 - 4 - 5で，17日かかる．
2.5.5.1 AEFGKLP = 23時間．
2.5.5.2 各自試みよ．
2.6.2.1 0.9896
2.6.2.2 各自試みよ．
2.6.3.1 X＋X・Y＝X・（1＋Y）＝X
X・（X＋Y）＝X・X＋X・Y＝X＋X・Y＝X
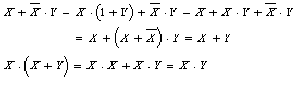
2.6.3.2
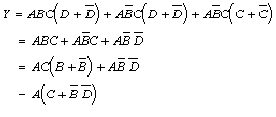
2.6.3.3 図5.3
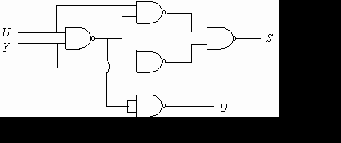図
5.3 半加算器の回路
2.6.3.4 Lに関する真理値表は，つぎのとおりである．
Ｘ |
Ｙ |
Ｚ |
Ｌ |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
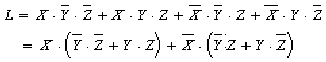
回路図は，図5.4のとおりである．
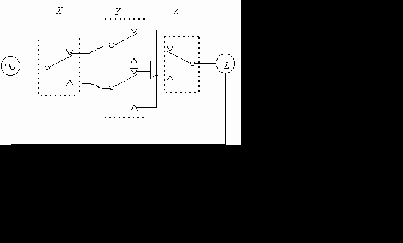図
5.4 ３カ所から点滅回路
2.6.3.5 IC：NE555 のピン配置図を図5.5（左）に示す．
これを図5.5（右）のように結線して，ピン2のトリガーにLOWパルスを加えると，時間 t ( =1.1･R･C )の長さのHIGHパルスがアウトプットピン3に得られる．
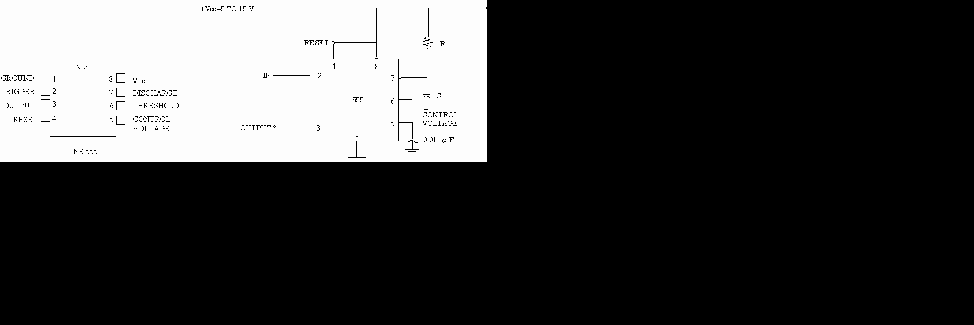
図 5.5 タイマーIC（NE555）（左）とディレー信号発生回路（右）