3.3.2 地域用水利用計画への応用 目次(第3章)へ
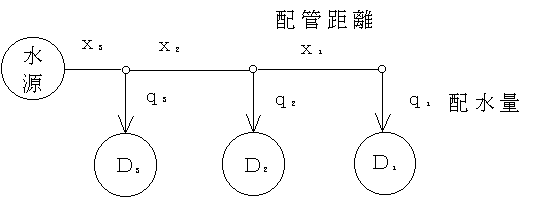
図3.9のように,3地区( D1 D2 D3 )の受益地が一本の用水路にそっている地区の用水配分の最適化への応用を考えてみよう.ただし,水源からの年間供給可能水量Qは7(×106) m3,それぞれの地区の年間配水量をq iとすると,各地区の年利益v i = k i q i百万円,( k1= 24,k2= 15,k3=7 )であり,水路経費Ci= xi(q+1)2百万円であり,ここで,x1= 2,x2= 1,x3= 0.5(km)のとき,全利益から用水路の全経費を引いた値Bを最大にすることとする.

図 3.9 農業用水配分
この問題は,
![]() ≦Q eq. 3.9
≦Q eq. 3.9
のもとで
![]() eq. 3.10
eq. 3.10
を求めることである.
まず,D 1では,実際の利用水量をq1とすると,純益F1(q)は,
F 1(q) = v 1(q)−C 1(q)
= k 1 ・ q 1− x 1 ・(q +1)2 eeq. 3.11
∴ f 1(q) = max F 1(q)
= max[k 1・ q 1 − x 1・(q +1)2] eq. 3.12
0 ≦ q 1 ≦ q ≦ Q eq. 3.13
また,D 2地区の純益F 2(q)は,
F 2(q)= k 2 ・ q 2 − x 2 ・(q + 1)2 eq. 3.14
D 1 , D 2 ,両地区の最大純益は,
∴ f 2(q)= max[F 2 (q)+f1(q − q2)]
= max[k 2 ・ q 2 − x 2・(q + 1)2 + f 1(q − q 2 )] eq. 3.15
同様に,D 3地区の純益はF 3 (q)は,
F 3(q)= k 3 ・ q 3 − x 3 ・(q +1)2 eq. 3.16
∴ f 3(q)= max[F 3 (q)+f 2(q − q 3)]
= max[k 3 ・ q 3 − x 3 ・(q + 1)2 + f 2(q − q 3)] eq. 3.17
i) 配水量qと利益v・水路経費との関係が表で示された場合
表3.3 用水配分( D1地区 )
配水量 |
D1地区の利益 |
D1の水路経費 |
純益 |
最適配分 |
q |
k1q1 |
x1(1+q)2 |
f1(q) |
q1 |
1.0 |
24 |
8 |
16 |
1.0 |
1.25 |
30 |
10.125 |
19.875 |
1.25 |
2.0 |
48 |
18 |
30 |
2.0 |
3.0 |
72 |
32 |
40 |
3.0 |
4.0 |
96 |
50 |
46 |
4.0 |
5.0 |
120 |
72 |
48* |
5.0 |
6.0 |
144 |
98 |
46 |
5.0 |
7.0 |
168 |
128 |
40 |
5.0 |
×10 6 m3 |
×10 6円 |
10 6円 |
×10 6円 |
×10 6円 |
f 1 (q) は,表3.3のように凸関数でありq = 5のとき最大値4,800万円を示す.つづいて,表3.4のようにf 2 (q ,q 2)を計算し,qに対する*印の最大純益が求められる.表3.5で,q = 6が用水路のD 3地区の上流で利用可能のときの最大純益は2,662.5万円で,D 3地区にq 3 = 3.0を配分し,残りのq − q 3 = 3.0をD 1,D 2地区に配分することになる.この配分は,表3.4のq = 3.0の最適配分からq1= 1.25,q2= 1.75,が得られる.さらに,表3.5でf 3 (q,q 3)は,q = 6.0のとき最大値2,662.5万円を示し,本用水配分システムでは,表3.6のように,D 1地区に1.25,D 2地区に1.75,D 3地区に3.0(×10 6 m 3)を配分するのが最適であることが得られ,Q = 7では用水があまることになる.
ii) 配水量qと純益F(q)が関数関係で示されている場合
D 1地区では,配水された用水量qを全部利用するときに純益は最大になるので,
F1(q,q1)= k 1・ q 1 − x 1・(q + 1)2
= 24q 1 − 2(q+1)2 eq. 3.18
において,q 1 = qである.
表3.4 用水配分(D 2,D 1地区)
| 配水量 | D2への配水 | D1への配水 | D1の純益 | D1の利益 | D2 の水路経費 | 純益 | 最適配分 |
q |
q2 |
q -q2 |
f1 (q-q2) |
k 2 q 2 |
x 2 (1+q) 2 |
f 2 (q , q 2 ) | |
1 |
0 |
1 | 16 | 0 | 4 | 12* | q1= 1.0 |
1 |
0 | 0 | 15 | 4 | 11 | q2=.0 | |
2 |
0 |
2 | 30 | 0 | 9 | 21 | |
| 0.75 | 1.25 | 19.875 | 11.25 | 9 | 22.125* | q1= 1.25 | |
1 |
1 | 16 | 15 | 9 | 22 | q2=0.75 | |
2 |
0 | 0 | 30 | 9 | 21 | ||
3 |
0 |
3 | 40 | 0 | 16 |
24 | |
1 |
2 | 30 | 15 | 16 |
29 | ||
| 1.75 | 1.25 | 19.875 | 26.25 | 16 |
30.125* | q1=1.25 | |
2 |
1 | 16 | 30 | 16 |
30 | q2=1.75 | |
3 |
0 | 0 | 45 | 16 |
29 | ||
4 |
0 |
4 | 46 | 0 | 25 |
21 | |
1 |
3 | 40 | 15 | 25 |
30 | ||
2 |
2 | 30 | 30 | 25 |
35 | ||
3 |
1 | 16 | 45 | 25 |
36* | q1=1.0 | |
4 |
0 | 0 | 60 | 25 |
35 | q2=3.0 |
∴ f 1(q) = max F 1(q , q 1 )
= max [24 q−2(q+1)2 ] eq. 3.19
0<q<Q =7 eq. 3.20
これは,d f i(q)/dq = 0とおき,24 − 4(1+q)= 0,ゆえにq = 5のとき,f 1(q)は最大値48となる.
つぎに,用水量qをD 2 地区でq 2 だけ利用したときのD 2 地区の純益は,
F 2(q,q 2 )= k 2 ・ q 2 − x 2 ・(q+1)2 eq. 3.21
また,D1地区では q−q 2 だけ配水されるので,D1,D2両地区の利益合計f 2( q,q 2 )は,
f 2(q,q 2)= F 2( q,q 2 )+f 1(q− q 2 )
= k 2 ・q 2 − x 2 ・(q+1)2+24 (q− q 2)−2 (q− q 2 +1)2
=15q 2 − (q+1)2+24 (q− q 2) −2(q− q 2 +1)2 eq. 3.22
=−2q 2 2 + [4(q+1)−9] q 2−3(q+1)2 + 24q
表3.5 用水配分(D 3 ,D 2 ,,D 1地区)
| 配水量 | D3への配分 | D2 D1の配分 | D2 D1の純益 | D3の利益 | D3の水路経費 | 純益 | 最適配分 |
q |
q3 |
q -q3 |
f2 (q-q3) | k3 q3 | x3 (1+q) 2 |
f3 (q , q 2 ) | |
3 |
0 |
3 |
30.125 | 0 | 8 | 22.125 | q1=1.25 |
1 |
2 |
22 | 7 | 8 | 21 | q2=1.75 | |
2 |
1 |
12 | 14 |
8 | 18 | q3=0 | |
3 |
0 |
0 | 12 |
8 | 13 | ||
4 |
0 |
4 |
36 | 0 | 12.5 |
23.5 | q1=1.25 |
1 |
3 |
30.125 | 7 | 12.5 |
24.625 | q2=1.75 | |
2 |
2 |
22 | 14 |
12.5 |
23.5 | q3=1.0 | |
5 |
1 |
4 |
36 | 7 | 18 | 25 | q1=1.25 |
2 |
3 |
30.125 | 14 |
18 | 26.125 | q2=1.75 | |
3 |
2 |
22 | 21 |
18 | 25 | q3=2.0 | |
6 |
2 |
4 |
36 | 14 |
24.5 |
25.5 | q1=1.25 |
3 |
3 |
30.125 | 21 |
24.5 |
26.625* | q2=1.75 | |
4 |
2 |
22 | 28 |
24.5 |
25.5 | q3=3.0 | |
7 |
3 |
4 |
36 | 21 |
32 | 25 | q1=1.25 |
4 |
3 |
30.125 | 28 |
32 | 26.125* | q2=1.75 | |
5 |
2 |
22 | 25 |
32 | 25 | q3=4.0 |
表3.6 最適用水配分
供給可能水量 q (×10 6 ) m 3 |
D 1への配水 q 1 |
D 2への配水 q 2 |
D 3への配水 q 3 |
最大純益 f 3 (q)万円 |
3 |
1.25 |
1.75 |
0 |
2212.5 |
4 |
1.25 |
1.75 |
1 |
2462.5 |
5 |
1.25 |
1.75 |
2 |
2612.5 |
6 |
1.25 |
1.75 |
3 |
2662.5* |
7 |
1.25 |
1.75 |
3 |
2612.5 |
ここで,d f 2 (q,q 2 ) /d q 2 =−4q 2 +[4(q+1)−9] = 0 とおくと
q 2 = q−1.25 eq. 3.23
したがってD1 D2 全体の最大利益は,f 2( q ,q 2 ) に(3.23)を代入して,
f 2(q)= max f 2(q,q 2 )
=−q 2 +13 q+ 0.125 eq. 3.24
これは,d f 2(q)d q = 0とおくと,q = 6.5,したがってf 2(q)は,そのとき最大値42.375となる.
同様に,用水量qをD 3地区でq 3 だけ利用したときのD 3 地区の純益は,
F 3(q,q 3 )= k 3・ q 3 − x 3(q+1)2 eq. 3.25
また,D 1 ,D 2 地区へはq−q 3だけ配水されるので,D 1 ,D 2 ,D 3地区の利益合計f 3(q ,q 3)は,
f 3(q,q 3 )=F 3(q,q 3 )+f 2(q−q 3 )
=k 3・q 3 − x 3(q+1)2−(q−q 3)2+13(q−q 3)+1.25
=7q 3 − 0.5(q+1)2−(q− q 3)2+13(q− q 3)+1.25 eq. 3.26
ここで,d f 3(q,q 3 )/d q 3 = 0 とおくと
q 3 = q−3, eq. 3.27
したがってD 1,D 2,D 3全体の最大利益は,f 3 (q,q 3)に式 (3.27) 式を代入して
f 3(q)= max f 3(q,q 3 )
=− 0.5 q 2 + 6 q+8.625 eq. 3.28
これはd f 3(q)/d q = 0とおくと,q = 6,このときf 3(q)は,最大値26.625となる.また最適配水量は,(3.27),(3.23) ,(3.18)式より,q 3 = 3,q 2 = 1.75,q 1 = 1.25である.