3.2.2　農作業計画への応用　　　 目次（第３章）へ

　農業への応用例としては，作付体系の計画，農業経営の改善等などがあるが，ここでは，最も簡単な作業日程計画への応用例について述べる．

　〔例題〕　作業期間が異なる組作業

　図3.8において，作業1, 2は，作業可能日が一部重複していて同時に二作業はできないので，その複合負担面積は，次式で求められる．

　　　　　　　　eq. 3.2

ここで，

　　S：全作業可能時間 （h）

　　S₁：作業1の作業可能時間 （h）

　　S₂：作業2の作業可能時間 （h）

　　t： t_１＋ t_２　二作業のha当り所要作業時間 （h／ha）

　　t_１：作業1のha当り所要作業時間 （h／ha）

　　t_２：作業2のha当り所要作業時間 （h／ha）

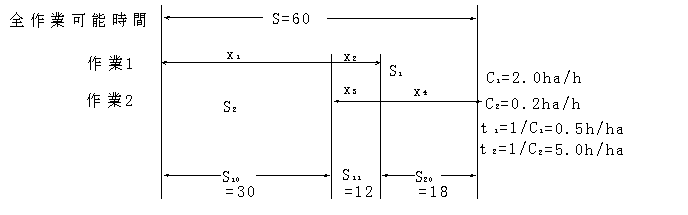
図3.8　二つの作業の作業期間が重複している場合

　　　t ＝ t_１＋ t_２ ＝ 0.5 + 5.0 ＝ 5.5（h）

　　　S ＝ 60, 　S_１= 42，S_２= 30から

　　　　　　　　　　 ＝min（10.9　84.0　6.0）

　　　　　　　　　　 ＝6.0（ha）　　　　　　　　　 eq. 3.3

　これは，作業２がこの組作業の複合負担面積を規制していることも示し，作業２の能力を大きくすることによって組作業の能力を増加することができる．

　組作業の数が増加し，作業可能期間や作業条件が複雑になると上記の手段では複合負担面積の算出が困難になる．そのような場合には，線形計画法を導入すると統一的な手法で算出できる．

　上記の事例を，線形計画法を用いて解く場合は，拘束条件式として，

　　　x_１≦S₁₀　　　　　　　　　　　　　　　　　　　eq. 3.4

　　　x_２+x_３≦S₁₁　　　　　　　　　　　　　　　　　 eq. 3.5

　　　x_４≦S₂₀　　　　　　　　　　　　　　　　　　　 eq. 3.6

　　　　　　　　　　　　　　　　　　　eq. 3.7

のもとで，目的関数

　　　　　　　　　　　　　　　　　　　　　　　eq. 3.8

を最大にすればよい．

　ここで，x_１，x_２は作業１のS₁₀，S₁₁期間の作業時間，x_３，x_４は作業２のS₁₁，S₂₀期間の作業時間であり，（3.7）式は，作業１の作業面積A_１=（x_１+x_２） ／t_１と作業２の作業面積A_２=（x_３+x_４）／t_２を等しくすることを意味している．

　（3.4）〜（3.8）式の制約条件式は,スラック変数x_５〜 x_８を用いるとつぎのような等式に書き変えられ，目的関数zを最小にする線形計画法の問題になる．ただし，Mは十分大きい正の数である．

　　x_１　　　　　　　+x_５　　　　　　　　　　　=30

　　x_２　　　　＋x_３　　　　+x_６　　　　　　　 =12

　　　　　　　　　　　　x_４　　　+x_７　　　　 =18

　　x_１+ x_２−0.1 x_３−0.1 x_４　　　　　 + x_８ 　 = 0

　z =−x_３−x_４+M * x₈を最小にする．

〔解〕　第２作業の所要時間ｚ＝−x_３−x_４＝−30,　すなわち，負担面積Ｈ＝−ｚ／t₂＝6.0（ha），したがって，第１作業の所要時間x_１+ x_２は，（x_３＋x_４）*t₁／t₂＝3.0（ha）である．

●ソフトウェア　作業日程計画プログラム　fw_sch80.exe

次へ