検索しやすいデータ構造というものは、今までにいくつも提案されています。二分探索木もそうですし、二分探索ができることからソートされた配列もそうです。今回はこの話をもうちょっと進めてみましょう。
では、今回の要点です。
では、いってみましょう。
突然ですが、あなたはとある学校の生徒になったとします。そして、あなたは友達の酒井君から、新谷君にあるものを渡して欲しいと頼まれたとします(これらは便宜上適当に付けた名前です)。しかし、新谷君は酒井君の友達ではあるのですが、あなたとは面識はありません。さて、あなたはどうしますか?
面倒だから他の人に任せる? そういうことを言っちゃダメです。それでは話が進みません。先ず多分、酒井君に新谷君がどのクラスの人かを聞くと思います。1年1組からしらみつぶしに探すようなことはしないと思います。なぜなら、クラスを聞いた方が断然速く見つかるからです。
このように、データを分類しておくと速く検索することができるのです。このことを利用したデータの管理・検索法をハッシュ法と呼びます。
ハッシュ法ではデータをハッシュ関数というものを使って分類します。この関数は特別な関数というわけではなく、あるデータを入れるとある一意に対応する値を返すだけの単純な関数です。返す値がある範囲にできるだけ一様に分布するようになっていれば、どんな関数でも構いません。そして、ハッシュ関数の返す値をハッシュ値と呼びます。
 |
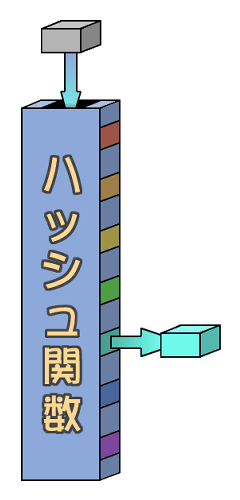
| 図.1 ハッシュ関数 |
|---|
例えば、左の図を見て下さい。上の灰色のデータをハッシュ関数に入れます。すると、赤色から紫色の値を返します。ここでは水色の値を返してきましたが、データによって赤色から紫色の7種類の値のどれかを返します。もちろん、データが同じ時は同じ色を返します。
そして、上の例では酒井君がハッシュ関数の代わりになっています。酒井君(ハッシュ関数)に新谷君(データ)のクラス(ハッシュ値)を聞いていますね。
あとは、このハッシュ値を使ってデータを分類すればいいだけです。次の図を見て下さい。
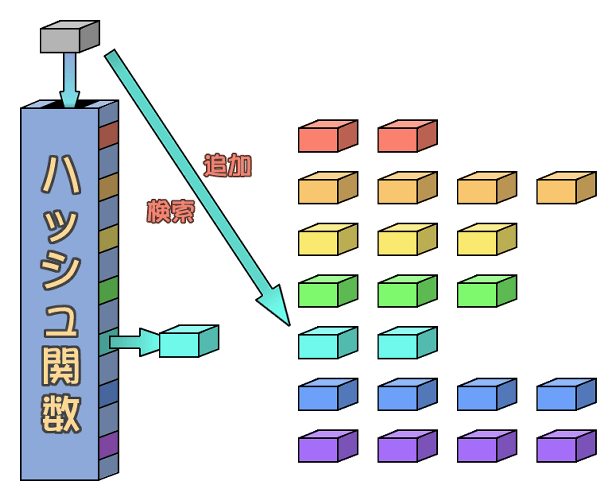 |
| 図.2 ハッシュ表 |
|---|
図の右半分は、ハッシュ値毎に分類されたデータです。赤色のデータは赤色のハッシュ値を返すデータです。他も同じようになっています。
さっき入れた灰色のデータは水色のハッシュ値に対応していました。なので、追加するときは水色のデータを集めたところに追加し、検索するときも水色のデータを集めたところを検索すればいいわけです。これがハッシュ法です。
最初の例では、新谷君(データ)を捜すには教えてもらったクラス(ハッシュ値)に行けばいいわけですね。あとは、このクラス内で新谷君(データ)を捜せばいいだけです。
では、実際問題の話をします。
先ず、ハッシュ関数をどういったものにするかです。ハッシュ値を求めるのに時間がかかるようではハッシュ法を使う意味がありません。なので、ハッシュ関数はそれなりに簡単な処理にする必要があります。
「これが一番いい!」というものは、扱うデータの傾向によって多少変わってきます。どんなデータでもなるべく一様になるようなハッシュ関数を研究してみるのもいいかもしれません。しかし、ここではそういう難しいところまでは踏み込みません。簡単なものを紹介するに止めておきます。
例えば、割り算の余りなどが便利です。特に、素数で割った余りがいいですね。偶数の多いデータなど、多少偏りがあっても対処できます。文字列では、最初と最後と真ん中の文字コードの合計を素数で割った余りなどにするといいでしょう。
次に、ハッシュ値に対応するデータをどう保存するかです。先ずはハッシュ値をインデックスとする配列を使うのはいいとして、その先のデータはどうしたらいいのでしょうか? 何の配列にすればいいのでしょうか? この中での検索時間が遅ければ、これまたハッシュ法を使っても大した効果は得られません。
これは簡単で、二分探索木やソートされた配列など、検索しやすいデータ構造を使えばいいだけです。先ずはハッシュ法で大雑把に分類して、その後に細かい検索をしていくわけです。
ハッシュ法を二重に使えばどうか、という話ですが、それはハッシュ値の範囲を広げることと同じです。ということで、ハッシュ法は一段階で構いません。また、データとハッシュ値とは一対一に対応しないので(ハッシュ値からデータが一意に定まらない)、最終的にはハッシュ法以外の検索が必要になります。
では、実際にプログラムを組んでみましょう。やたらと長いので別ページに載せておきます。
ハッシュ法は連想配列のように、種類が多く、バラバラな値とデータを結びつけるのに役に立ちます。この操作をマッピングとも呼びます。
では、今回の要点を振り返ってみましょう。
検索しやすいデータ構造にはまだデータベースに便利なB木などがあるのですが、それは各自で調べてみて下さい。
次回も検索をやりますが、検索しやすいデータ構造とは関係なくなります。それでは、次回まで。
Last update was done on 2001.2.13
この講座の著作権はロベールが保有しています