

| バリキャップ (varactor) のカーブフィッティング |
|
| ● |
LTC\SwCADIII\examples\Educational に
Fc.asc という
例があります。 これは capometer という SUBCKT を使ってバリキャップの静電容量と
バイアス電圧の関係を調べています。 英語では varactor が一般的のようです
が、varicap なる語もあって Web 検索で結構見つかります。 可変容量ダイオード DX を CR 直列回路に置き換えて試すと、capometer 測定の容量値は ともかく直列抵抗値は信用できません。 さらに直列抵抗が小さい場合でも容量が 5pF くらい になると、測定誤差が +10% にもなります。 Capometer の中身を調べようと一度は考えたのですが進んでいません。 ほか にも遅い、値が読みにくい、表示がきたない、などと文句を言いたくなります。 実は最初、{Cjo} / (1 + V(bias)/{Vj})**{m} 式を使い、データシートから 集めた値から Vj と m を決定し、.model としてシミュレートしてみた のです。 しかし capometer で測定した容量値は式と全然一致しませんでした。 Fc.asc 中の B1 式の max() を除いた部分はバリキャップの静電容量とバイアス電圧の 関係を表す数式です。 {Cjo} / (1 + V(bias)/{Vj})**{m} B2 の式は、順方向バイアス時のキャパシタンス減少係数 Fc (coeff. for forward-bias depletion capacitance formula) を考慮したもので、順バイアス電圧領域の話になります。 ({Cjo} / (1 - {Fc})**{1+m}) * ({1 - Fc*(1+m)} - {m/Vj}*V(bias)) そこで、別の測定回路を組んでみました。 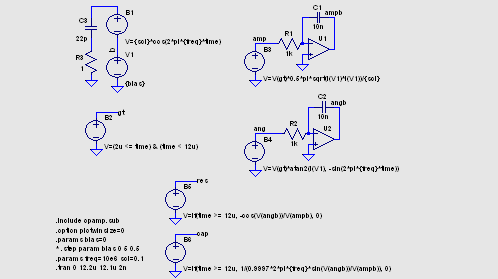 測定周波数は 10MHz です。 開始から 12.1us 後の V(cap), V(res) を読み出すと、接合 容量・直列抵抗が直読できます。 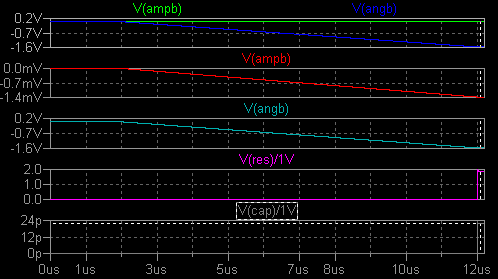 直列抵抗の値は、やはり正確に求めるのは困難でした。 50Ω を超えるとそれらしい値が 求まりますが、そんなバリキャップは使いたくありませんよね。 B6 の計算式中の係数 0.9997 は、理論でなく実地に試して容量値がほぼ正しくなるように 選んだ値で、直列抵抗 1Ωの場合を基準にしています。 直列抵抗値はあきらめて、{bias} を変えて MV2201 の容量値をプロットしてみま した。 Plot Settings の Mark Data Points 機能を ON にしています。 これなら マウスカーソルの位置を読み取る機能を利用して容量値が読みとれま すし、C1V/C4V などの計算表示もできます。(あまり見栄えはよくありませんが。 次項参照。) 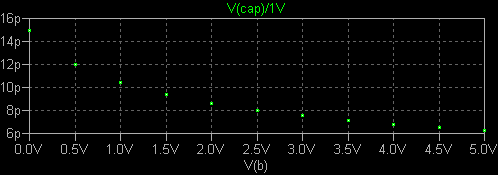 varact1.asc varact1.plt |
| ● |
Cjo / (1 + Vbias/Vj)**m 式には単純な比例定数 Cjo
のほかに 2 つの係数があります。 したがって
3点の電圧における2つの容量比を定めれば、Vj と M が決まります。 例えば逆バイアス電圧 1, 2, 4V における容量値を c1v, c2v, c4v として、これらが わかっているとすると、 c1v/c2v = (Cjo/(1 + 1/Vj)**m) / (Cjo/(1 + 2/Vj)**m) = ((1 + 2/Vj) / (1 + 1/Vj))**m c1v/c4v = ((1 + 4/Vj) / (1 + 1/Vj))**m ln(c1v/c2v) = m * ln((1 + 2/Vj) / (1 + 1/Vj)) ln(c1v/c4v) = m * ln((1 + 4/Vj) / (1 + 1/Vj)) ln(c1v/c2v) / ln(c1v/c4v) = ln((Vj+2)/(Vj+1)) / ln((Vj+4)/(Vj+1)) ここで Vj が求まります。 そのあと m = ln(c1v/c2v) / ln((Vj+2)/(Vj+1)) 式で m が 求まります。 c1v 等の具体的な容量値から Cjo が決定できます。 具体例を示します。 1SV331 のデータシートから容量値を読み取りました。 C1V/C4V の 標準値は 3.75 とされていますが、グラフから読み取った値は 3.664 程度 でした。 グラフの形がいかにもゆがんでいるのですが、そのまま進みます。 1V 17.89p 2V 10p 4V 4.882p 6V 3.813p ln(c1v/c2v) / ln(c1v/c4v) = ln(17.89/10) / ln(17.89/4.882) = 0.4479 ln((Vj+2)/(Vj+1)) / ln((Vj+4)/(Vj+1)) = 0.4479 → Vj=0.862 m = ln(c1v/c2v) / ln((Vj+2)/(Vj+1)) = ln(17.89/10) / ln((0.862+2)/(0.862+1)) → m=1.353 Cjo = 17.89p * (1+1/Vj)**m = 50.72p 検算: c1v=Cjo/(1+1/Vj)**m = 17.89p c2v=Cjo/(1+2/Vj)**m = 10.00p c4v=Cjo/(1+4/Vj)**m = 4.882p c1v/c2v = 1.789 c1v/c4v = 3.664 このパラメーターでシミュレートしました。 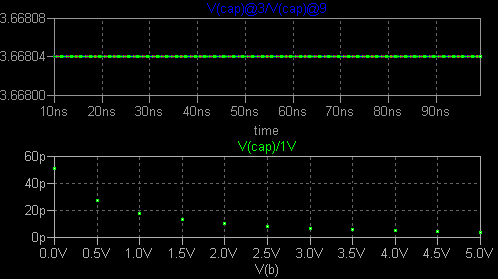 C1V すなわち V(cap)@3/1V は 17.91p と読み出せます。c1v/c4v すなわち V(cap)@3/V(cap)@9 は グラフから 3.668 と読み取れます。 3桁程度の正確さで確認測定ができました。 varact3.asc varact3.plt (シミュレーション終了後、目盛りの範囲や刻みを手動調整する必要があります。) Vj と M の働きをまとめます。 ・ M 増加 → 容量比が大きくなる。 ・ Vj 増加 → グラフの横軸を拡大したような効果がある。 容量比は少し減少する。 Vj を小さくすると逆バイアス電圧が大きな領域での容量変化が少なくなる。 1SV331 のデータシートは http://www.semicon.toshiba.co.jp/td/ja/Diode/Variable_Capacitance_Diode/20020111_1SV331_datasheet.pdf にあります。 1pF に近い小さな容量や直列インダクタンスを気にするのなら、 http://www.eetasia.com/ARTICLES/2002SEP/A/2002SEP20_BD_RFD_AN.PDF で紹介されている通り、Cv = Cjo/(1 + Vr/Vj)**m + Cp 式を使い、Rs, Ls も しっかり記述したほうが正確だと思います。 係数 Fc のことを調べているうちに次のページを見つけま した。 http://www.daryan.de/admin/download/file_104.pdf ダイオードに限らず、各種素子のモデルについて解説されています。 (怪しい URL ですね。) |
| ● |
過渡解析でなく、AC 解析でバリキャップの振る舞いを調べました。 まずは
CR 直列回路で試します。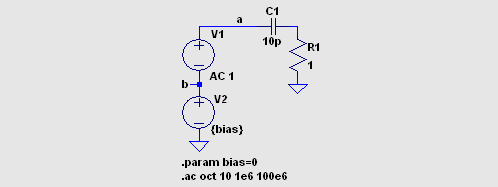 グラフは上から順に回路電流、キャパシタンス、直列抵抗値、インピーダンスと位相角 (360 分度)、位相角のみ、Q の値です。 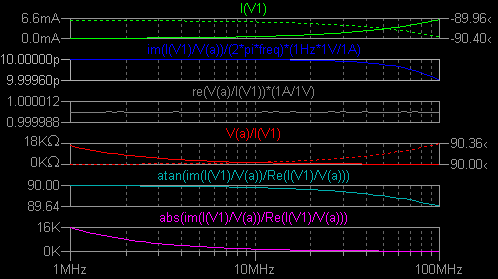 nl_cap1.asc nl_cap1.plt 測定値の確からしさ (測定周波数 10MHz)
赤字の部分は全く信頼できない値です。 しかし直列抵抗の値はとても正確です。 1SV331 をシミュレーション測定しました。 .model に Rs=0.45 を追加してあります。  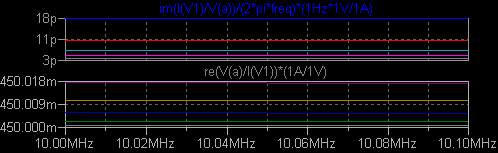 残念ながら、グラフの横軸を V(b) には変えられませんでした。 しかしグラフの ウィンドウを選択した状態で File → Export し、Format を Cartesian: re,im と指定 して、結果をテキストファイルに書き出すことができます。 ちょっとわかりづらいの ですが、ちゃんと報告されています。 Freq. im(I(V1)/V(a))/(2*pi*freq)*(1Hz*1V/1A) re(V(a)/I(V1))*(1A/1V) Step Information: Bias=1 (Run: 1/5) 1.00000e+007 -1.78911e-011, 0.00000e+000 -4.50001e-001, 0.00000e+000 1.01000e+007 -1.78911e-011, 0.00000e+000 -4.50001e-001, 0.00000e+000 Step Information: Bias=2 (Run: 2/5) 1.00000e+007 -1.00011e-011, 0.00000e+000 -4.50003e-001, 0.00000e+000 1.01000e+007 -1.00011e-011, 0.00000e+000 -4.50002e-001, 0.00000e+000 Step Information: Bias=3 (Run: 3/5) 1.00000e+007 -6.66751e-012, 0.00000e+000 -4.50006e-001, 0.00000e+000 1.01000e+007 -6.66751e-012, 0.00000e+000 -4.50006e-001, 0.00000e+000 Step Information: Bias=4 (Run: 4/5) 1.00000e+007 -4.88270e-012, 0.00000e+000 -4.50011e-001, 0.00000e+000 1.01000e+007 -4.88270e-012, 0.00000e+000 -4.50010e-001, 0.00000e+000 Step Information: Bias=5 (Run: 5/5) 1.00000e+007 -3.79101e-012, 0.00000e+000 -4.50018e-001, 0.00000e+000 1.01000e+007 -3.79101e-012, 0.00000e+000 -4.50017e-001, 0.00000e+000 nl_cap2.asc nl_cap2.plt |
| ● |
コンデンサーに流れる電流は両端電圧の時間微分に比例
する、という根本的な性質を思い出して、次の方法で容量値をシミュレーション測定して
みました。 これは直列抵抗は小さくて無視できる、という前提での話になります。 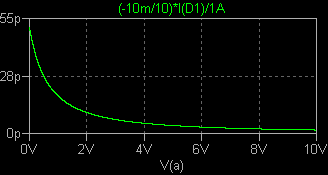 グラフを拡大しカーソルを注意深く設定して読み取りました。(これがちょっと やっかい。) かなり正確と言えます。 c1v = 17.8936p c2v = 10.0046p c4v = 4.8882p c6v = 3.07089p c1v/c4v = 3.66057 nl_cap3.asc nl_cap3.plt |
| もどる |
| |