

| FFT を利用した歪の評価 |
|
| ・ | 増幅器の
歪み率を調べようとするとき、まずは信号源を作ってそれを増幅し、入出力信
号のようすを比較します。 いい加減に FFT を行うと正弦波信号源の高調波が大きく見えてしまってどうしようも ありません。 普通に電圧比 -30dB くらいにも見えてしまいます。 せいぜい こんなものなのでしょうか。 いや違います。 設定をちゃんとすればいいのです。 ここ では可聴周波数帯域を例にとりますが、考え方はどの周波数帯でも同じです。 FFT の「データ点数」などと呼び習わしているもの (LTSpice で は Number of data point samples in time)、これが周波数領域の分解能を 決定します。 着目する周波数の上限と下限の比と言ってもいいでしょう。 10Hz 〜 320kHz 程度 の範囲を考えるなら、周波数の比は 32000 だから 32768 点の FFT で間に合いそうですが、折り返し 雑音のために結果の半分は利用できないので、65536 点の FFT が必要です。 次に最低周波数ですが、これはどのくらいの時間ぶんのデータを集めたかによって決まり ます。 計算は単純で、最低周波数 = 1/データ収集時間です。 最後にシミュレーションの 最大時間刻み Maximum Timestep を決定します。 これはデータ収集時間の 1/65536 に設定します。 1kHz の正弦波信号を JFET で増幅してみました。 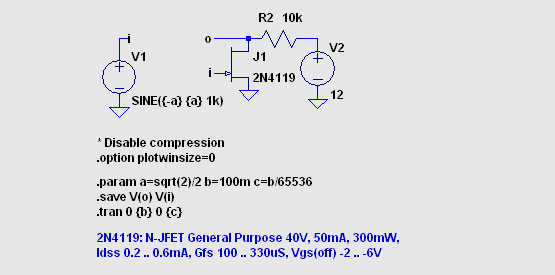 「.option plotwinsize=0」指定によってデータ圧縮を禁止しています。 変数 a は入力信号の振幅です。 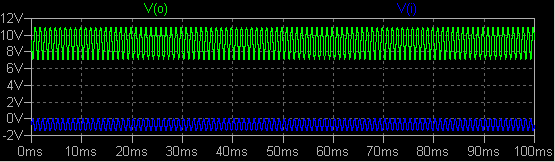 過渡応答グラフを右クリックして FFT を選択します。 V(o) および V(i) を指定 し、Number of data point samples in time は 65536 にします。 スムーシング (Binominal Smoothing done before FFT and windowing) の設定は、比較的 低い周波数に着目しているので大きな影響はありません。 今回は 3 に設定しました。 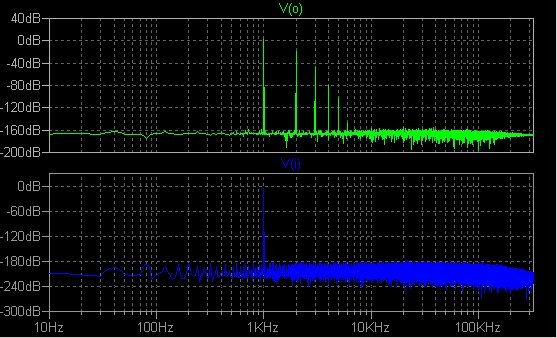 このように信号源 V(i) の雑音成分は -180dB 程度以下に抑えられ、増幅器の歪み率を充分に評価でき ます。 ソース 信号周波数をデータ収集時間に対して半端な周波数にするとスペクトラムが広がって見えますが、 これは bin splatter とも呼ばれる DFT (Discrete Fourier Transformation) の原理的な性質です。 |
| ・ |
前項では FFT データ点数を 65536 にしましたが、いつもこんなに広い
周波数帯域に注目するわけではないでしょう。 デフォルトの 16384 点 FFT の場合はどのような設定が
できるのか、表にまとめてみました。
時間の刻み time step は .param で変数の値を設定し、それを .tran に記述したほうが正確です。 「.option plotwinsize=0」をお忘れなく。 注目する信号波は最低周波数の少なくとも 50 倍 に選ぶのがよいでしょう。 実のところ、これは見栄えの問題なのですが。 |
| ・ |
これまでの例は DC 動作点がすぐに
安定する回路なので簡単でしたが、実際の回路はそうもいきません。 なか
なか DC 動作点が定まらない回路の場合はどうしたらいいでしょうか。 DC 動作点の設定はけっこうな大きな問題で、関連したドットコマンドがいくつかあります。 .IC -- Set initial conditions .NODESET -- Supply hints for initial DC solution .SAVEBIAS -- Save operating point to disk .LOADBIAS -- Load a previously solved DC solution .tran コマンドには UIC, startup などのオプション (modifiers) があります。 まずは例を一つ。 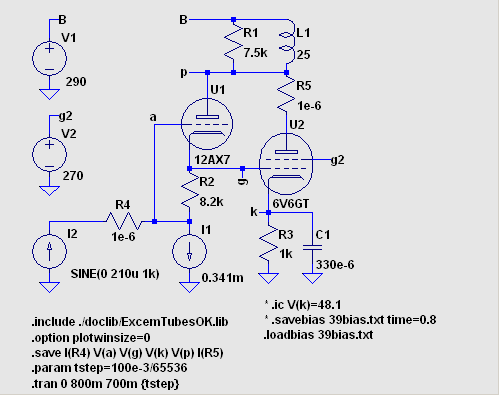 当初 1.2s くらい経過しないと DC 動作点が安定しませんでした。 そこで .ic V(k)=48.1 を 指定すると、0.8s 程度で安定するようになりました。 その後 .savebias と .loadbias を 試したのですが、劇的な改善には至っていません。 データ圧縮を禁止しているので、必要なデータのみを記録するように .save を使用してい ます。 R4, R5 は .save で回路電流値を指定するためのダミー抵抗です。 (ノード電流を知りたい場合は電圧 0V の電圧源を利用するのがよい方法です。 後述。) おことわり 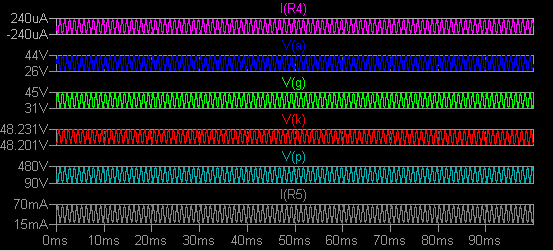 FFT データ点数は 65536 と指定します。 I(R4) が入力信号、V(p) が出力信号です。 これ↓なら歪み率の評価に自信が持てます。 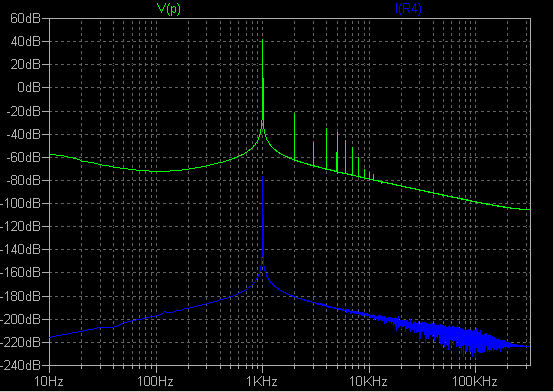 dstr2.asc ExcemTubesOk.lib 39bias.txt dstr2.plt (ExcemTubesOk.lib は http://groups.yahoo.com/group/LTspice/ の files/Lib/cmp/ から 入手しました。) |
| ・ |
この場合、なぜ信号源の 2kHz 付近のノイズレベルが -100dB
程度になってしまうのか、
原因を追求してみました。 実は LTSpice の演算精度 (分解能・桁数) は 16 桁程度
です。 これが問題ではないだろうか? FFT の原理からいって、測定時刻が平行移動
するだけならパワースペクトラムの計算結果は変わらないはずです。 このような考え方から、.tran コマンドを .tran 0 800.1m 700m {tstep} に変更しました。 さらに FFT 実行時に、 Use Extent of Simulation Data ではなく、 Use current zoom Extent でもなくて、 Specify a time range これを選択し、 End Time を 100ms と指定し直します。 結果は: 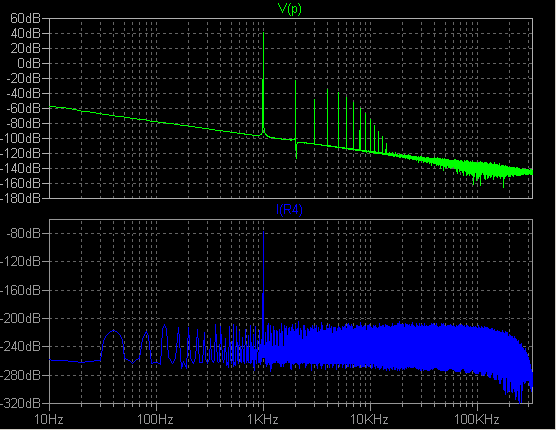 入力信号 I(R4) のノイズフロアレベルの相対値は -130dB ほどになりました。 解説すると、浮動小数点演算の丸め誤差のためにデータが1つか2つ足りなかった のを適当に処理されていた、ということでしょうね。 あらかじめ予備のデータを取得 しておけば、けっこうまともに動いてくれました。 感謝です! この「適当に処理」とは、時間軸方向の伸縮を行って、さらに補間法を使ったのではないか と思います。 なんとなく信号のスペクトラムの幅が広がっているように見えるので。 |
| ・ | 前記 V(p) のグラフについて、右下がり直線状の ノイズフロアが見えます。 これの傾きは -20dB/decade ですから、何かのインパルス 応答でしょう。 まだ DC 動作点が安定していないと考えられます。 |
| ・ |
サンプリング周期 (時間の刻み) を 1/2 にして、同じことをしてみました。 .param tstep=100e-3/(65536*2) .tran 0 800.1m 700m {tstep} FFT 実行時にデータ区間を 100ms に指定し直します FFT 点数が 65536 なら大きな変化はありません。 データを1つ飛ばしに使うようなもの です。 スムーシングに関しては、間のデータも使うのではないかと思います。 FFT 点数を 131072 に設定する意味はあります。 このときの上限周波数は 327.68kHz の 2 倍 である 655.36kHz になります。 次にデータ収集期間を 200ms にします。 .param tstep=100e-3/65536 .tran 0 900.1m 700m {tstep} FFT 実行時にデータ区間を指定し直します 65536 点の FFT であっても、データ区間を 100ms と指定した場合と 200ms とした 場合では差があります。 統計で言うサンプル数を増やすことに相当し、グラフ上のスペクトラム が鋭く、ノイズが減ったように見えます。 |
| ・ |
スムーシング、
Binominal Smoothing done before FFT and windowing の binominal とは2項分布の
ことで、ある点のデータを前後のデータとの重みつき平均によって求めます。 現実の
測定データであってノイズが含まれている場合はスムーシングも有効でしょうが、
シミュレーション結果のデータに対する効果は疑問です。 特に増幅器の歪の性質を
調べようとする場合は、無関心でいいでしょう。 Windowing Function つまり FFT の窓関数ですが、これも現実の測定データであって 信号周期が不明な場合に使用すると有効な場合があります。 シミュレーションなら 自励振動などがこの例にあてはまります。 しかし、どの窓関数にも一長一短があって、 万能というわけにはいきません。 皮肉にも窓関数の種類がたくさんあるのが その証拠です。 現実にはいくつかの窓関数を試してみて、よさそうなものを 選択する方法がよいでしょう。 なお窓関数を使わない場合に周波数分解能が 最高になります。 スムーシングや窓関数の設定を変更するとデータ区間の長さ指定 (Start Time, End Time) が リセットされてしまいます。 OK ボタンを押す前に確認したほうがいいでしょう。 私は このせいで首をひねったことがありました。 |
| ・ |
ドットコマンドに .four というのがあって、
これと .step param を利用して FFT 結果をまとめることができます。 しかし
今回のように DC 動作点が安定するまで待ってから FFT を行おうとすると、
データ不足の問題が生じるため、一筋縄ではいきません。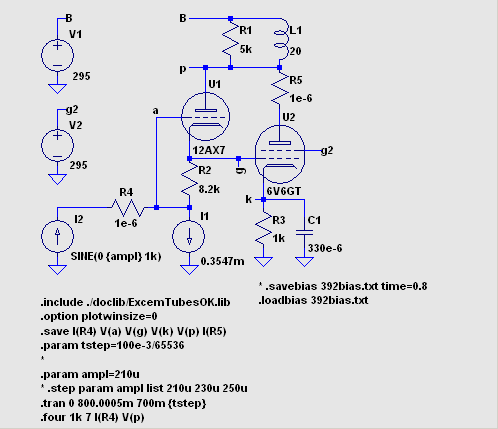 この回路で 700ms ほど待てば DC 動作点が安定することがわかりました。 まず は .tran 0 800m 700m {tstep} を実行して FFT を選択してみます。 する と End Time が 99.9995ms になっています。 浮動小数点 演算の丸め誤差のために 0.0005ms 分のデータが不足しているわけです。 そこで .tran コマンドを .tran 0 800.0005m 700m {tstep} に変更します。 FFT の グラフを見て問題がないことが確認できたら、.param ampl= を .step param ampl list .. に 変更します。 ".four 1k 7 I(R4) V(p)" は基本波 1kHz とし、その第 7 次 高調波までの振幅と位相を *.log ファイルに書き出します。 お茶でも 飲みながら結果が出るのを待ちましょう。 dstr3.asc 392bias.txt dstr3.log |
| 注: MS Internet Explorer を
お使いで、dstr3.log の内容が崩れて見える皆様へ。 表示 → 文字エンコードで、
自動選択を指定してみて下さい。 次項の dstr4.log も同様です |
| ・ | その後、ノード電流の測定はダミー抵抗でなく、0V の
電圧源を利用するほうが正確であることがわかりました。 また、
バイアス安定化回路を加えました。 C2 22pF は異常発振防止用
です。 2N5210 は Vceo 50V ですので、耐圧の余裕がやや不足です。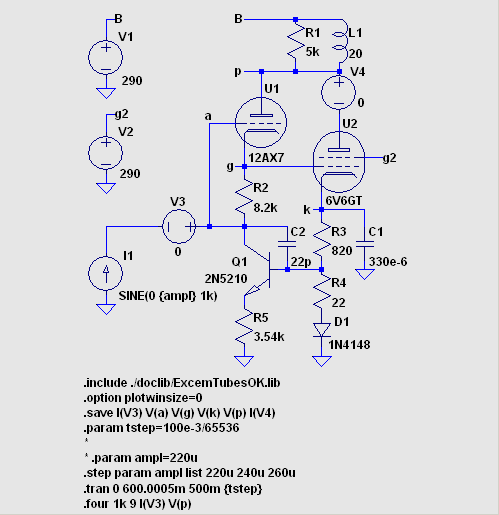 dstr4.asc dstr4.log 入力信号の高調波歪は -170 〜 -180 dB 程度であることがわかります。 入力 (peak to zero) と 出力の全高調波歪みの関係は次の通りとなりました。 220μA 0.305272% 240μA 0.361561% 260μA 0.558938% 高調波の次数ごとの歪み率、信号振幅との関係は dstr4.log を御覧下さい。 この回路のままで I1 の AC 振幅を指定すれば .ac 解析ができます。 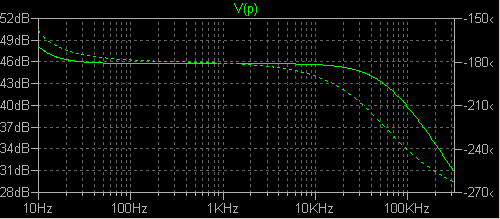 |
| もどる |
| |