ttl.png


 結果のプロットとグラフの座標軸
・ 各種解析結果のまとめ方 や、グラフの座標軸の変更について説明します。

Q1 とその周辺 CR からなる 1 Tr の増幅器をシミュレーション対象に します。 測定周波数は 1MHz で、入力信号振幅を変えたときの振る舞いに注目します。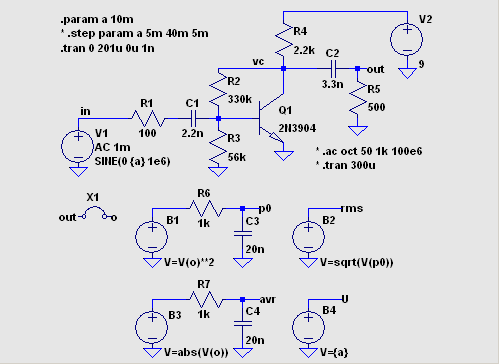

1.png

RMS 値と絶対値の平均値の測定回路が作り込んであります。 B1, B2 は X1 ジャンパーの 左側のラベルの信号の RMS 値を素朴な方法で電圧値に変換します。 B3 は 同様に平均値を電圧値に変換します。 B4 電圧源はあとで説明します。

過渡解析によると開始後 200us ほど経過すれば各部が安定することがわかりました。
(このような作業を何回も行うつもりなら、データを別のプログラムによって 処理させるのがはるかに能率的ですが、その方法は別の機会にゆずります。)

下記のようなグラフのトレース名を CTRL キーを押しながら左クリックすると平均値 と RMS 値をダイアログボックスに表示する機能はありますが、その値を取り込んで プロットすることはできません。 数値をコピーペーストすることはできますが。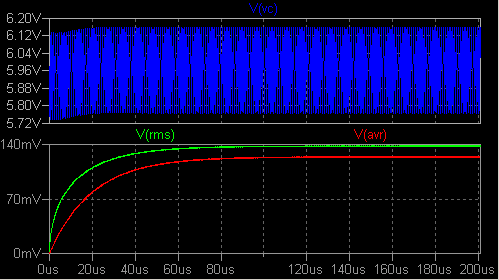

2.png


次に、変数 a (入力信号振幅) を .step 5m 40m 5m とステップ変化させます。 .tran は .tran 0 201u 200u 1n に 変更します。 201μs と 200μs の差の 1μs は測定周波数の一周期に選びました。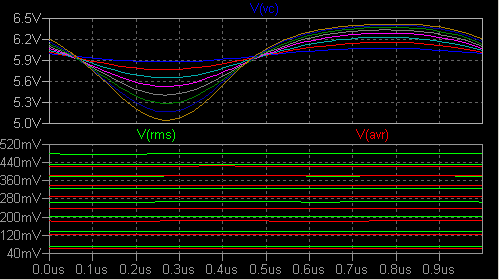

3.png

V(rms) ペーンを右クリックして Sync Horiz Axes の チェックを反転させます。 横軸目盛りの位置にマウスカーソルを移動させると カーソルが定規の形になります。 ここで左クリックして Quantity Plotted を V(U) に 設定します。 さらに V(rms) ペーンを右クリックして Mark Data Points を設定します。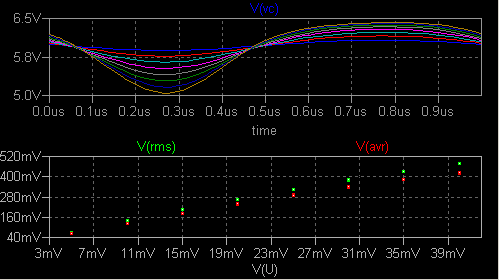

4.png

Plot Settings → Notes & Annotations によって、手動で折れ線やマークを 書き加えることもできます。

V(rms) のプロットを折れ線で結んでみると、けっこう直線的に見え ます。 しかし V(vc) の時間軸グラフを見ると、振幅が大きくなるにしたがって 波形がかなり歪んでいます。

そこでペーンを一つ追加し、V(vc) のグラフを最上段に移動させ、Add Trace で 中央のペーンに V(rms)/V(U) をプロットさせます。 横軸は V(U) に して Mark Data Points を設定します。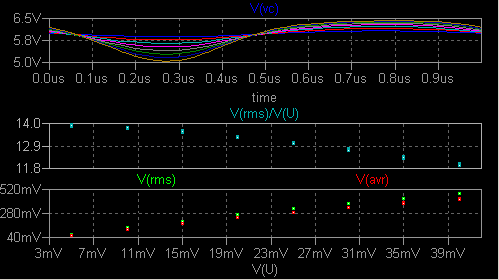

5.png


入力振幅の増大に伴って、利得が着実に低下していることがわかり ます。 なお V(U) は peak to zero の値であるのに対して V(rms) は 名前の通り RMS 値であることに注意して下さい。

横軸の Quantity Plotted を V(U)/1mV に変えると、それなりにグラフの目盛り ラベルが変わるのは立派です。 V, A, ohm, W, s などは認知してくれます。

　axis2.asc 　axis2.plt

この方法は、何と言っても 1kΩ と 20n の積分回路の応答が安定するのを待つのに時間がかかります。


・
 前項の最初の過渡解析 グラフ (.param a 10m, .tran 0 201u 0u 1n) を見ると、V(vc) は 50μs も経てば 安定しているようですから、この辺の交流 RMS 値を取り込む方法はないものかと考えて みました。 積分器と測定 (積分) する／しないを示すデジタル信号を使います。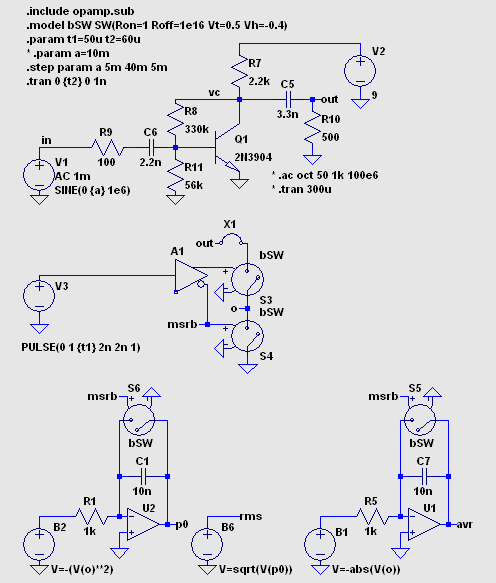

6.png

V3 出力が 1V のとき、測定を行います。 peak to peak 測定回路をおまけでつけました。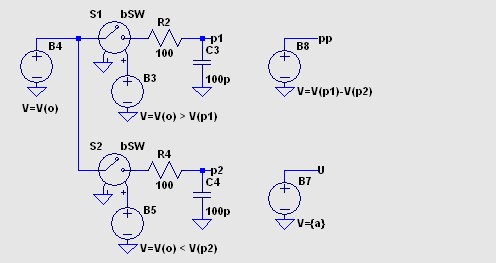

7.png

ここで .tran 0 {t2} 0 1n を実行すると次のように見えます。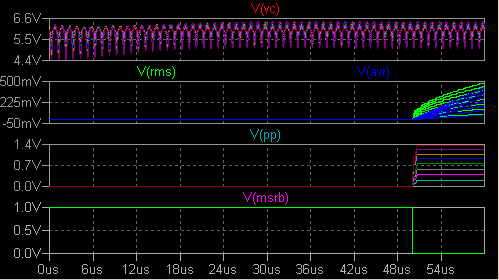

8.png

V(msrb) が「測定しろ」という信号の論理反転です。 {t2-t1} は 10μs です から、1MHz 信号の 10 波分を積分することになります。 次にコマンド を .tran 0 {t2} {t1} 1n に変えて実行します。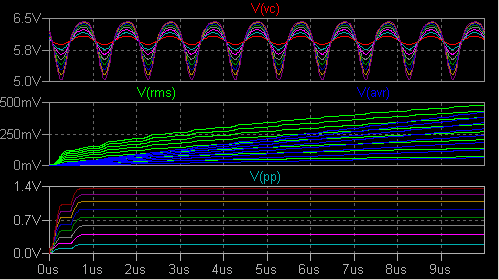

9.png

V(vc) の波形はなかなかきれいですが目的には合いません。 コマンド を .tran 0 {t2} {t2-100n} 1n に変えます。 グラフの横軸は V(U)/1V に して Mark Data Points を設定します。 V(rms)/V(U) のペーンを追加しました。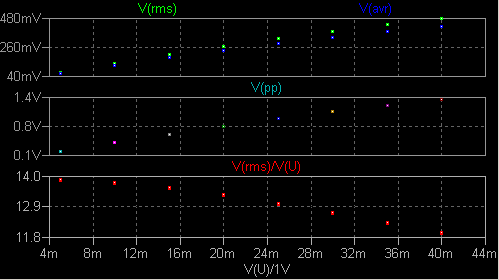

10.png

V(rms)/V(U) をプロットした点の位置も、前項の場合と見た目にはそれほど変わりま せん。 こちらには積分リップルがありませんので表示区間を 100ns に 縮めていますから、点の位置がしっかりと定まります。

これでシミュレーションに必要な時間がだいぶ短縮できました。

　axis3.asc


・
 その後、測定のための回路を簡略化しま した。 平均値測定回路は除外し、被測定回路も少し変更してあります。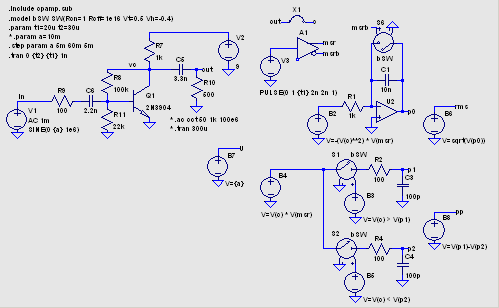

11.png

この例の場合、入力信号によって Q1 の動作点が変化するので、それが安定するまで 待ってから測定を開始する必要があります。 やたらに大きな信号を加えなければ 20μs 程度 で動作点が安定することがわかりました。

表示は横軸を V(U)/1V にとり、Mark Data Points を設定してあります。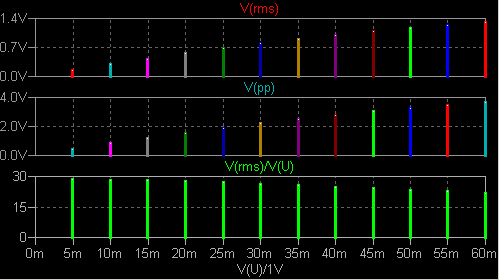

12.png

このように、棒グラフとして見えます。

測定部の積分コンデンサーをリセットするスイッチは不要にも思えますが、積分値を 途中でリセットできるように残してあります。 とは言っても p-p 測定回路に リセット機能はないので、ちぐはぐですが。

　axis4.asc 　axis4.plt


回路の動作が安定したところで、一周期 (もしくはその整数倍) の 期間の平均値を測定する、という処理は一般的なものです。 LTSpice/SwitcherCAD III に は Efficiency Report 機能があって、.tran の特別な オプション steady と共に使います。 しかしこれは LTC 製品のマクロモデルを 使っているときのみ利用できます。 何をもって steady state と判断する のか、どこからどこまでの平均を求めるのか、自動判断はむづかしいでしょう。


後日、ある区間の信号を積分するなら .measure が使えることに気づきました。 結果は ErrorLog ファイルに出力されます。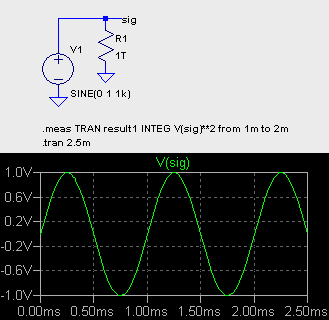

13.png
result1: INTEG(v(sig)**2)=0.000497018 FROM 0.001 TO 0.002

しかし結果が少し不正確です。 float(integrate(sin(x)**2, x, 0, 2*%PI) / (2*%pi)) は 0.5 です (数式処理プログラム MAXIMA での書式)。 LTspice に指定した 積分時間は 1ms ですから、0.0005 になってほしいのですが。

過渡解析の maxstep を指定し、かつ .options plotwinsize=0 を指定すると 正確な値が求まりました。 使い方を誤ると不正確な結果が得られると いう、悪い例になってしまいました。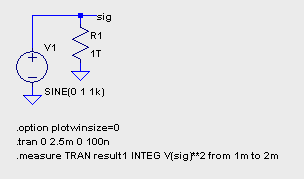

14.png
result1: INTEG(v(sig)**2)=0.0005 FROM 0.001 TO 0.002



もどる
Valid HTML 4.01!