1998.5.12
あなたは〈一筆書き(ひとふでがき)〉というのを知っていますか。知っている人は,知らない人にくわしく教えてあげましょう。また,書ける人は下に一筆書きで図を書いてみましょう。
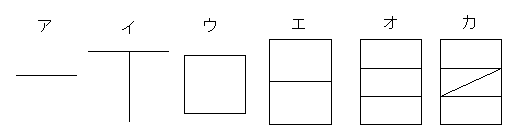
一度,書き始めたらペン先を紙から離さずに最後まで書く図形を一筆書きといいます。ただし,一度とおった線とは交わってもよいが,同じ線を二度となぞってはいけません。
次の図形は一筆書きで書けると思いますか。書けるか書けないか見当をつけてから,一筆書きを書いてみましょう。
(書くときは,書き始めと書き終わりの点に・印をつけて書き方が分かりやすいようにしておきましょう)

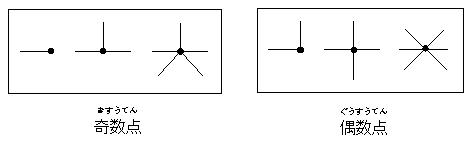
一筆書きの図形の頂点(ちょうてん)や線の交点に目をつけてください。すると,一つの点から出ている線が奇数個の場合と偶数個の場合があることがわかります。奇数個の線が出ている点を奇数点,偶数個の線が出ている点を偶数点とよぶことにします。
(2の倍数である整数…,0,2,4,6…を偶数,2の倍数でない整数…,1,3,5,7…を奇数という)
【作業】
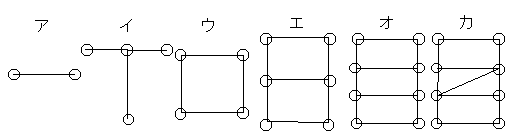
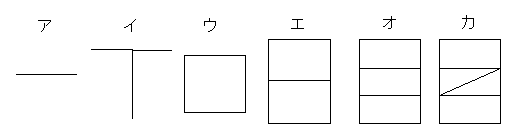
【問題1】の図形の奇数点と偶数点の数を数えてみましょう。○印の点に目をつけて数えよう。
|
ア |
イ |
ウ |
エ |
オ |
カ |
|
|
奇数点の数 |
||||||
|
偶数点の数 |
||||||
|
一筆書きは |
図形には,一筆書きで書けるものと,どんなに工夫しても書けないものがあります。
では,一筆書きで書けるか書けないか,書く前に図形を見分けるうまい方法はないでしょうか。すこし考えてみてください。もし,いい考えを思いついた人がいたら,みんなに説明してあげてください。
ある日,理香さんは図書室で,次のようなお話をみつけてきました。
…
今から270年ほど前のリトアニアにケーニヒスベルクという大きな町がありました。現在,この町はロシアの領土になっていますが,つぎの話はまだケーニヒスベルクがリトアニアのものだった時代の話である。
この町の真ん中には,今でもプレゴリヤ川という大きな川が流れているが,この川には七つの橋がかけられていた。が,あるとき,この町の人がこんなことをいいだした。
「この川にかかっている七つの橋をぜんぶわたって,もとのところに帰ってくることができるか。ただし,どこから出発してもよいが,同じ橋を2度わたってはいけない。」
というのである。
すると,
「これはおもしろい。これがわかれば,この町にはじめてきた人を案内するのに,とてもつごうがよいじゃないか。」
というので,この問題はたちまちひょうばんになって,たくさんの人が考え始めた。
ところが,どうしたことか,これがなかなかむずかしい。だれがやってもできないのだ。そうなるとまた,この問題はますます有名になって,しんけんにこの問題を考える人たちが出てきた。
ここで,あなたもこの問題を考えてみてください。七つの橋を2度とおらずにすべて通ることができると思いますか。
[予想]
ア.すべて通ることができる。 イ.そんなことはできない。
ところが,そこにたまたま,オイラーという有名な数学者がやってきた。
そこである人がオイラーにこのことを話すと,かれはあっけなく答えを出してしまった。
ところが,その答えがふるっている。
「そんなことは,どんなに頭をしぼってもできっこない。」
というのだ。
「なーんだ。オイラー先生もできないのか。」
と,みんなはほっとしたが,オイラーはいった。
「いや,これはだれがやったってできっこないのですよ。」
といいくわえた。つまり,この問題は,もともと答えのない問題だというのだ。そしてオイラーはそのわけをこう説明した。
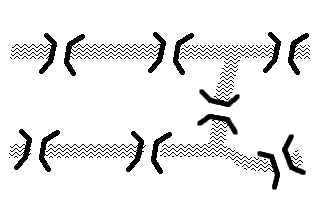
「まず,地図をかんたんにして通る道すじだけをかんたんに書いてみましょう。すると,こんな図が書けます。![]() 印をつけたところが橋です。問題はこれだけの道を同じところを二度通らずにぜんぶ歩けというわけですね。ところが,この図は,つづけざまに一本の線でつないで書くことができないのです。」
印をつけたところが橋です。問題はこれだけの道を同じところを二度通らずにぜんぶ歩けというわけですね。ところが,この図は,つづけざまに一本の線でつないで書くことができないのです。」
オイラーは,一言こういったあと,まだみんながうたがいぶかそうな顔をしているので,もっとくわしく説明をした。しかし,オイラーがどういう説明をしたか,くわしいことはわからない。
(板倉聖宣「一筆書きの数学」『数と図形の発明発見物語』国土社より)
…
「へー,できないってことを証明したのか。それにしても,いったいどんな説明をしたのだろう。」
と秀夫君が首をかしげながらいいました。
理香さんは,
「これって,つまり〈一筆書きでは,どんな図形が書けてどんな図形が書けないか〉ということよね。わたしも考えたのだけど,どうしてもこの図だと一筆書きで書けないわ。でも,なぜなのかわからないの。みんなも考えてみてよ。」
と,確かめるようにみんなにいいました。
工作君は,紙を持ち出していろんな一筆書きの図を書きながらぶつぶついいだしました。
「日の字形はかんたんに一筆書きが書けるのだけどなあ。」
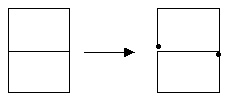
「でも,線を一つ加えただけの目の字形は,ぜったいに書けないや。この二つのちがいってなんだろう?」
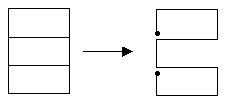
「どうしてこんなことになるのかな。」
ほかのみんなも紙に書きながら考え出しました。
ここで,みなさんも,もう一度どんな場合に一筆書きができたりできなかったりするか,考えてみましょう。
みんなの話をだまって聞きながら,いろんな一筆書きをためしていた恵美子さんがこんなことを思いつきました。
「ねぇ,なんだか分かったような気がするわ。奇数点の個数と偶数点の個数を比べてみるのよ。奇数点の個数が0とか2のときはできるけど,4個になるととたんに書けなくなるでしょ。でも,偶数点は同じ個数でも奇数点しだいで書けたり書けなかったりするじゃない。」
|
ア |
イ |
ウ |
エ |
オ |
カ |
|
|
奇数点の数 |
2 |
4 |
0 |
2 |
4 |
2 |
|
偶数点の数 |
0 |
0 |
4 |
4 |
4 |
6 |
|
一筆書きは |
○ |
× |
○ |
○ |
× |
○ |
秀夫君が「あっ」という小さな声を出してうなずきました。
「なるほど,書けるか書けないかは奇数点しだいっていうことか。」
理恵さんも明るい顔でいいました。
「奇数点が0個か2個だと一筆書きができるけど,それより多いと書けない,というのね。」
工作君は大きな声でいいました。
「そうだ,そうだ。ぼくもそう思っていたんだ。」
そのとき,理恵さんが自分にたずねるようにいいました。
「でも,不思議ね。なぜ,そんなことになるんでしょう。本当にどんな図形でも,そんなことがいえるのかしら。」
これには,秀夫君が答えました。
「それは,まず,一の字形を一筆書きすると考えたらどうだろう。書き始めと書き終わりは奇数点になって奇数点は2個になるね。書き始めと書き終わりは奇数点であっても一筆書きできるんだ。そして,奇数点が2個だとそのどちらかから必ず書き始めなくちゃならないんだ。つまり,奇数点があったら,それは書き始めか書き終わりでなくてはならないんだよ。
つぎに,Tの字形を一筆書きしようとすると奇数点が4個になって書けなくなるね。一筆書きの書き始めと書き終わりは合わせて二つしかないから,奇数点が2個より多いと書けっこないんだ。
それに,とちゅうで通る点というのは,入ってくる線と出ていく線がいるから偶数個の線が出ている偶数点でなければならない。Tの字形は真ん中が奇数点だからよけいに書けないよ。」
工作君も元気よくいいます。
「そうか,口の字形だと奇数点が0個で偶数点が4個。それで,偶数点ばかりだったら,どこからでも書けるというわけか。しかも,書き始めの出発点に必ずもどってくるね。」
話がどんどん進むので理香さんがあわててまとめました。
「待って待って,話をまとめてみるわね。つまり
① 奇数点が0個か2個のときだけ,一筆書きで図形が書ける。
② 奇数点が2個あったら,その一つから書き始めなければいけない。
③ 偶数点ばかりだったら,どこから書き始めてもよい。
ということね。
日の字形は,奇数点が2個だから,奇数点を出発点にすれば書けるわけね。目の字形は,奇数点が4個あるから書けないのだ。」
「それじゃ,あのケーニヒスベルクの橋の奇数点を数えてみよう。えーと,3本の線が出ているところが4ヵ所だから,奇数点が4個もあるじゃないか。これじゃあ,いくら考えても一筆書きができないはずだね。」
秀夫君は,なぞがとけたのでとてもうれしそうにいいました。
「オイラーさんも同じ説明をしたのかしら?」
と恵美子さんがいうと,工作君がすぐこたえました。
「きっとそうだよ,ぼくたちも数学者の一員だ。」(笑)
恵美子さんが感心したようにいいました。
「おもしろいわね。算数や数学の問題ってとける問題ばかりかと思ったら,できないっていうのを証明するのも算数・数学なのね。」
次の図形は一筆書きで書けるでしょうか。書けるかどうか予想をしてから,実際にためしてみましょう。
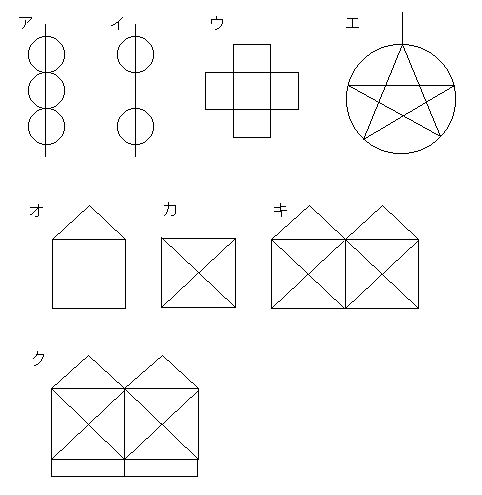
「できそうでできない」または「できなさそうでできる」というような一筆書きの問題を作って友だちとときあいっこしてみましょう。