9.関数電卓(三角関数)の活用(1/4)
ここでは傾いた穴位置、又は接点・交点等の計算に便利な三角関数の説明したいと思います。
※電卓の基本的な練習は関数電卓で三角関数を練習する。
1 通常の電卓で計算できるもの
1.1 図面例
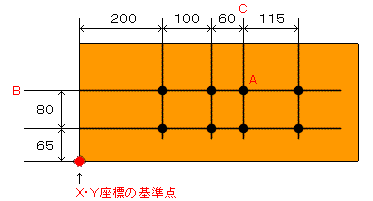 |
1.2 各基準点からの座標出しの計算例
1)穴AのC位置=200+100+60=360(X方向)
穴AのB位置=65+80=145(Y方向)
※これは単純に足し算でいいですね。
2.通常の電卓では計算出来ないもの
2.1 図面例
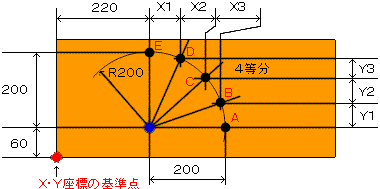 |
2.2 計算出来ない穴
穴AとEは単純に計算できますが、B・C・Dが足算だけでは出来そうもありません。
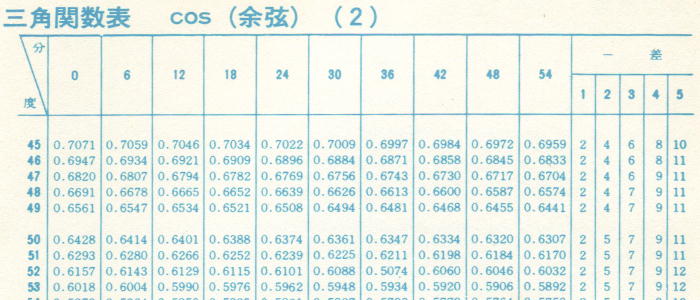
※下表のような三角関数表 というものを使えば出来ますが、最近は殆ど見かけないと思います。この場合、ルートとかラジアン、または本題の三角関数を使用します。
 |
2.3 実際の計算
それでは上記2の2.1にあるX1~3Y1~3の長さ計算して出しましょう。
※ 三角関数ってどうやって計算するの?、という方はこちらでまず勉強しまししょう。
1)見易いように直角三角形を描く
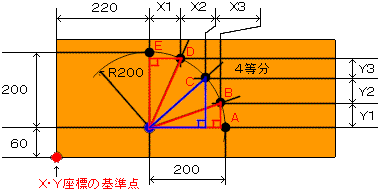 |
2)直角三角形の45度以下の所をθとして角度を入れる。
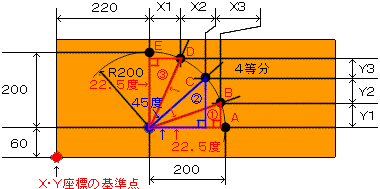 |
これを下図のように分かりやすくします。
3)直角三角形を個々に描く。
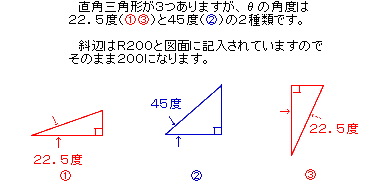 |
| 前へ | 次へ(2/4へ行く) |
トップ→MCの話→●9.関数電卓(三角関数)の活用(1/4)
© 2000 natuo