幾何公差
5.-7/7 幾何偏差の定義及び表示(JIS B 0621-1964)
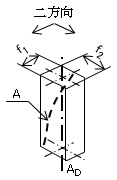
(b) データム軸直線に対する互いに直角な二方向の対称度 データム軸直線に対する互いに直角な二方向の対称度は、その二方
向にそれぞれ垂直で、データム軸直線(AD )に対して対称な幾何学的平行二平面でその軸線(A)を挟んだときの、二平面の間隔
(f1,f2 )(すなわち、二組の平行二平面で区切られる直方体の二辺の長さ)で表す(図34)。
| 図34 |
 |
(2) 中心面の対称度
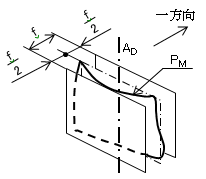
(a) データム軸直線に対する一方向の対称度 データム軸直線に対する一方向の対称度は、その方向に垂直でデータム軸直線(AD )
に対して対称な幾何学的平行二平面でその中心面(PM )を挟んだときの、二平面の間隔(f)で表す(図35)。
| 図35 |
 |
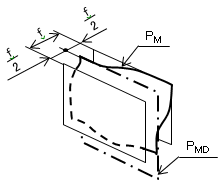
(b) データム中心平面に対する対称度 データム中心平面に対する対称度は、データム中心平面(PMD )に対して対称な幾何学的平
行二平面でその中心面(PM )を挟んだときの、二平面の間隔(f)で表す(図36)。
| 図36 |
 |
5.13 円周振れ 円周振れは、指定した方向によって、それぞれ次に示すような、対象物の表面上の各位置における振れのうち、その最大値で表す事を原則とし、円周振れ_mm又は円周振れ_μmと表示する。
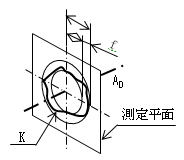
(1) 半径方向の振れ 半径方向の円周振れは、データム軸直線(AD )に垂直な一平面(測定平面)内で、データム軸直線から対象とした表面(K)までの距離の最大値と最小値との差(f)で表す(図37)。
| 図37 |
 |
(2) 軸方向の円周振れ 軸方向の円周振れは、データム軸直線(AD )から一定の距離にある円筒面(測定円筒)上で、データム軸直線に垂直な一つの幾何学的平面(PA )から対称とした表面(K)までの距離の最大値と最小値との差(f)で表す(図38)。
| 図38 |
 |
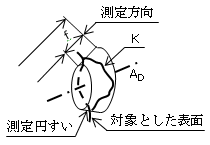
(3) 斜め法線方向の円周振れ 斜め法線方向の円周振れは、対称とした表面に対する法線がデータム軸直線に対してある角度をもつ場合、その法線を母線とし、データム軸直線(AD )を軸とする一つの円すい面(測定円すい)上の頂点から対象とした表面(K)までが距離の最大値と最小値との差(f)で表す(図39)。
| 図39 |
 |
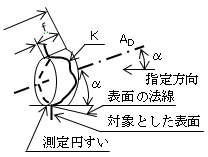
(4) 斜め指定方向の円周振れ 斜め指定方向の円周振れは、指定した方向が対象とした表面の法線方向にかかわりなく一定で、かつ、データム軸直線(AD )に対してある角度(α)をもつ場合、その方向を与える直線を母線とし、データム軸直線を軸とする一つの円すい面(測定円すい)上で、頂点から対象とした表面(K)までの距離の最大値と最小値の差(f)で表す(図40)。
| 図40 |
 |
5.14 全振れ 全揺れは、指定した方向によって、それぞれ(1)又は(2)に示すように表し、全揺れ_mm又は全揺れ_μmと表示する。
(1) 半径方向の全振れ 半径方向の全振れは、データム軸直線に垂直な方向で、データム軸直線から対象とした表面までの距離の最大値と最小値との差で表す。
(2)軸方向の全振れ 軸方向の全振れは、データム軸直線に平行な方向で、データム軸直線に垂直な一つの幾何学的平面から対象とした表面までの距離の最大値と最小値との差で表す。
| 前へ | 次へ |
トップ→幾何公差→●5.-7/7 幾何偏差の定義及び表示
© 2000 natuo