幾何公差
5.-2/7 幾何偏差の定義及び表示(JIS B 0621-1964)
4.8 直角度 直角度とは、データム直線又はデータム平面に対して直角な幾何学的直線又は幾何学的平面からの直角であるべき直線形体又は平面形体の狂いの大きさをいう。
4.9 傾斜度 傾斜度とは、データム直線又はデータム平面に対して理論的に正確な角度をもつ幾何学的直線又は幾何学的平面からの理論的に正確な角度をもつべき直線形体または平面形体の狂いの大きさをいう。
4.10 位置度 位置度とは、データム又は他の形体に関連して定められた理論的に正確な位置からの点、直線形体又は平面形体の狂いの大きさをいう。
4.11 同軸度 同軸度とは、データム軸直線と同一直線上にあるべき軸線のデータム軸直線からの狂いの大きさをいう。
備考 平面図形の場合には、データム円の中心に対する他の円形形体の中心の位置の狂いの大きさを同心度という。
4.12 対称度 対称度とは、データム軸直線又はデータム中心平面に関して互い対称であるべき形体の対称位置からの狂いの大き
さをいう。
4.13 円周振れ 円周振れとは、データム軸直線を軸とする回転面をもつべき対象物又ははデータム軸直線に対して垂直な円形平面であるべき対象物をデータム軸直線の周りに回転したとき、その表面が指定した位置又は任意の位置で指定した方向(3)に変位する大きさをいう。
注(3) 指定した方向とは、データム軸直線と交わりデータム軸直線に対して垂直な方向(半径方向)、データム軸直線に平行な方向(軸方向)又はデータム軸直線と交わりデータム軸直線に対して斜め方向(斜め法線方向及び斜め指定方向)をいう。
4.14 全振れ 全振れとは、データム軸直線を軸とする円筒面をもつべき対象物又はデータム軸直線に対して垂直な円形平面であるべき対象物をデータム軸直線の周りに回転したとき、その表面が指定した方向(4)に変位する大きさをいう。
注(4) 指定した方向とは、データム軸直線軸と交わりデータム軸直線に対して垂直な方向(半径方向)又はデータム軸直線に平行な方向(軸方向)をいう。
5.表示
5.1 真直度 真直度は、直線形体が占める領域の大きさによって、次に示すように表し、真直度 _mm又は真直度_μmと表示する。
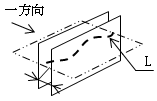
(1) 一方向の真直度 一方向の真直度は、その方向に垂直な幾何学的に正しい二平面(以下、幾何学的二平面という。)でその直線形体(L)を挟んだとき、平行二平面の間隔が最小になる場合の二平面の間隔(f)で表す(図1)。
| 図1 |
 |
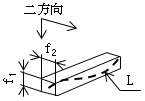
(2) 互いに直角な二方向の真直度 互いに直角な二方向{例えば5.1(1)の備考の水平方向及び鉛直方向}の真直度は、その二方向にそれぞれ垂直な二組の幾何学的平行二平面でその直線形体(L)を挟んだとき、二組の平行二平面の各々の間隔が最小となる場合の、二平面の間隔(f1、f2 )(すなわち、二組の平行二平面で区切られる直方体の二辺の長さ)で表す(図2)。
| 図2 |
 |
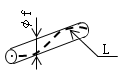
(3) 方向を定めない場合の真直度 方向を定めない場合(例えば、円筒の軸線など)の真直度は、その直線形体(L)をすべて含む幾何学的円筒のうち、最も径の小さい円筒の直径(f)で表す(図3)。
| 図3 |
 |
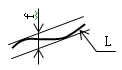
(4) 表面の要素としての直線形体の真直度 表面の要素としての直線形体(回転面の母線や、平面形体の表面に垂直な平面による断面輪郭線など)の真直度は、幾何学的に正しい平行な二直線(以下、幾何学的平行二直線という。)で、その直線形体(L)を挟んだとき、平行二直線の間隔が最小になる場合の、二直線(f)で表す(図4)。
| 図4 |
 |
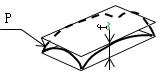
5.2 平面度 平面度は、平面形体(P)を幾何学的平行二平面で挟んだとき、平行二平面の間隔が最小となる場合の、二平面の間隔(f)で表し(図5)、平面度_mm又は平面度_μmと表示する。
| 図5 |
 |
| 前へ | 次へ |
トップ→幾何公差→●5.-2/7 幾何偏差の定義及び表示
© 2000 natuo