幾何公差
4.-2/3 普通幾何公差
b.直角度
直角を形成する二辺のうち長い方の辺をデータムとする。二つの辺が等しい呼び長さの場合には、いずれの辺をデータムとしてよい。
直角度の普通公差(単位mm)
|
公差等級 |
短 い 方 の 辺 の 呼 び 長 さ の 区 分 |
|||
|
100以下 |
100を超え |
300を超え |
1000を超え |
|
|
300以下 |
1000以下 |
3000以下 |
||
|
直 角 度 公 差 |
||||
|
H |
0.2 |
0.3 |
0.4 |
0.5 |
|
K |
0.4 |
0.6 |
0.8 |
1 |
|
L |
0.6 |
1 |
1.5 |
2 |
c.対称度
二つの形体のうち長い方をデータムとする。これらの形体が等しい呼び長さの場合には、いずれの形体をデータムとしてもよい。
対称度の普通公差は、次の場合に適用する(下図参照)。
・少なくても二つの形体の一つが中心平面をもつとき。
・二つの形体の軸線が互いに直角であるとき。
附属書B5(参考)
対称度の普通公差の例
データム:長い方の形体(L2)
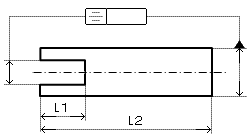 |
データム:長い方の形体(L1)
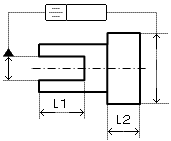 |
データム:長い方の形体(L2)
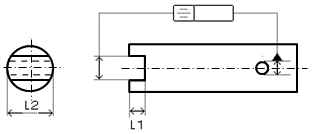 |
データム:長い方の形体(L1)
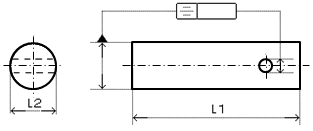 |
対称度の普通公差(単位mm)
|
公差等級 |
呼 び 長 さ の 区 分 |
|||
|
100以下 |
100を超え |
300を超え |
1000を超え |
|
|
300以下 |
1000以下 |
3000以下 |
||
|
対 称 度 公 差 |
||||
|
H |
0.5 |
|||
|
K |
0.6 |
0.8 |
1 |
|
|
L |
0.6 |
1 |
1.5 |
2 |
d.同軸度
同軸度の普通公差は規定しない。
ただし、同軸度は、半径方向の円周振れが同軸度と真円度とからなるので、極端は場合には、下表の「円周振れの普通公差」の円周振れ公差の値と同じ大きさでよい。
円周振れの普通公差(参考)
|
公差等級 |
円周振れ公差 |
|
H |
0.1 |
|
K |
0.2 |
|
L |
0.5 |
e.円周振れ
円周振れの普通公差に対しては、図面上ひ支持面が指定されている場合には、その面をデータムとする。
支持面が指定されていない場合には、半径方向の円周振れに対して、二つの形体のうち長い方をデータムとする。
二つの形体の呼び長さが等しい場合には、いずれの形体をデータムとしてよい。
円周振れの普通公差(単位mm)
|
公差等級 |
円周振れ公差 |
|
H |
0.1 |
|
K |
0.2 |
|
L |
0.5 |
| 前へ | 次へ |
トップ→幾何公差→●4.-2/3 普通幾何公差
© 2000 natuo