幾何公差
3.16 最小実体公差方式(まるL)
最小実体公差方式(LMR)は、対象とする形体がその最小実体状態(LMC)から離れるときに、指示した幾何公差を増加させることができる。つまり、体積が最小の状態から、増える方向になると、俗に言われるボーナス公差が付加され加算されるというものです。
最小実体公差方式(LMR)は、穴等の周囲の厚さや、リブのボス等一定以上の厚みを確保するときに有効です。
1.用語解説
1.1 最小実体状態(LMC)
形体のどこにおいても、その形体の実体が最小となるような許容限界寸法、例えば、最大の穴径、最小の軸径をもつ形体の
状態
1.2 最小実体寸法(LMS)
形体の最小実体状態を決める寸法
2. 最小実体状態(LMC)とは。
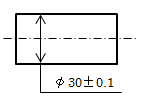
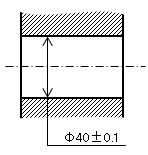
軸は許容される最小寸法で、穴は許容される最大寸法で最小実体状態になります。
|
|
軸 |
穴 |
|
図例 |
 |
 |
|
最小実体状態(LMC) |
φ29.9 |
φ40.1 |
|
最大実体状態(MMC) |
φ30.1 |
φ39.9 |
※1. 最小実体公差方式と最大実体公差方式の実体状態は、体積の最小、最大が真逆になりますからご注意下さい。
2. MMRもLMRも実体状態が基準になり、公差が緩和されます。
3. 例
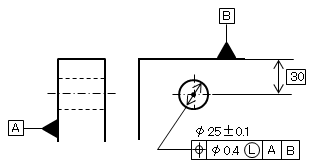
3.1 最小肉厚を位置度で示してある場合(端面と穴)
a) 図面例
公差域にまるLを適用すると、位置度φ0.4 は、穴25は最小実体状態のφ25.1にのみ適用され、穴の大きさが小さくなれ
ばその分だけ公差が緩和される。
 |
b) 必要とする最小肉厚の計算(下図参照)。
30-(25.1+0.4) / 2=17.25
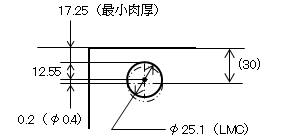 |
※ 穴がφ24.9(MMC)の場合、25.1-24.9で0.2小さくなるので、位置度はφ0.4にφ0.2加算されφ0.6になる。
c) 公差線図
|
穴径(φ) |
位置度(φ) |
|
24.9 (MMC) |
0.6 |
|
24.95 |
0.55 |
|
25.0 |
0.5 |
|
25.05 |
0.45 |
|
25.1 (LMC) |
0.4 |
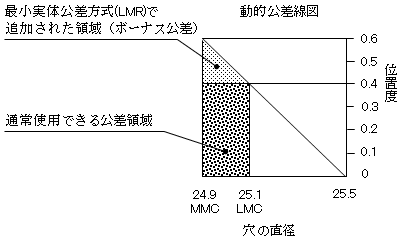 |
※穴径φ24.9では、部品の体積が最大となり、最小肉厚17.25も確保されます。
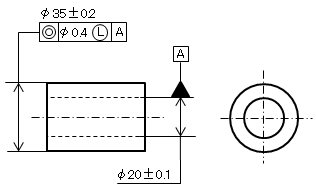
3.2 段のある軸の同軸度
公差域にまるLを適用すると、同軸度φ0.4は最小実体状態のφ34.8にのみ適用され、円筒の直径が大きくなるにつれ、公差値が緩和できます。
a)図面例
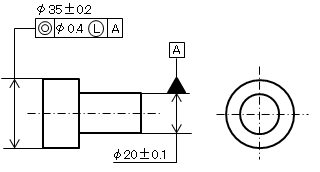 |
※ 最小幅(厚さ)確保に使えるます。
b) 必要とする最小厚さの計算(下図参照)
((34.8-0.4)-20.1) /2=7.15
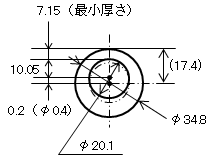 |
c) 公差線図
|
円柱の直径(φ) |
公差域(φ) |
|
35.2 (MMC) |
0.8 |
|
35.1 |
0.7 |
|
35.0 |
0.6 |
|
34.9 |
0.5 |
|
34.8 (LMC) |
0.4 |
※穴が35.2(MMC)の場合、35.2-34.8でφ0.4大きいので、同軸度はφ0.4に0.4加算されφ0.8 になります。
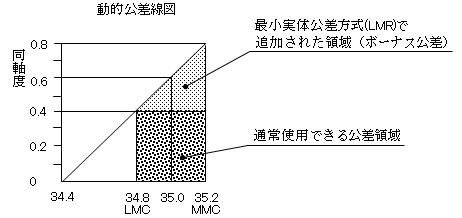 |
※軸径35.2は体積が最大になるので最大実体状態(MMC)になります。
4. パイプの肉厚確保の場合例
この場合も上記3.2の段のある軸の同軸度と同じ理屈、同じ結果になります。
 |
| 前へ | 次へ |
トップ→幾何公差→●3.16 最小実体公差方式(まるL)
© 2000 natuo