幾何公差
3.15-2/2 最大実体公差方式(まるM)
2)解釈
a)公差値と公差値横のまるM
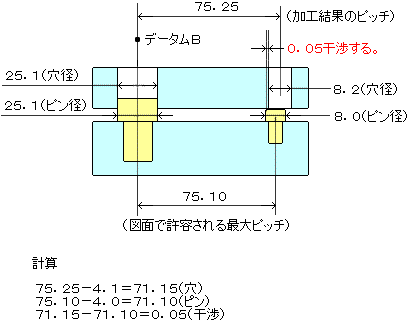
下図完成品は、わく75が75.25なので、公差値φ0.2から外れ、さらに公差値横の
まるMを使っても救済出来ない状況での説明になります。
 |
NG(下図参照)になります。
 |
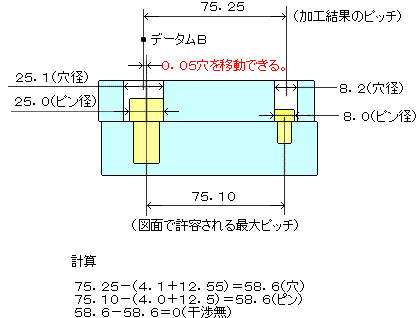
b)上記の救済にデータムBのまるMを使います。
データムBをピンと穴径の差0.1の半分0.05を左にずらします(下図参照)。
 |
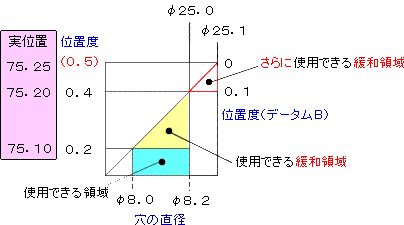
c)動的公差線図
上記の説明は、下記のような理屈になります。
注、赤枠内がさらに使用できる緩和領域になります。
 |
尚データム横のまるМを動的公差線図で説明しているのは、私独自の表現になります。
d)備考
ここでは単純に加工穴一個を一方向で説明しましたが、複数ある場合は相応な手間がかかると思います。
また加工穴が沢山ある場合で、データムのまるMを使う場合は加工穴の公差値プラス横のまるMの実効状態の境界を守らなければいけませんので注意して下さい。
※最後の手段でデータムBをずらすと言うことですので、可能ならどちらのまるMも使わなくてもいいような作業を推奨します。
3.公差値が0(ゼロ幾何公差方式)の場合
1)下図のように、公差値に許容値が無い場合の解釈
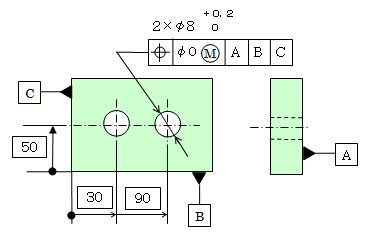 |
穴の位置度の許容差はありませんが、まるMの最大実体公差が適用されます。 |
2)穴径と位置度の関係
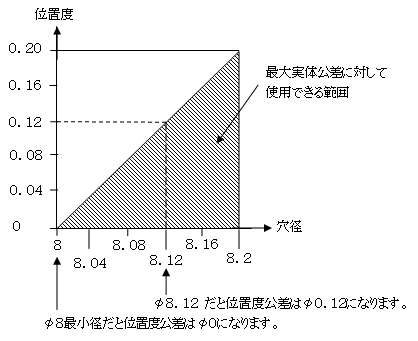 |
公差値に公差が記入されていれば余裕があるのですが、公差値φ0の場合は左図のように最小径では余裕がありません。 |
※この場合、加工された穴径が位置度を左右しますので、加工側の注意が必要になります。
4.備考
最大実体公差は、真直度・平行度・直角度・傾斜度・位置度・同軸度・対称度の7種類に適用できますが、寸法公差の付いた形体の軸線又は中心面に限ります(平面や表面上の線には適用できません)。
※平面度・真円度・円筒度・輪郭度(線、面)・振れ(円周、全)には使用出来ません。
5.用語解説(JISB0023から抜粋)
今回殆ど使っていませんが・・・・。
実効寸法(VS)
形体の実効状態を決める寸法
最大実体寸法(MMS)
形体の最大実体状態を決める寸法
動的公差線図
公差域の変化を現した表
最大実体状態(MMC)
形体のどこにおいても、その形体の実体が最大となるような許容限界寸法、たとえば、最小の穴径、最大の軸径を持つ形態
最小実体状態(LMC)
形体のどこにおいても、その形体の実体が最小となるような許容限界寸法、例えば、最大の穴径、最小の軸径をもつ形体の状態
局部実寸法
形体の任意の断面における個々の距離、すなわち、任意の相対する2点間で測定した寸法。
実効状態(VC)
図面指示によってその形体に許容される完全形状の限界であり、この状態は、最大実体寸法と幾何公差との総合効果によて生じ
る。
最小実体寸法(LMS)
形体の最小実体状態を決める寸法。
| 前へ | 次へ |
トップ→幾何公差→●3.15-2/2 最大実体公差方式(まるM)
© 2000 natuo