幾何公差　メイン　３．１２対称度

直下の“検索イン時クリック”をクリックして頂くとページ全体が表示されます。

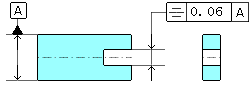
幾何公差
３．１２対称度（右側定義と解釈参照）
１）図示例と理屈
ア、溝位置の図示例

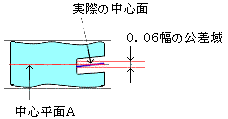
データム中心平面Aに対し、対称に置かれた幅0.06の平行2平面に溝の中心平面があればよい

実際の理屈は下図のようになります。

振り分けで幅0.06の2平面内に入っていればOK

※参照する面にうねりがある場合、最大隙間が最小になるようにし、その中心をデータムＡにします。

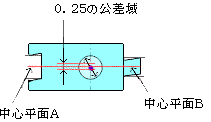
イ、溝とボスがデータム時の穴位置図示例

共通データム中心平面A-Bに対し、対称に置かれた幅0.25の平行2平面に穴の中心があればよい。

実際の理屈は下図のようになります。

振り分けで幅0.25の2平面内に入っていればOKです。

※データムＡ及びＢの形状が変形としていれば、その接触面を最大幅とし、その中心平面を共通データムとします。
　
２）検証方法
定盤でもそのまま出来ますが、機能ゲージが必要になる場合があります。三次元測定器で検証可能ならその方が宜しいかと思います。

３）備考
データムは１つしか設定出来ませんので、２つ必要な場合は共通データムとして下さい。

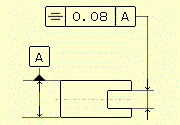
公差域の定義
　公差域は、t だけ離れ、データムに関して中心平面に対称な平行二平面によって規制される。

図示例と解釈
　実際の（再現した）中心平面は、データム中心平面Aに対称な0.08㎜だけ離れた平行二平面の間になければならない。