幾何公差　メイン　３．１０

直下の“検索イン時クリック”をクリックして頂くとページ全体が表示されます。

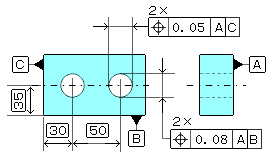
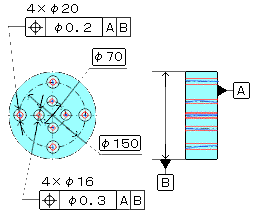
幾何公差
３．１０－２/２位置度（右側定義と解釈参照）
２）中心線の規制で公差値にφ無い場合
ａ、図面例

指示線の方向に公差値だけ離れた２平面間が公差域になる。

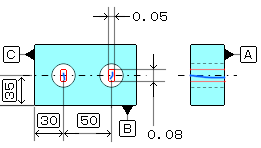
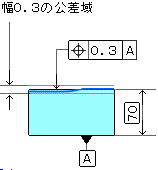
ｂ、公差域例

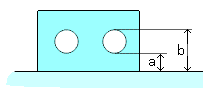
各穴はデータムA面に直角で、データムBから正確に35ミリ離れた面に対称に置かれた幅0.08の2平面とデータムCから30ミリ及びその穴から50ミリ離れた面に対称に置かれた幅0.05の2平面内の公差域に入っていなければいけない。

　　　　　　　　
ｃ、測定例

aとbを測定し、穴径を半分にして、
aにプラス、又はbから引き、理論値に対して差異を出し2倍にする。

ｄ、測定結果例　　

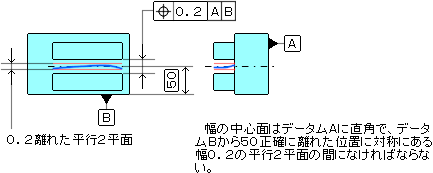
　　　※穴位置が公差内で倒れている場合もありますが、通常入り口又は中央等任意の
　　　　位置で測定し評価すればいいと思います。

３）中心面の位置度

４）同軸に配置された形体の場合

位置度公差付き形体が円周上に配列されている場合には、特別な指定がない限り、等分に配置されていて正確な位置にあると解釈する。

φ20とφ16各4箇所の軸線はデータムAに直角で、データム軸直線Bから理論的に正確な位置にある、φ16はφ0.3、φ20はφ0.2の円筒公差域内に入っていなければならない。

　　　　　
５）平たん面の位置度

データム平面Aに平行で、Aから70ミリ離れた理論的に正確な位置に対称に置かれた幅0.3の平行2平面に入っていなければならない。

傾いた、あるいは直角な面にも使えます。

　　　　　　　　
６）以外の位置度
　けがき線・球などもに適用することができます。

７）備考
　幾何公差でも一番使われると思われる位置度ですね。
データムは必要に応じて指定した方が、製図側また加工および評価する側ともわかりやすいでしょう。

実際の検査は、定盤上でハイトゲージとハイトマスターでも可能ですが、最近流行の三次元測定器でしょうか。　