幾何公差　メイン　３．１０

直下の“検索イン時クリック”をクリックして頂くとページ全体が表示されます。

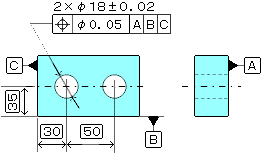
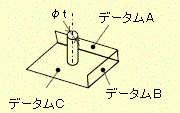
幾何公差
３．１０－１/２位置度（右側定義と解釈参照）　
※JIS B 0025（規格名称製図―幾何公差表示方式―位置度公差方式）も参照の事。
１）、中心線の規制で公差値にφがある場合
ａ、データムが３つある場合の図面例と公差域例

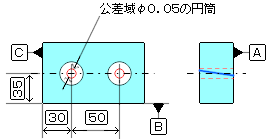
　　　公差域例
　　　※赤が公差域で青が実際の位置（以下同じ）

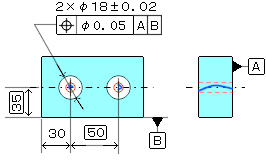
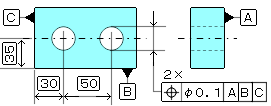
各穴の中心軸線は、データムAに対して直角で、データムBから35ミリ及びデータムCから30mmとその右横の50ミリ離れた位置にあるφ0.05の円筒公差域の中に入らなければいけない。

ｂ、データムが２つある場合の図面例と公差域例

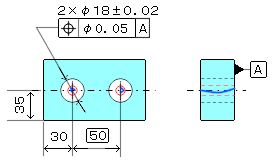
各穴の中心軸線は、データムAに対して直角で、データムBから35ミリ離れ互いに50ミリ離れた位置にあるφ0.05の円筒公差域の中に入らなければいけない。

左端面からの位置は規制されないので注意。

c、データムが１つの場合の図面例と公差域例

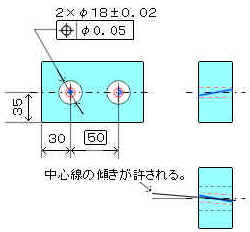
各穴の中心軸線は、データムAに対して直角で、正確に50ミリ離れたφ0.05の円筒公差域の中に入らなければいけない。

左端面と下面からの位置は規制されないので注意。

d、データムが無い場合の図面例と公差域例

各穴の中心軸線は、正確に50ミリ離れたφ0.05の円筒公差域の中に入らなければいけない。

公差領域の円筒はプレートの底面・端面・側面に対する姿勢が規制されない（底面に対して90度とは限らない）ので注意を要します。

e、一見すると２平面の公差域のようだけど公差値にφがある場合。

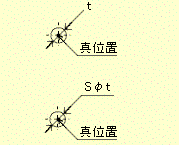
公差値にφがある場合、指示線の向きは意味がなくなり、公差域は円筒になります。

※公差域の説明は上記ａ、の公差域例と同じになりますが、円筒の大きさはφ０．１になります。

位置度公差１
公差域の定義
厚みが無い場合（２次元）
　公差域は、対象としている点の理論的に正確な位置を中心とする直径 t の円の中又は球の中の領域である。

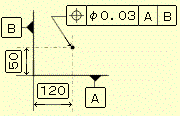
図示例と解釈
　指示線の矢で示した点は、データム直線Aから50㎜、データムBから120㎜離れた真位置を中心とする直径0.03㎜の円の中になければならない。

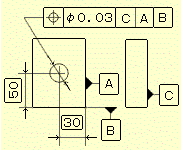
※以降は通常通り厚みがある場合を示す。

公差値にφがある場合
公差域の定義
　公差域は直径 t の円筒によって規制される。その軸線はデータムC、A及びBによって理論的な正確な寸法によって位置づけられる。

指示方法及び説明
　実際の（再現した）軸線は、その穴の軸線がデータムC、A及びBに関して、理論的に正確な位置にある直径0.03の円筒公差域の中になければならない。

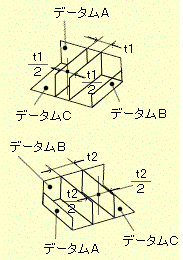
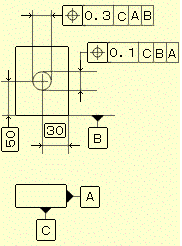
公差数値にφが無い場合は下記の「位置度公差２」で説明しています。

位置度公差２
公差値にφが無い場合
　公差域は、それぞれ距離 t1 及び t2 だけ離れ、その軸線に関して対称な2対の平行二平面によって規制される。その軸線は、それぞれデータムA、B及びCによって理論的に正確な寸法によって位置づけされる。公差は、データムに関して互いに直角な二方向で指示される。

指示方法及び説明
　実際の軸線は、上下方向に0.1(t1)、左右方向に0.3(t2)だけ離れ
、それぞれ直角な個々の2対の平行二平面の間になければならない。平行二平面の各対は、データム系に対して正しい位置に置かれる。