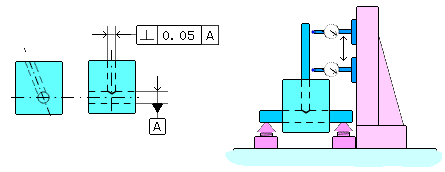
| 幾何公差 3.8 直角度(右側定義と解釈参照) 1)図示例と検証方法例 ア、角物の場合 その1
その2 円柱にダイヤルゲージを馬乗りさせ、このようにして任意の高さの面を測り、その最大差を直角度とする。
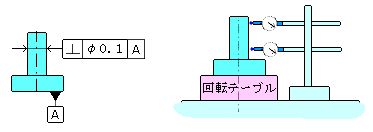
その3 数値化は難しいですが、スコヤでも出来ます。 イ、穴がデータムで傾きある穴の場合 データムAにマンドレルを挿入し、定盤と平行にすると同時に、イケールと直角になるように置く。測定すべき穴にも隙間のないマンドレルを入れ、上下を測定したときの最大差を直角度とする。
ウ、円筒の場合 回転テーブルに測定物を置き、回転テーブルと円筒部の一端の回転軸線を合わせ、所要の数の断面でテーブルを1回転回して、読みの最大差の半分を直角度とする。
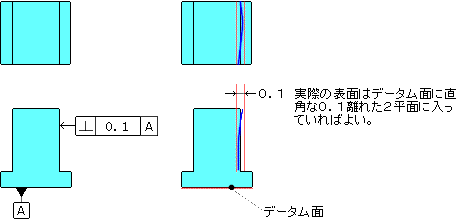
2)図示例と公差領域例 ア、角物の場合
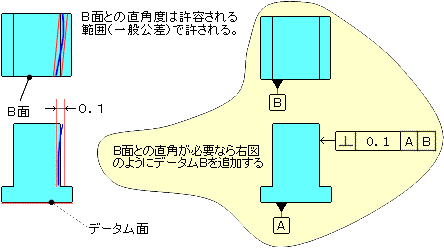
イ、円筒の場合
3)備考 ・平面に対する真直度は2直線の間でしたが、直角度は2平面の間になります。 ・測定は3次元測定機が一番簡単かと思います。 |
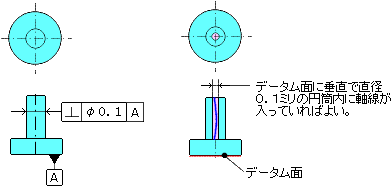
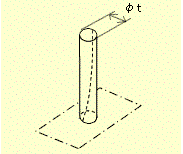
公差域の定義 公差の示す数値の前に記号φがついている場合には、この公差域は、データム平面に垂直な直径 t の円筒の中の領域である。
図示例とその解釈 指示線の矢で示す円筒の軸線は、データム平面Bに垂直な直径0.01㎜の円筒内になければならない。
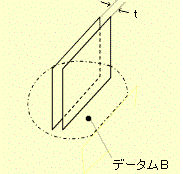
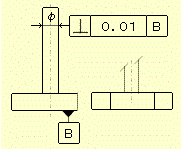
公差域の定義2 公差の示す数値の前に記号φがついていない場合
指示方法及び定義 実際の円筒の軸線は、0.01だけ離れ、データム平面Bに直角かつ 指示線の矢の方向の平行二平面の間になければならない。
|
| 前へ | 次へ |
トップ→幾何公差→●3.8 直角度
© 2000 natuo