直下の“検索イン時クリック”をクリックして頂くとページ全体が表示されます。

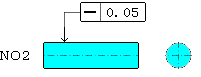
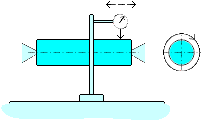
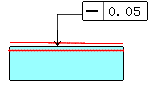
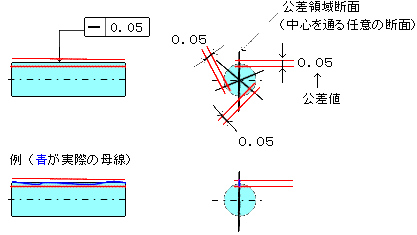
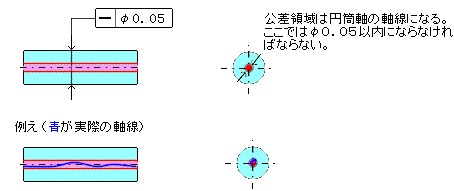
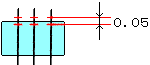
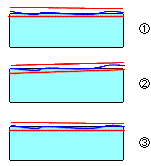
幾何公差 ３．１ 真直度（右側定義と解釈参照）　 １）図示例と検証方法例  図　示　例  検　証　方　法    直定規を最大距離が最小になるように調整し、すきまゲージなどで判定する（下図）      四角の直定規などで上記と同じ要領で判定。    定盤に両センターで支え、回転させる。完全１回転の間のダイヤルの読みの差の半分をその差の方向にとり、プロットする。必要な数の断面で同様に行う。軸の真直度は各断面中心間の最大偏差となる。   検証は、ＮＯ１・ＮＯ２とも定盤でダイヤルゲージを使った方が数値でも分かるのでお勧めです。 ２）図示例と公差領域例 公差値にφが無い場合 公差値にφがある場合 角材の場合      任意の位置で母線と直角な断面に適用されます。 　例　青が母線（実際の表面形状）      各々任意の断面の母線に適用され、以外との関連はありません。  ②は傾いていますが、JISのB 0621では、「直線形体の幾何学的に正しい直線からの狂いの大きさをいう。」と定めていますから、傾きの度合いに関係なく２直線の間に入っていればよいと解釈出来ます。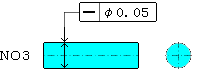 ３）備考 　４．１の１）にあるＮＯ１とＮＯ２は指示線の方向のみ規制され、ＮＯ３は公差値にφがあると同時に指示線が寸法線と一致しているので軸線の真直度を意味します。 指示線と寸法線が一致しているのか、していないかで意味も変わってきますので注意して下さい。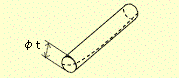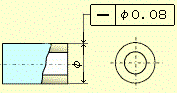  定義 　公差域が示す数値の前に、記号φがついている場合には、この公差域は直径 t の円筒の中の領域である。 図示例と解釈 　円筒の直径を示す寸法に公差記入枠が結ばれている場合には、その円筒の軸線は、直径0.08mmの円筒内になければならない。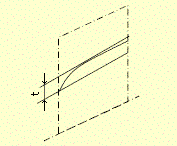 定義 　特に軸対象物の形体については、その軸線を含む平面上におけるものである。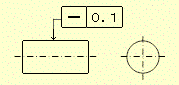 図示例と解釈１ 　指示線の矢で示す円筒上の任意の母線、その円筒の軸線を含む平面内において、0.1㎜だけ離れた二つの平行な直線の間になければいけない。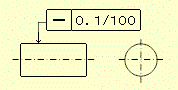 図示例と解釈２ 　指示線の矢で示す円筒面の任意の母線上で、任意に選んだ100㎜の部分は、軸線を含む平面内において、0.1㎜だけ離れた二つの平行な直線の間になければならない。 前へ  次へ トップ→幾何公差→●３．１真直度 © 2000　natuo