正三角形の三垂線の定理の性質を利用した三角グラフを使って、日常生活で出てくる
データーを分析することで、数学の有用性を感じることが、この教材のねらいである。
社会科で、例えばある県の産業の割合(第一次産業、第二次産業、第三次産業)を表すのに、
三角グラフを使う。これは、「正三角形の内部の点から3辺までの距離の和が一定である。」
という三垂線の定理を利用して表現するグラフである。
三垂線の定理については、数学Aの「3つのどの場所からも便利な場所」に詳しく解説してい
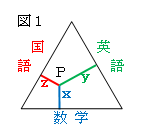
る。例えば図1のように、ある生徒の数学、国語、英語の点数の割合をグラフに表すときに、

高さを100%として、
x=(数学の点数)÷(3教科の合計点)
y=(国語の点数)÷(3教科の合計点)
z=(英語の点数)÷(3教科の合計点)
として長さをとると、点Pを打つことができる。
ある生徒の実力テストが国語が40点、数学が90点、英語が70点だとすると、
x=90÷200=0.45,y=70÷200=0.35,z=40÷200=0.2より、
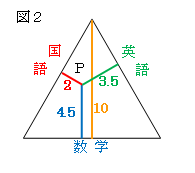
正三角形の高さを10cmとすると、x=4.5cm,y=3.5cm,z=2cm
にとり、この生徒の実力テストの結果を表した三角グラフは、
図2のようになる。
このグラフから、この生徒は数学が得意で理系向きであるなどと
分析することができる。
(点Pが三角形の上の方に分布すると数学が得意で理系向きなど)
また、割合なので、国語が20点、数学が45点、英語が35点の生徒も同じグラフになる。
つまりこのグラフは点数の割合だけを表したグラフなので、クラスで公開もしやすく、
クラスごとの分布も見ることができるのである。
4教科にしたいときは正方形、5教科にしたいときは正五角形と拡張することができる。