数学史の話を交えながら、分数で問題解決をすることで、数や計算に興味をもち、
分数の計算力を培うことが、この教材のねらいである。
文書として残っている最古の数学書は、紀元前17世紀くらいにエジプトで書かれた
「リンドパピルス」といわれている。リンドパピルスには全部で87の問題が出て
いるが、その中で「分数をわざわざ異なる分母を使った単位分数の和で表す」
というものがおもしろいので、ここで紹介する。
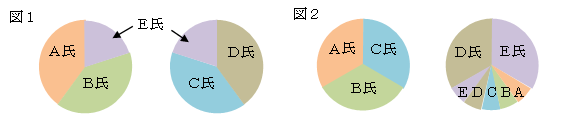
2個の円形のホットケーキを5人で分けるとき、図1のように(2/5)の形で分けると、
E氏だけ形が違ってしまうので、図2のように、とりあえず(1/3)ずつの塊で分け、
残りの(1/3)を5等分して全体の(1/15)ずつ分けると、全員同じ形になって平等である。
これを式で表すと、(2/5)=(1/3)+(1/15) ということになる。
当時は分子という考えがないらしく、リンドパピルスではすべての分数を単位分数で表して
いる。

以下のように、いろいろな分数を単位分数に分けてみるとよい。
(2/5)=(1/3)+(1/3)÷5=(1/3)+(1/15) を参考にして考えると求めやすい。
(2/3)=(1/2)+(1/2)÷3=(1/2)+(1/6)
(2/7)=(1/4)+(1/4)÷7=(1/4)+(1/28)
(3/5)=(1/2)+(1/2)÷5=(1/2)+(1/10)
また、(4/5)=(1/2)+(1/4)+(1/20) のように3つ以上の単位分数に分けることもある。