四角形の最短シュタイナー問題を使い、操作的な活動を通して身近にある課題を解決する
ことで、数学の有用性を感じることが、この教材のねらいである。
数学Aの「3つのどの場所からも便利な場所」に載せてある三角形の最短シュタイナー問題を
発展させて、四角形の最短シュタイナー問題を利用して、問題を解決する。
1辺が100mの正方形の4つの頂点に家がある。この4軒をネットワーク配線でつなぐとき、
配線の合計を一番短くするためにはどのように配線すればよいだろうか。

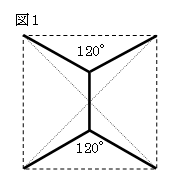
三角形の最短シュタイナー問題で考えると、
対角線でつなぐのではなく、図1のように、
対角線を引いてできた2つの三角形それぞれで
120°となる点をとって結んだものが答えである。
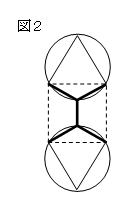
作図は、正三角形の外接円を使って、
図2のようにすると描ける。実際に考察させる
と、図3のようないろいろな案がでてくると考えられるので、
長さを計算したりはかったりして、最短なものを見つけさせるとよい。
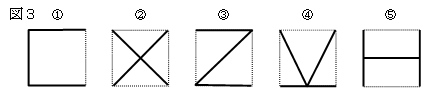
図1の最短なものは{(100√3)/3}×4+(100-{(100√3)/3}=100(1+√3)≒273m。
図3の①と⑤は300m,②は200√2≒282m,③は200+100√2≒314m, ④は100(1+√5)≒323m。