関数を用いて過去のCDの売り上げデータから傾向を分析し、今後のCDの売り上げを予測
する活動から、数学と日常生活との関連性と数学の有用性を感じることが、この教材
のねらいである。
次の表は2003年4月以降の森山直太朗の「さくら(独唱)」という曲のCDの売り上げ枚数の推移
を表したものである。
| 週数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 売上(万枚) | 2.4 | 5.1 | 7.5 | 9.4 | 10.8 | 9.9 | 7.8 |

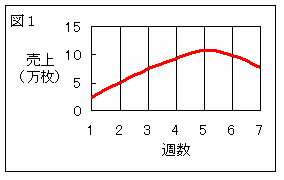
これをグラフにかくと図1のようになる。このグラフ
はどんな関数に近似するかを求める。
売り上げ枚数の差を計算してみると、
5.1-2.4=2.7 ⇒ 7.5-5.1=2.4
⇒ 9.4-7.5=1.9 ⇒ 10.8-9.4=1.4
となり、傾きがだんだん緩やかになっていて、頂点があることから、2次関数に近似できると予測できる。
そこで図1のグラフを、2次関数に近似して、最小2乗法で回帰曲線を求めてみると、
y=-(1/2)x2+5x-(5/2)のグラフに近似できる。これを平方完成すると、
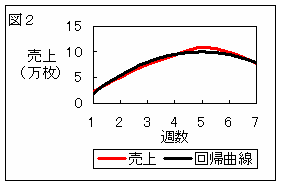
y=-(1/2)(x-5)2+10となり、図2のようになる。
この式を利用して、この曲の8週目の売り上げを
予測する。計算によると、
y=-(1/2)(8-5)2+10=5.5となり、
実際の売り上げは、5.4万枚だったため、
かなり近い予測ができたといえる。
ただし、この2次関数はx=10のときにyの値が負に
なるため、局所的な近似になる。
CDの売り上げが分析できると、来週の売上げの予測や、次に同じような曲を出すときの
売り上げの推移が予測でき、CDを何枚作って何枚出荷すればよいかなどの目安になる
と考えられる。
次の表は、2003年3月以降のSMAPの「世界で一つだけの花」という曲のCDの売り上げ枚数
の推移を表したものである。
| 週数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 売上(万枚) | 63.0 | 38.0 | 30.0 | 14.0 | 10.0 | 8.0 | 6.1 | 5.5 |
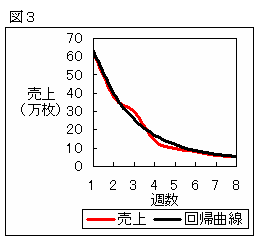
これをグラフにかくと図3のようになる。このグラフを
指数関数に近似して、最小2乗法で回帰曲線を求めて
みると、y=59.4×(0.61)x+3.6のグラフに近似できる。
図1の曲のように、徐々に売り上げを伸ばすCDは
2次関数に近似できると分析できるが、
図2の曲のように、発売1週目から売れるCDは
指数関数に近似できると分析することもできる。