球の表面積の公式の求め方

back

面積

中学校で学習した球の表面積の公式の求め方について考察することで、定積分に興味をもち、

単元の有用性を感じることが、この教材のねらいである。

①球の体積の公式の求め方

球の表面積の公式の求め方について考察する前段階として、球の体積の公式の求め方を

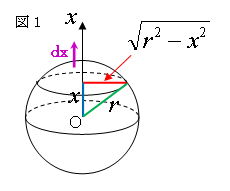
考察しておこう。下の図１において、球の中心から距離 x の点で切った断面である円の半径は

√(r²－x²) であるから、円の面積は、Ｓ(x)＝π(r²－x²) となる。

よって、球の体積Ｖは、円の面積を x 方向に積分すると、Ｖ＝２∫₀^r π(r²－x²) dx より、

Ｖ＝２π[r²x－(x³/3)]₀^r＝(4/3)πr³ を導くことができる。

②球の表面積の公式の求め方(1)

次に、球の表面積の公式の求め方について考察する。

まずは体積のときと同様にすると、図１において、

球の中心から距離 x の点で切った断面である円の

円周の長さは、Ｌ(x)＝２π√(r²－x²) となる。

よって、球の表面積Ｓは、円周を x 方向に積分すると、

Ｓ＝２∫₀^r ２π√(r²－x²) dx より、

ｘ＝rsinθ と置換すると、Ｓ＝４π∫₀^(π/2) √(r²－r²sin²θ)rcosθ dθ

　＝４πr²∫₀^(π/2) cos²θ dθ＝４πr²∫₀^(π/2)(1＋cos2θ)/2 dθ

　＝２πr²[θ＋(sin2θ/2)]₀^(π/2)＝π²r² となり、

球の表面積の公式、Ｓ＝４πr² とは違ってしまう。

これは、円周の長さを x 方向に積分するときに、ｘを微小増加させたときの表面積の変化量が

x＝0 付近と x＝r 付近で異なり、x＝r 付近の方が表面積の増加量が大きいためと考えられる。

そこで、積分方向を変えてみることにする。

③球の表面積の公式の求め方(2)

表面積の変化量が一定になるように、積分方向を

変えて、球の表面に沿って積分するように計算して

みることにする。

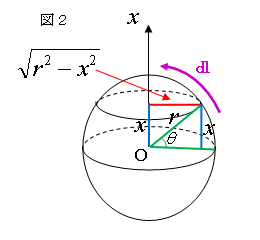
図２において円周を球の表面に沿った ｌ 方向に積分

すると、Ｓ＝２∫₀^(πr/2) ２π√(r²－x²) dｌ より、

l＝ｒθ なので、ｘ＝rsinθ と置換すると、

Ｓ＝４π∫₀^(π/2) √(r²－r²sin²θ)r dθ

　＝４πr²∫₀^(π/2) cosθ dθ＝４πr²[sinθ]₀^(π/2)＝４πr²

となり、球の表面積の公式を導くことができる。