積分を利用した重心の求め方

back

定積分と面積

いろいろな図形の重心の位置を積分を利用して求めることで、積分に興味をもち、

単元の有用性を感じることが、この教材のねらいである。

重心を求める公式がある。これは、図形の面積をSとしたとき、

重心の座標（ｘ_G，ｙ_G）は、ｘ_G＝(1/S)∫ｘds，ｙ_G＝(1/S)∫ｙdsである。

ここでdsは、それぞれの積分方向における面積の微小増加量である。

①正三角形の重心

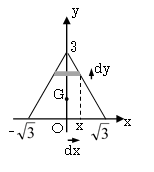
簡単な例として、この公式を使って、右図のような

一辺の長さが3の正三角形の重心を計算で求めてみよう。

面積 S＝(1/2)×2√3×3＝3√3

図の正三角形の右側の斜辺の直線の式は、y＝－(√3)x＋3、

x＝(1/√3)(3－y)より、

ｙ方向の面積の微小増加量 ds＝2xdy＝(2/√3)(3－y)dy

よって公式より、y_G＝(1/S)∫₀³yds＝(1/3√3)∫₀³y(2/√3)(3－y)dy

　＝(2/9)∫₀³(3y－y²)dy＝(2/9)[(3/2)y²－y³/3]₀³

　＝(2/9)((27/2)－9)＝(2/9)×(9/2)＝1

図形がｙ軸に対して左右対称なので、x_G＝0となり、

図のような正三角形の重心が(0,1)であることを計算で求めることができる。

②直角三角形の重心

x軸，ｙ軸，直線ｙ＝－2x＋6 で囲まれる直角三角形の重心を計算で求めてみよう。

面積 S＝(1/2)×3×6＝9

x方向の面積の微小増加量 ds＝ydx＝(－2x＋6)dx

x_G＝(1/S)∫₀³xds＝(1/9)∫₀³x(－2x＋6)dx

　＝(1/9)[－(2/3)x³＋3x²]₀³

　＝(1/9)(－18＋27)＝1

斜辺は、x＝(1/2)(6－y)より、

ｙ方向の面積の微小増加量 ds＝xdy＝(1/2)(6－y)dy

y_G＝(1/S)∫₀⁶yds＝(1/9)∫₀⁶y(1/2)(6－y)dy

　＝(1/18)[3y²－y³/3]₀⁶

　＝(1/18)(108－72)＝2

ゆえに、重心が(1,2)であることを計算で求めることができる。

③放物線で囲まれた面の重心(1)

放物線ｙ＝x²と直線ｙ＝4 で囲まれる図形の重心を計算で求めてみよう。

放物線はx＝√y より、面積 S＝2∫₀⁴(√y)dy＝2[(2/3)y^(3/2)]₀⁴＝32/3

ｙ方向の面積の微小増加量 ds＝2xdy＝(2√y)dy

y_G＝(1/S)∫₀⁴yds＝(3/32)∫₀⁴y(2√y)dy

　＝(3/16)∫₀⁴y^(3/2)dy＝(3/16)[(2/5)y^(5/2)]₀⁴

　＝(3/40)×32＝12/5

図形がｙ軸に対して左右対称なので、x_G＝0となり、

ゆえに、重心が(0,12/5)であることを計算で求めることができる。

④放物線で囲まれた面の重心(2)

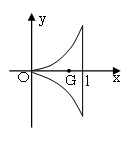
最後に右図のように、放物線ｙ＝x²と放物線ｙ＝－x²、直線x＝1

で囲まれる図形の重心を計算で求めてみよう。

面積 S＝2∫₀¹2x²dx＝[(2/3)x³]₀¹＝2/3

x方向の面積の微小増加量 ds＝ydx＝2x²dx

x_G＝(1/S)∫₀¹xds＝(3/2)∫₀¹x×2x²dx

　＝3[(3/4)x⁴]₀¹＝3/4

図形がｙ軸に対して左右対称なので、y_G＝0となり、

ゆえに、重心が(3/4,0)であることを計算で求めることができる。

①～④の図形を実際に厚紙で作り、計算で求めた点に穴をあけ、ひもを通してぶら下げて

バランスがとれるかを確かめてみるとおもしろい。