円に内接するn角形と円に外接するn角形の面積から、円の面積を考察することで、
単元のおもしろさや有用性を感じることが、この教材のねらいである。
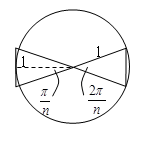
半径1の円の面積を、その円に内接するn角形と外接するn角形の面積から求める。

内接するn角形の面積は、
S=(1/2)×1×1×sin(2π/n)×n=(n/2)sin(2π/n)より、
lim(n→∞)S=lim(n→∞)[(1/2)×2π×{sin(2π/n)/(2π/n)}]= π
外接するn角形の面積は、
S=(1/2)×2tan(π/n)×1×n=n×tan(π/n)より、
lim(n→∞)S=lim(n→∞)[n×{sin(π/n)/cos(π/n)}]
=lim(n→∞)[{π/cos(π/n)}×{sin(π/n)/(π/n)}]= π
より、はさみうちの原理より、円の面積は π であることが求まる。