PSpice（評価版）でStep位相補正をＳｔｕｄｙする
     

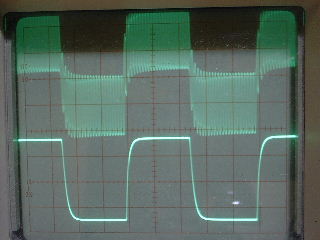
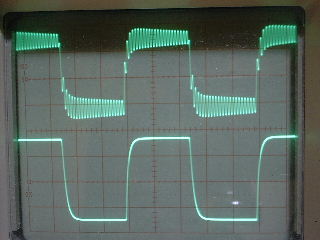
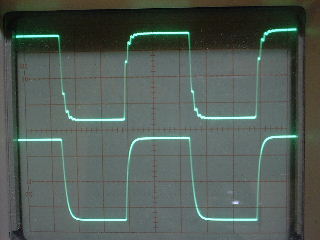
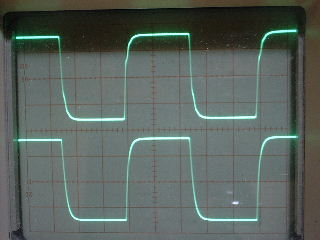
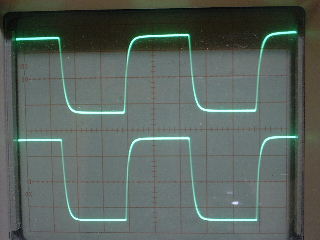
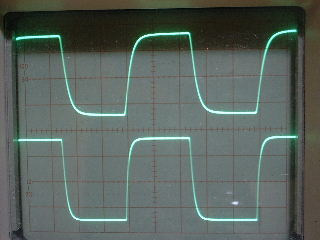
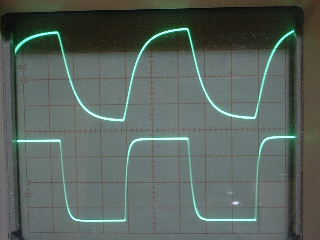
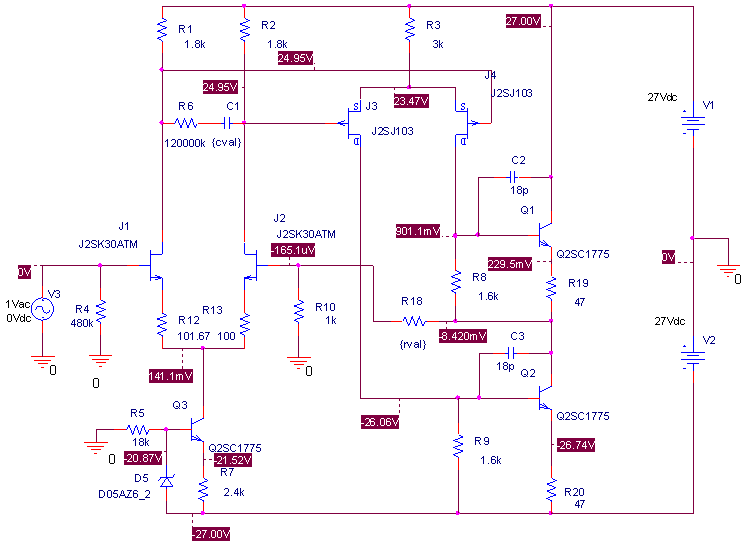
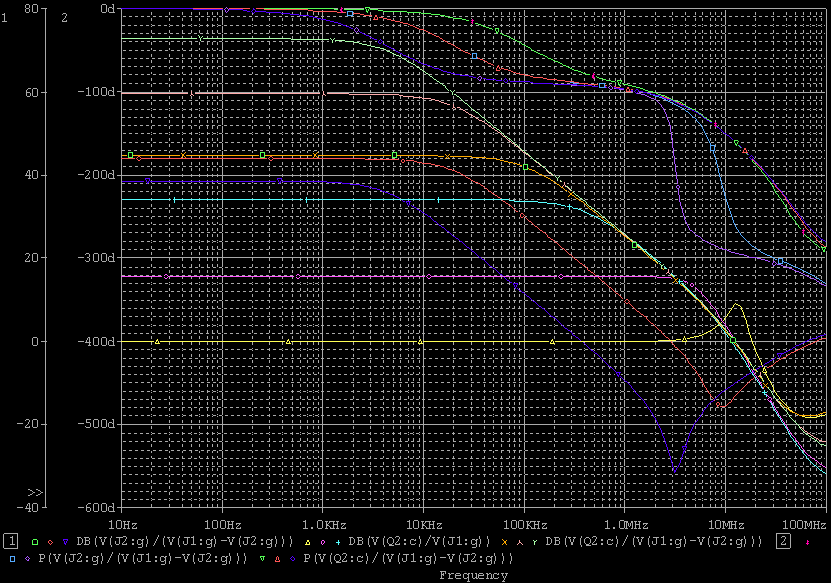
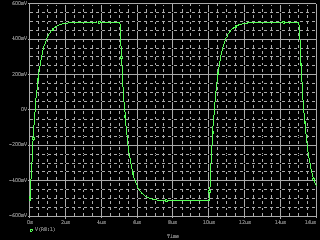
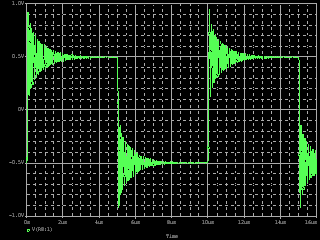
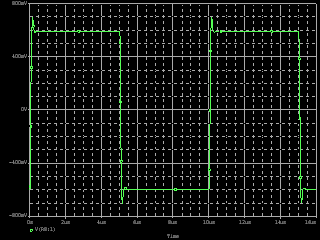
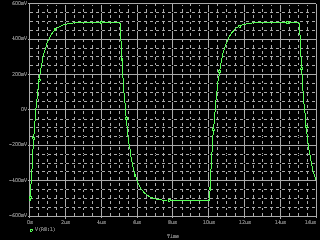
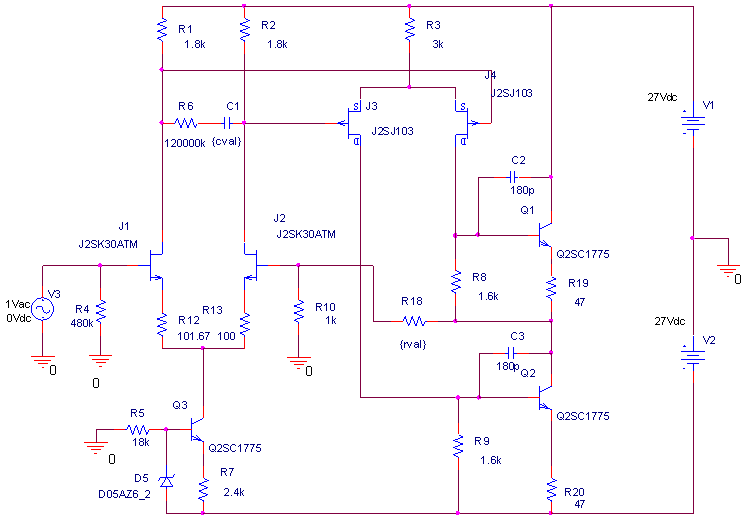
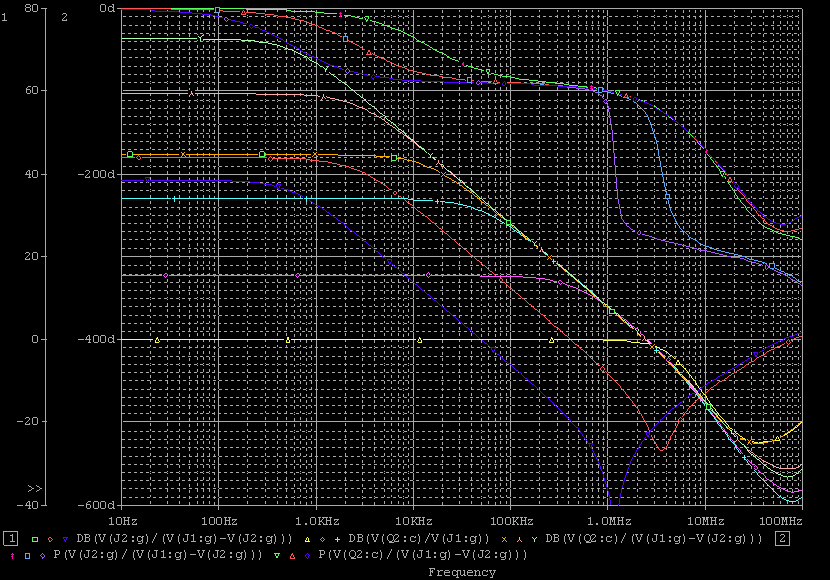
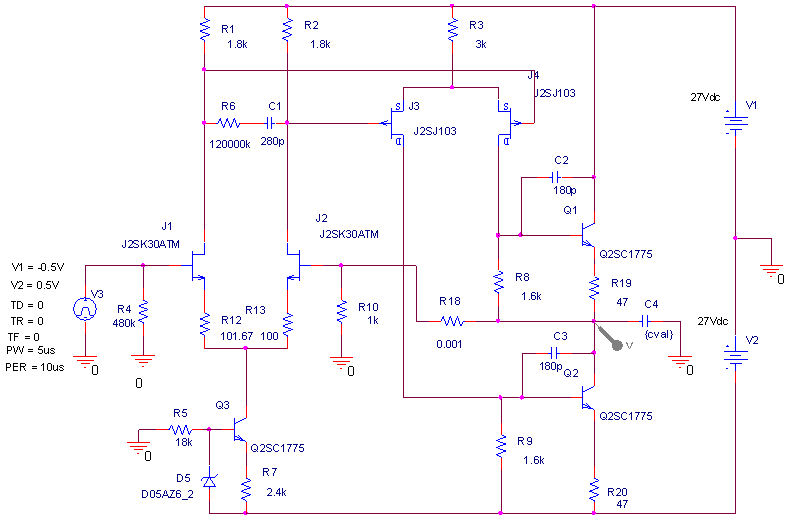
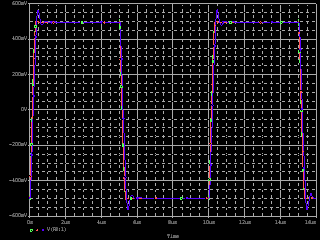
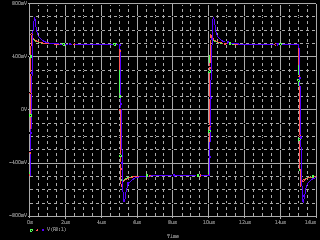
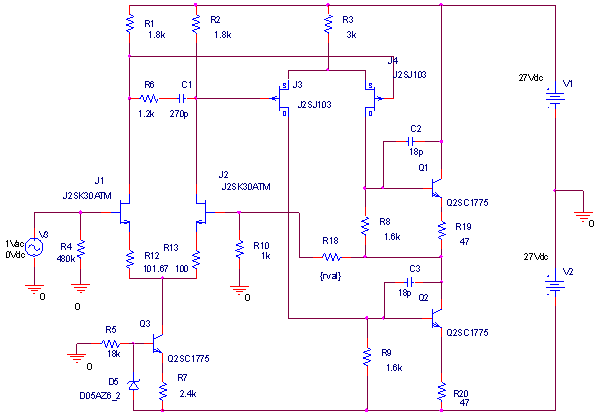
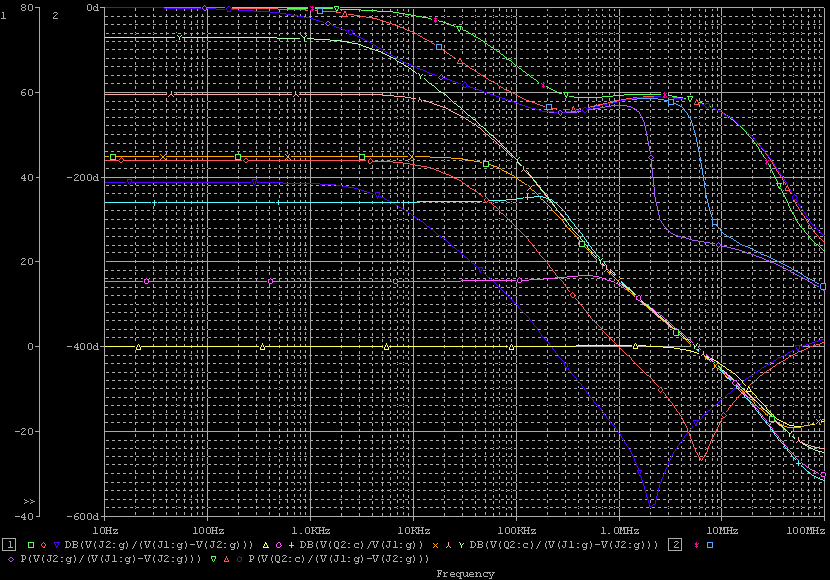
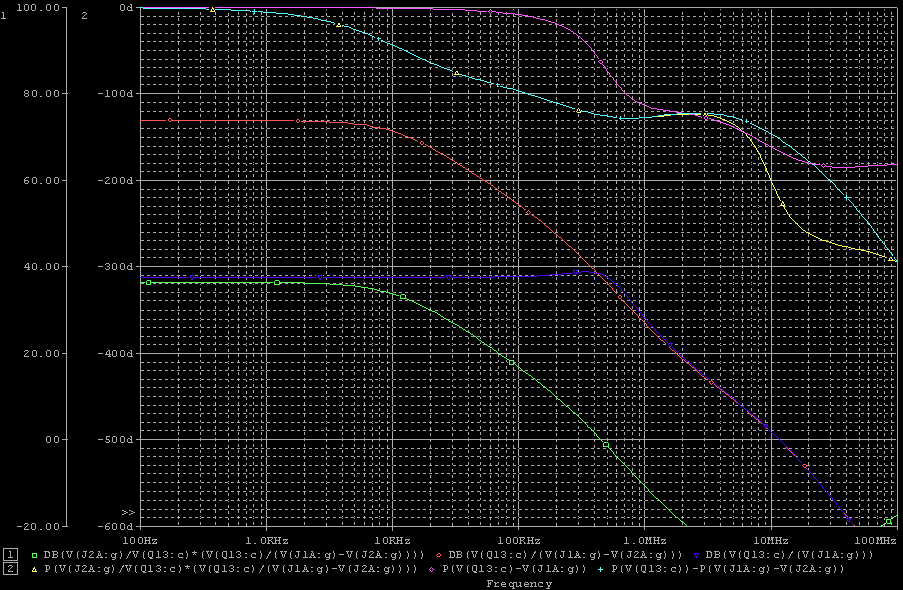
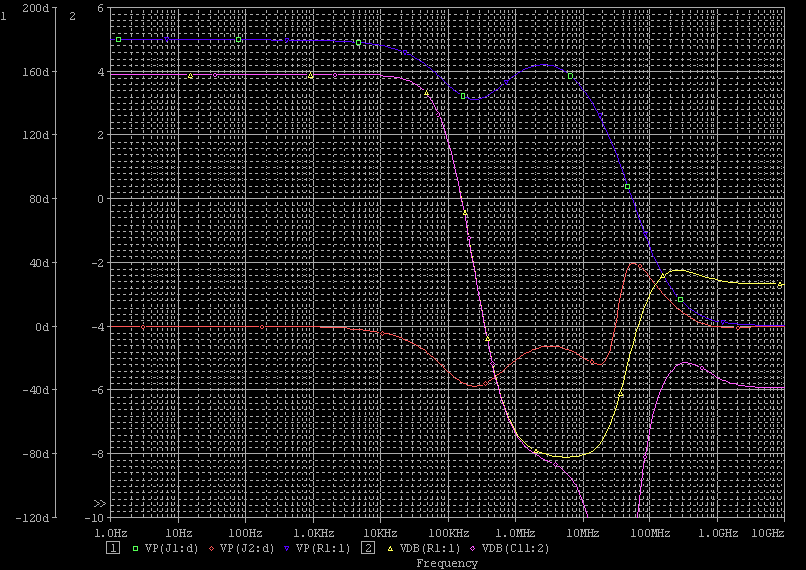
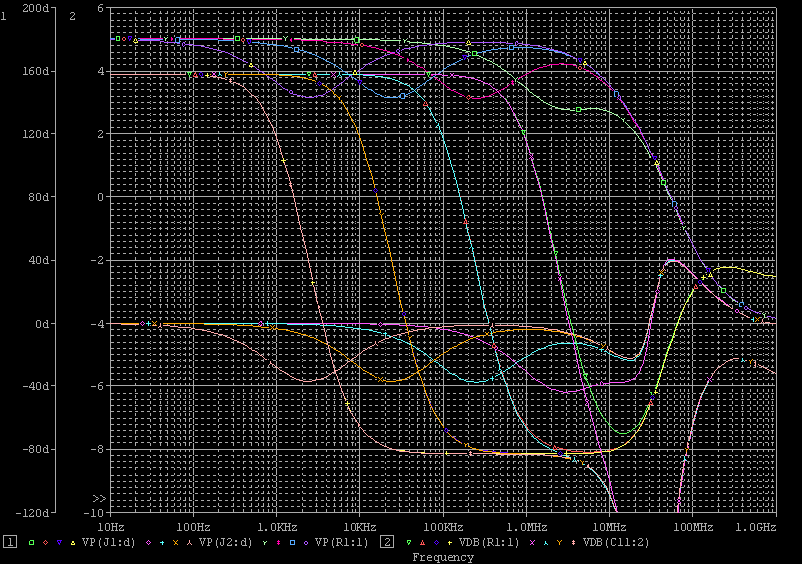
・ｆｃ１＝１／（２π＊（Ｒ１＋Ｒ２＋Ｒ３）＊Ｃ１１） 　　 ≒１５９／（（１．８＋１．８＋１．２）＊０．０００２７）=１２２．６８５ｋＨｚ ・ｆｃ２＝１／（２π＊Ｒ３＊Ｃ１１） 　　 ≒１５９／（１．２＊０．０００２７）＝４９０．７４１ｋＨｚ ・ｆｃｃ＝step中心周波数＝√ｆｃ１＊√ｆｃ２＝２４５．２３ｋＨｚ ・ｓｔｅｐ＝１．２／（１．８＋１．８＋１．２）＝０．２５≒▲１２．０４ｄＢ ・ｆｃ１はステップ低域側周波数であり、いわゆるＣＲローパスフィルタのカットオフ周波数のことなので、この周波数で利得がその周波数以下の利得に対して３ｄＢ低下し位相は４５°遅れ、これ以上の周波数では２０ｄＢ／decで利得が低下し、位相は最大９０°まで回転する。 ・ｆｃ２はステップ高域側周波数であり、いわゆるＣRハイパスフィルタのカットオフ周波数のことなので、この周波数で利得がその周波数以上の利得に対して３ｄＢ低下し位相は４５°遅れ、これ以下の周波数では２０ｄＢ／decで利得が低下し、位相は最大９０°まで回転する。 ・という二つのフィルタを組み合わせたのがステップ型位相補正。ちなみにその効果で区分してｆｃ１の方をポールと言いｆｃ２の方はゼロと言う。らしい。 ・結果、低域側ｆｃ１＝１２３ｋＨｚにおいて利得が−３ｄＢ、位相は−４５°回転し、それ以上の周波数では−２０ｄＢ／ｄｅｃで利得低下し位相も−９０°まで回転しようとするところ、すぐ近くの４９１ｋＨｚにステップ高域側のｆｃ２があって、この周波数でこれ以上の周波数に対して利得が−３ｄＢ、位相が−４５°になるように働くために、、位相回転はステップ中心周波数２４５ｋＨｚを谷の頂点として戻り回転に転じ、４９１ｋＨｚのｆｃ２の１０倍の４．９ＭＨｚでは位相遅れ０°まで回復する。他方、利得はステップ設定のとおり１２ｄＢ低下する。 ・となるはずだが、結果は下のグラフ。 ・一番上の青がＪ１ドレイン側電圧の位相、一番下赤がＪ２ドレイン側の位相で、当然１８０°違うのだがステップ位相補正の効果は同じだ。ｆｃ１，ｆｃ２で位相が−４５°まで回転していないが、この場合ｆｃ１，ｆｃ２が近く、相互に反作用として働くためだ。また、高域側で理論どおり回復していないが、これは１ＭＨｚ以上でＦＥＴ等の素子の高域限界による利得低下が始まってしまうからだろう。 ・真ん中にピンクと黄の線が重なっているのがＪ１、Ｊ２ドレインにおける電圧利得。ステップ位相補正の効果でｆｃ１の１／１０の１２ｋＨｚ付近から利得が低下し始め、ｆｃ２の１０倍の５ＭＨｚ付近でステップで設定したとおり１２ｄＢゲインが低下して減衰は終了している。それ以上の周波数でさらに減衰するのは、これもＦＥＴ等の素子自体の高域限界によるもの。 ・と、まぁ、大体そうなっているようだから、こんなところが当たらずとも遠からず。
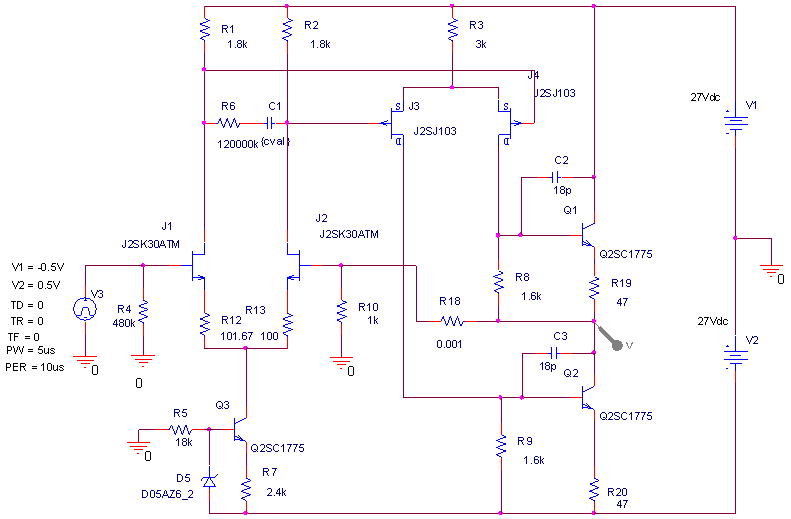
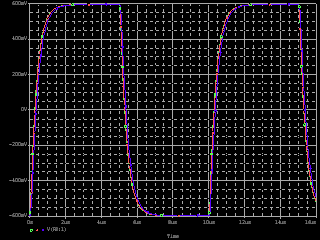
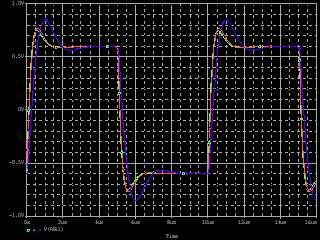
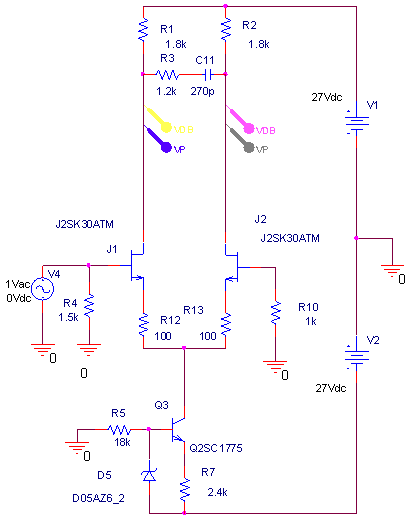
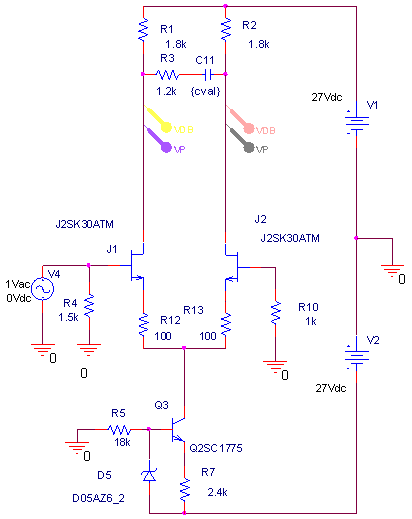
・何故、こうなるのか？ ・それは、ｆｃ１以下の周波数では実質Ｃ１１が絶縁と同じであるので、Ｊ１、Ｊ２の負荷がＲ１、Ｒ２であるのに対して、ｆｃ２以上の周波数では実質Ｃ１１が短絡と同じであるため、Ｊ１、Ｊ２の負荷がＲ３になるため。 ・ｆｃ１付近ではＣ１１の充電のためにＲ１、Ｒ２両端の電圧位相が遅れるのだが、ｆｃ２付近では同じくＣ１１の充電のためにＲ３両端の電圧位相が進む。 ・この組合せ。がステップ位相補正の構造、効果。 ・ステップ位相補正容量Ｃ１１を２７ｐＦ、２７０ｐＦ、２７００ｐＦ、２７０００ｐＦと２０ｄＢステップにパラメトリック解析すると、このステップ位相補正の構造、効果をより明確に観じることができる。 ・ｆｃ１、ｆｃ２の計算式から、単純に周波数が１０倍ずつずれた相似形になるものと予想されるが、どうか。 ・結果が下のグラフ。 ・説明を要しないほど分かりやすい結果になっている。 ・左から順にＣ１１＝２７０００ｐＦ、２７００ｐＦ、２７０ｐＦ、２７ｐＦの場合。 ・１ＭＨｚ以上で理論どおりにならないのは、ｆＴ等の素子の高域限界が現れるから。 ・余計なことだが、この例でも分かるように１ＭＨｚ以上はもう素子の高域限界による訳の分からないポール等が有象無象の魑魅魍魎な世界であるようだ。だから、これを何とかしようなどと大それたことを考えても徒労に終わる確率が高いので、これ以上の周波数領域は切り捨てる（＝ループゲインが０ｄＢに沈むポイントを１ＭＨｚ程度に設定する）のがアマチュアたるもののアンプ作りでは大事なたしなみである。 ・だから、そうすると必然的に、ループゲインが２０ｄＢならファーストポールは１００ｋＨｚ以下、同じく４０ｄＢなら１０ｋＨｚ以下、６０ｄＢなら１ｋＨｚ以下、８０ｄＢなら１００Ｈｚ以下、１００ｄＢなら１０Ｈｚ以下というポール配置になる訳で、K式も基本的にそうなっている。 ・が、そうは言ってももろもろの事情でそう出来ない場合もある訳で、ある程度何とか出来る範囲内であればこれを位相補正の手法で何とかする。ということになる。 ・で、その一つの手法が初段ステップ位相補正。
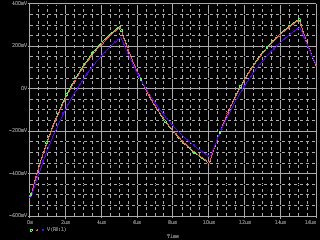
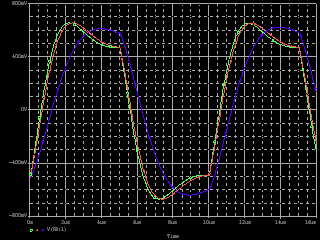
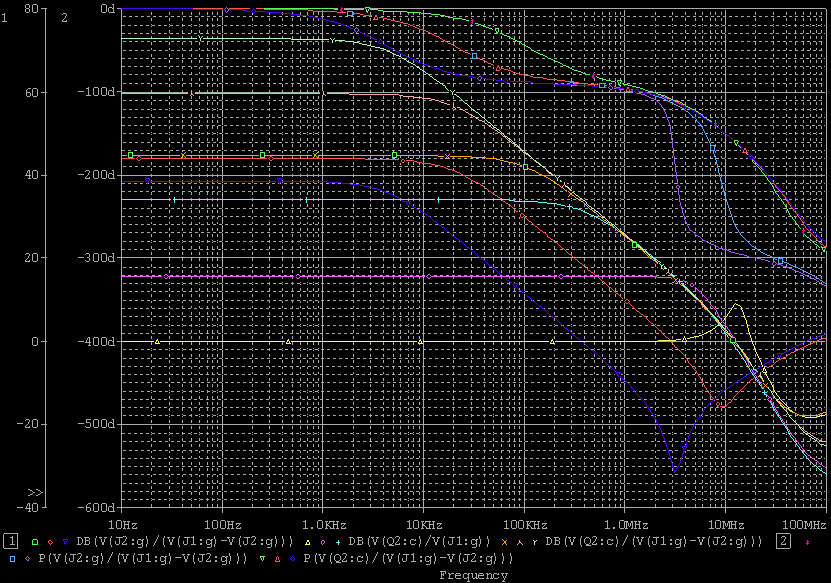
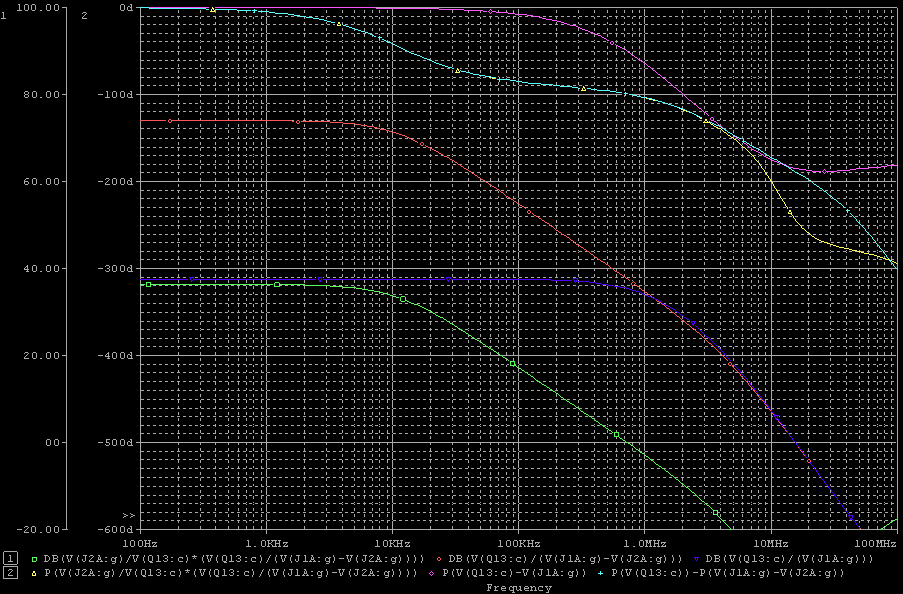
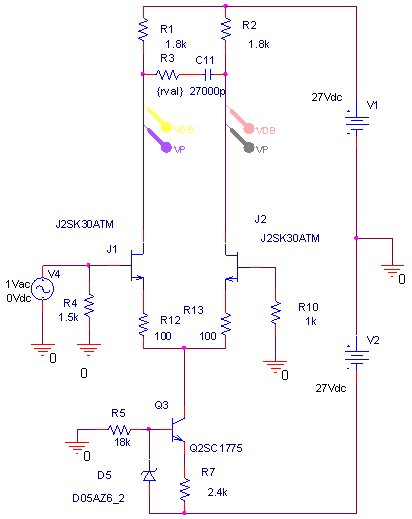
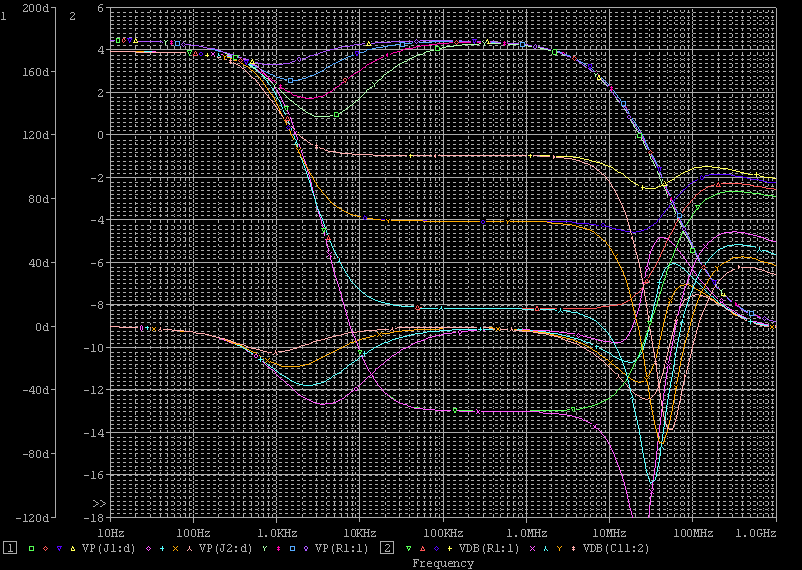
・次に、Ｒ３を６００Ω、１．２ｋΩ、２．４ｋΩ、４．８ｋΩと６ｄＢステップで増加させた場合のステップ位相補正の効果をパラメトリック解析で観る。 ・C11は２７０００ｐFと大きく設定した。のは、ステップ位相補正の効果を純粋に観るために素子の高域限界の影響が出ない領域に設定するため。C11を１０分の１、１００分の１とした場合は、それぞれ周波数が10倍、１００倍の領域で相似な効果が現れるだけ。なのは上のシミュレーションから明らか。 ・で、 ・R３=６００Ωの場合、 ・ｆｃ１＝１５９／（４．２＊０．０２７）＝１．４０２ｋＨｚ ・ｆｃ２＝１５９／（０．６＊０．０２７）＝９．８１５ｋＨｚ ・fcc＝√１．４０２＊√９．８１５＝３．７０９ｋＨｚ ・step＝０．６／４．２＝０．１４３＝▲１６．９ｄB ・R3=1.2kΩの場合は、 ・ｆｃ１＝１５９／（４．８＊０．０２７）＝１．２２７ｋＨｚ ・ｆｃ２＝１５９／（１．２＊０．０２７）＝４．９０７ｋＨｚ ・fcc＝√１．２２７＊√４．９０７＝２．４５４ｋＨｚ ・step＝１．２／４．８＝０．２７５７＝▲１０．９ｄB ・R3=２.４kΩの場合は、 ・ｆｃ１＝１５９／（６＊０．０２７）＝０．９８１ｋＨｚ ・ｆｃ２＝１５９／（２．４＊０．０２７）＝２．４５４ｋＨｚ ・fcc＝√０．９８１＊√２．４５４＝１．５５２ｋＨｚ ・step＝２．４／６＝０．４＝▲８．０ｄB ・R3=４.８kΩの場合は、 ・ｆｃ１＝１５９／（８．４＊０．０２７）＝０．７０１ｋＨｚ ・ｆｃ２＝１５９／（４．８＊０．０２７）＝１．２２７ｋＨｚ ・fcc＝√０．９８１＊√２．４５４＝０．９７２ｋＨｚ ・step＝４．８／８．４＝０．５７１＝▲４．９ｄB ・と計算されるが、シミュレーション結果は下のグラフ。 ・一番上の１ｋHzあたりから１０ｋHzあたりでくぼんでいるのがＪ１ドレイン側電圧の位相で、R3=６００Ωの場合が緑、１．２ｋΩの場合が赤、２．４ｋΩの場合が青、４．８ｋΩの場合が紫だ。一番下の位相が１８０°ずれて同様にくぼんでいるのがＪ２ドレイン側の位相で、R3＝６００Ωの場合がピンク、１．２ｋΩの場合が水色、２．４ｋΩの場合が橙、４．８ｋΩの場合がうすピンクだ。ステップ中心周波数まで位相が遅れ、中心周波数から位相が戻る様子が良く分かるし、それぞれ計算とよく一致している。また、R3が小さい方が位相の遅れ＆戻りのくぼみが深くかつ広くなることもよく分かる。 ・この2種のグラフの間にあって2本づつ重なっている4つのグラフがＪ１、Ｊ２ドレインにおける電圧利得で、下からR3が６００Ω、１．２ｋΩ、２．４ｋΩ、４．８ｋΩの場合だが、それぞれの減衰量も計算どおり。

・この初段ステップ位相補正の効能の実際をＮｏ−１６８ＣＤラインアンプで観じる。 ・そのために、わざとＮｏ−１６８ＣＤラインアンプの初段のステップ位相補正素子を外して１００ｋＨｚ方形波を入力し、その出力応答波形から１ＭＨｚ超領域と思しき利得交点周波数付近における位相回転の様子を観じる。
Ｖ−Ｌｅｖｅｌ　１（１ｋΩ）	Ｖ−Ｌｅｖｅｌ　１．５（１．５ｋΩ）	Ｖ−Ｌｅｖｅｌ　２（２ｋΩ）
・まずはボリューム位置が１の状態。この場合帰還抵抗値は１ｋΩ程度となるのでアンプのクローズドゲインは２倍（６ｄＢ）の状態だ。 ・発振している。発振周波数は６ＭＨｚ程度のようだ。	・次がボリューム位置が１．５の状態。帰還抵抗値は大体１．５ｋΩ。クローズドゲインは２．５倍（8dB）。 ・弱まって収束傾向だが、やはり５MHｚ程度の発振波形が乗っている。クローズドゲイン設定を増加させると利得交点周波数は低域に移行し、これに伴い発振周波数もやや下がったのだ。	・次がボリューム位置が２の状態。帰還抵抗値は大体２ｋΩ。よってクローズドゲインは３倍（９．５dB）。 ・発振は止まったように見える。が、肩部分に発振波形が残っている。収束しているように観じられるが、そうだとしてもリンギングの周波数が高めなので、この場合はもう少し位相余裕を取りたい。
Ｖ−Ｌｅｖｅｌ　３（３．５ｋΩ）	Ｖ−Ｌｅｖｅｌ　５（９ｋΩ）	Ｖ−Ｌｅｖｅｌ　７（２２ｋΩ）
・次にボリューム位置が３の状態。帰還抵抗値は大体３．５ｋΩ。よってクローズドゲインは４．５倍（１３dB）。 ・まだ、肩部分に２MHｚの発振波形の痕跡が残っているが、まぁ、これなら良好の範囲として良いかな。	・次にボリューム位置が５の状態。帰還抵抗値は大体９ｋΩ。よってクローズドゲインは１０倍（２０dB）。 ・完全に良好な応答波形。	・次にボリューム位置が７の状態。帰還抵抗値は大体２２ｋΩ。よってクローズドゲインは２３倍（２７dB）。 ・完全に良好な応答波形。
Ｖ−Ｌｅｖｅｌ　１０（５０ｋΩ）
・最後にボリューム位置が１０（最大）の状態。帰還抵抗値は５０ｋΩ。よってクローズドゲインは５１倍（３４dB）。 ・完全に良好な応答波形。
・このように、私の製作したＮｏ−１６８ＣＤラインアンプは、初段のステップ位相補正がない場合、ボリュームが回転角目盛りの１．５以下では明らかに発振し、逆にボリュームが回転角目盛り２以上であれば発振しないことが分かる。ただし、発振の痕跡もない完全良好な状態はボリューム４〜５以上である。 ・したがって、余計なことだが、Ｎｏ−１６８ＣＤラインアンプは昔のＧＯＡ時代のＶＧＡプリのようにＮＦＢ帰還回路に帰還制限抵抗として２ｋΩ以上を入れておけば、初段ステップ位相補正なしでも安定して動作するだろう。 ・すなわち、Ｎｏ−１６８ＣＤラインアンプの初段位相補正の役割は、ボリュームが回転角目盛りの２以下での位相余裕の確保である。ということになる。 ・何故なら、Ｎｏ−１６８のファーストポールは終段２ＳＣ９６０（ｏｒ９５９）のＣｏｂによるものなので、終段の電圧ゲインに伴ってミラー効果でＣｏｂが実質増大し、その結果ファーストポールはより低周波方向に移動するという構造で、アンプ負荷増大に伴うオープンゲインの増大があってもＮＦＢ安定性は基本的に確保される構造だからだ。結局、Ｎｏ−１６８においては、ボリュームを小さくするほどにファーストポールが高くなり、１ＭHｚ超領域のもろもろのポールとの距離が近づき、そのオープンゲインから必要となる所要のスタガー比が確保出来なくなって発振するという因果律である。 ・だから、外部位相補正をしない状態のＮｏ−１６８は、ボリューム最小状態に近づくにつれて発振し易い。だから、逆にもしボリューム最小でもスタガー比が確保できて安定に動作するならば、その場合はＮｏ−１６８は全く外部位相補正を要しない。のであるが、この場合はそうはなっておらず、ボリューム最小に近づくにつれ、ループゲインが０ｄＢに沈むポイントが１ＭHｚ〜１０ＭＨｚと上昇し、その地点ではセカンド以降のポールの影響で位相回転が１２０°を超えて回転を早める状況となり、結果、発振しているのだ。 ・というように、この方形波応答結果から観じられる。

・そのあたりをシミュレーションで観じる。そのための回路は下の通り。 ・まずは、ステップ位相補正がないのと同等の状態にするため、初段のステップ位相補正のＲ６を極大にし、観る。終段は２ＳＣ１７７５のモデルのＢ−Ｃ間に１８ｐＦのコンデンサーをＣｏｂ代わりにつないで２ＳＣ９６０相当にする。帰還抵抗であるＲ１８を０．００５Ω（要するに０Ω）、５ｋΩ、５０ｋΩと変化させるパラメトリック解析でその場合のオープンゲイン、ループゲイン、クローズドゲインの量とそれらの位相を観る。

・その結果がこれだが、まず見方。 ・グラフの一番上のグループがオープンゲインとループゲインの「位相」のグループで、この場合両者はほとんど重なっているのだが、一番上の緑がＲ１８＝０Ωの場合、赤がＲ１８＝５ｋΩの場合、青がＲ１８＝５０ｋΩの場合である。その縦軸は左の２の方で単位は度（°）である。オープンゲインの位相とループゲインの位相は１ＭＨｚ超の領域で多少様相が変わる。１ＭＨｚ超の領域におけるオープンゲインの位相はグラフの一番上でなだらかに低下している部分に線が重なってるが、ループゲインの位相の方はＲ１８＝０Ωの場合はこの線に重なっているが、Ｒ１８＝５ｋΩの場合はその下の水色の線であり、Ｒ１８＝５０ｋΩの場合はさらにその下の紫の線である。要するにループゲインの位相回転がＲ１８の増とともに急激に大きくなっているのだ。なぜこうなるのか？不明（＾＾； ・他は「利得」なので縦軸は左の１の方で単位はｄＢなのだが、一番上から３つがオープンゲインであり、上からＲ１８が５０ｋΩ（低域で７２．５ｄＢ）、５ｋΩ（６０ｄＢ）、０Ω（４４．５ｄＢ）の場合である。つぎの３つがループゲインであり、こちらは上からＲ１８が０Ω（４４．５ｄＢ）、５ｋΩ（４４ｄＢ）、５０ｋΩ（３８ｄＢ）の場合である。うち０Ωの場合のループゲインの線とオープンゲインの線は完全に重なっている。（グラフでは４４．５ｄＢのところにあるオレンジの線だが、よく見るとこれは線が２本重なっていることが分かる。）Ｒ＝０Ωの場合、帰還率β＝１であるから、まぁ、当然こうならないとおかしい。そして下の３本がクローズドゲインであり、上からＲ１８が５０ｋΩ（３４ｄＢ）、５ｋΩ（１６ｄＢ）、０Ω（０ｄＢ）の場合である。 ・これにより、Ｎｏ−１６８のオープンゲインは負荷が１ｋΩの場合低域で４４．５ｄＢ、その場合のオープンゲインの高域カットオフ周波数ｆｃは１００ｋＨｚであり、同様に負荷６ｋΩでは６０ｄＢ、２０ｋＨｚ、負荷５１ｋΩでは７２．５ｄＢ、４．５ｋＨｚである。ループゲインは、このアンプがＮＦＢ前はトランスコンダクタンス（電流出力）なので、オープンゲインとクローズドゲイン設定に関わらず理論的には一定であるが、この世では理想と現実の間には必ず乖離が生じるので、この場合も負荷１ｋΩで４４．５ｄＢ、負荷６ｋΩで４４ｄＢ、負荷５１ｋΩでは３８．５ｄＢとなっている。 ・クローズドゲインは所要のＮＦＢが確保されているので、負荷５１ｋΩの場合３４ｄＢ、６ｋΩの場合１６ｄＢ、１ｋΩの場合０ｄＢと理論どおりである。が、もちろん理論通りなのは低域においてであり、高域ではｆＴ等の素子の高域限界によりゲインは低下する。

・で、ループゲインが１倍＝０ｄＢ以上の時にループゲインの位相が１８０°回転してしまうと負帰還が正帰還になって発振してしまう。ので余裕をみて１２０°以内に設定するのが吉とされている。 ・この場合、負荷５１ｋΩ（ボリューム最大）ではループゲインが０ｄＢに沈むポイントは４００ｋＨｚで、そのポイントにおけるループゲインの位相回転は９０°であるので、この場合アンプは全く安定であろうことが分かる。その証としてクローズドゲインには何のピークも生じていない。同様に負荷５ｋΩ（５０ｋΩのボリュームで１１時付近）の場合、ループゲインが０ｄＢに沈むポイントは３ＭＨｚで、そのポイントにおけるループゲインの位相回転は１１０°であるので、この場合もアンプは全く安定であろうことが分かる。したがってこの場合もクローズドゲインには何のピークも生じていない。が、負荷１ｋΩ（ボリューム最小）の場合はループゲインが０ｄＢに沈むポイントが１０ＭＨｚ超となり、そのポイントにおけるループゲインの位相回転は１６０°であるので、この場合アンプは発振に至らずとも不安定であろうことが分かる。その証としてクローズドゲインには１０ＭＨｚ超のポイントで１０ｄＢ程度のピークが生じている。

・これが方形波応答ではどう現れるかを観る。
Ｒ１８＝０Ω、よって負荷１ｋΩの場合	Ｒ１８＝５ｋΩ、よって負荷６ｋΩの場合	Ｒ１８＝５０ｋΩ、よって負荷５１ｋΩの場合
・この場合、やはりリンギングが生じている。収束しているから発振状態とはいえないが、リンギングは発振の入り口であり安定な状況とは言えない。上のグラフでループゲインが０ｄＢに沈むポイント＝１１ＭＨｚにおけるその位相は１６０°に達していることから、位相余裕はほとんどなく、状況によっては完全な発振状態に至るだろう。	・この場合、クローズドゲインの高域カットオフ周波数は４〜５ＭＨｚであるので、１００ｋＨｚ方形波は丸くなることなくきれいに通る。立ち上がり立ち下がりでオーバーシュートが１波生じている。これは上のグラフの通りクローズドゲインにピークは生じていないものの、３ＭＨｚ〜１０ＭＨｚにおいてクローズドゲインがオープンゲインをやや上回っている＝この部分でやや正帰還になっていることによるものだろう。	・この場合、クローズドゲインの高域カットオフ周波数が１００ｋＨｚ以下であることから立ち上がり立ち下がりの肩特性は丸くなっているが、応答としては極めて素直だ。
・このシミュレーション結果は、私の製作したＮｏ−１６８ＣＤラインアンプにおける実際の方形波応答に良く似ている。 ・が、実機の方はＲ１８＝０Ω程度に低い場合はもっとリンギングが激しいし、Ｒ１８＝５ｋΩ程度の場合にはリンギングの現れ方もシミュレーションと実機の場合で少し違う。 ・この辺愚考するに、まず後者についてだが、これは実機の方における発振器の性能が良くない、要するに発振器の発振方形波の肩がなまっているということに尽きるように思われる。実際シミュレーションのように立ち上がり時間０で無限に立ち上がれる信号をこの世で現実に作ることは出来ないので、これはしょうがない。シミュレーションのこの状態は、実機の方では肩部分でのギザギザとして現れていると思われる。 ・次に前者の方だが、これは一つにはシミュレーションでは無視している浮遊容量等の影響だろう。例えばアンプ負荷につながる見えない容量負荷もある。２４９７を３ｍも伸ばせばそれだけでも２００ｐＦぐらいの容量負荷がつながるが、そうでなくとも実機ではどこにステルス容量があって位相回転を助長しているか分からない。ので、この考え方の妥当性を検証するために負荷に２００ｐＦの容量をつないでシミュレーションしてみる。

Ｒ１８＝０Ω、よって負荷１ｋΩの場合	Ｒ１８＝５ｋΩ、よって負荷６ｋΩの場合	Ｒ１８＝５０ｋΩ、よって負荷５１ｋΩの場合
・ま、必ずしも同じではない。が、このシミュレーション結果と実機での実際の応答は、定量的にはやや相違があるものの定性的には良く相応しており、考え方も概ね正しいらしいとは言えるだろう。

・さて、このボリューム０Ω付近（＝アンプ負荷が１ｋΩ〜３ｋΩ程度の状態であるとき）において不安定or発振してしまう状態を改善し、Ｎｏ−１６８のボリュームを０Ω〜５０ｋΩまで変化させても安定に動作させるための位相補正手法が初段のステップ位相補正。 ・なのだが、その前に別の位相補正もやってみる。Ｎｏ−１６８ＣＤラインアンプの第１ポールを発生させているのは終段２ＳＣ９５９（９６０）のＣｏｂであるので、このシミュレーションでそのＣｏｂ相当で２ＳＣ１７７５のベース−コレクタ間につないだＣ２、Ｃ３の容量を増やす（実機であれば２ＳＣ９５９（９６０）のＢ−Ｃ間にＣを外付けする）ことにより位相補正を行い、そのポールの周波数を引き下げ所要のスタガー比を確保するという、要するに基本的な位相補正手法である。 ・という訳で、C2、C3を１８０ｐFに増やしてシミュレート。

・結果、位相補正効果により、オープンゲインのｆｃ（＝要するに第１ポール）が１２ｋＨｚから６５０Ｈｚ程度と、位相補正前の１００ｋＨｚから４．５ｋＨｚの１０分の１程度まで下に下がった。位相補正量が１０倍近くになったのでポールの周波数が１／１０近く低下したのだ。 ・これに伴ってループゲインが０ｄＢに沈むポイントもそれぞれより低い周波数に移行するが、ループゲインの位相回転状況は大きく変わらないため、これによって、負荷がどの場合でもループゲインの回転が１２０°に達する前にループゲインが０ｄＢに沈むことになった。ので、クローズドゲインには負荷１ｋΩの場合でも全くピークがなくなった。これならアンプの動作は全く安定になる。 ・これが位相補正の効能。

・その辺をシミュレーションの方形波応答で観る。Ｃ２、Ｃ３は１８０ｐＦだ。 ・また、この際、負荷にＣ４をつなぎ、これを０ｐＦ、２００ｐＦ、２０００ｐＦと変化させるパラメトリック解析で、容量負荷による影響とその場合の安定度も併せて観る。
Ｒ１８＝０Ω、よって負荷１ｋΩの場合	Ｒ１８＝５ｋΩ、よって負荷６ｋΩの場合	Ｒ１８＝５０ｋΩ、よって負荷５１ｋΩの場合
・ちょっと見にくいが、どの場合も緑がＣ４＝０ｐＦ、赤がＣ４＝２００ｐＦ、青がＣ４＝２０００ｐＦの場合。Ｒ１８＝０Ω、すなわち負荷１ｋΩの場合の方形波応答にちょっとオーバーシュートがあり、出力に付加される容量値が増加するほどにそれが大きくなることが分かるが、それでもこの程度なら安定動作の範囲だ。また、それ以外はどの場合も安定動作を示す方形波応答である。位相補正が上手く機能したと言えるだろう。 ・が、Ｒ１８＝５０ｋΩ（負荷５１ｋΩの場合）の方形波が完全に三角波となってしまっているように、どの場合も方形波の肩がなまっている。のは、オープンゲインのｆｃの低下とともにクローズドゲインのｆｃも一桁近く低域に下がってしまったからだ。要するに、この位相補正によりアンプの仕上がり高域特性が劣化し、アンプが低速になったのである。まぁ、位相補償とはもともとそういうものだ。 ・ので、この結果に満足できない場合は、別の位相補正手法を考えなければならない。

・そこで、初段ステップ位相補正。 ・結論が早いのでまず方形波応答から観る。
Ｒ１８＝０Ω、よって負荷１ｋΩの場合	Ｒ１８＝５ｋΩ、よって負荷６ｋΩの場合	Ｒ１８＝５０ｋΩ、よって負荷５１ｋΩの場合
・それぞれ１波で収束するオーバーシュートが生じているものの、リンギングとはなっていないので安定な動作を示す方形波応答だ。 ・かつ、上の終段のＢ−Ｃ間のＣで位相補正した場合に比較すると明らかにこちらの方が方形波の立ち上がり立ち下がりが鋭く、クローズドゲインの周波数がより高域まで伸びた高速な動作をしていることが分かる。 ・これが初段ステップ位相補正を採用する意義だろう。 ・ところで、このステップ位相補正を講じた実機における方形波応答が下の写真だが、シミュレーションが示すものと大変良く似ている。

・どうしてこうなるのか？を初段ステップ位相補正を利かせた場合のシミュレーションで観る。
・ステップ位相補正の効果の計算値はこう。 　・ｆｃ１＝１／（２π＊（Ｒ１＋Ｒ２＋Ｒ３）＊Ｃ１１）≒１５９／（（１．８＋１．８＋１．２）＊０．０００２７）=１２２．６８５ｋＨｚ 　・ｆｃ２＝１／（２π＊Ｒ３＊Ｃ１１）≒１５９／（１．２＊０．０００２７）＝４９０．７４１ｋＨｚ 　・step中心周波数＝√ｆｃ１＊√ｆｃ２＝２４５．２３ｋＨｚ 　・ｓｔｅｐ＝１．２／（１．８＋１．８＋１．２）＝０．２５≒▲１２．０４ｄＢ ・結果は下のグラフ。果たして計算値どおりだろうか。
・下のステップ位相補正がない場合と比較すると分かりやすい。 ・ステップ位相補正による中心周波数＝２４５ｋＨｚを中心として、オープンゲイン及びループゲインの位相が、それ以下の周波数では位相回転を速めている。ｆｃ１のポール（ステップ低域側周波数）が１２３ｋＨｚだから、１オクターブ下の１．３ｋＨｚ付近から下の場合に比べて回転が速まっているはずだが、確かにそうなっている。ステップ中心周波数以上の周波数ではｆｃ２のゼロ（ステップ高域側周波数）の４９１ｋＨｚの効果で、ステップ中心周波数からゼロの１０倍の周波数である４〜５MHｚまで位相を戻す効果が生じ、位相回転が引き戻されるはずだが、上下のグラフを比較してみると確かにそうなっている。が、高域側の位相戻し効果にも限界があって、Ｒ１８＝５ｋΩの場合と５０ｋΩの場合のループゲインの位相についてみると明らかなように、１ＭＨｚ超の領域での効果はかなり微妙な程度だ。この領域はｆｔ等の素子の高域限界の領域であり、それを何とかするのはかなり困難であることがこのことでも分かる。 ・ｓｔｅｐ＝１．２／（１．８＋１．８＋１．２）＝０．２５≒▲１２．０４ｄＢ効果については、この場合ステップ中心周波数でステップ位相補正がない場合に対してオープンゲインが▲６ｄB程度の低下、その１０倍の周波数２〜３MHｚで▲１２ｄB程度の低下となるはずだが、だいたいそうなっている。 ・で、このステップ位相補正の効果により、ループゲインが０ｄBに沈む周波数及びそのポイントにおけるループゲインの位相が、Ｒ１８＝０の場合４．５ＭＨｚ、−１１０°、Ｒ１８＝５ｋΩの場合１ＭＨｚ、−１１０°、Ｒ１８＝５０ｋΩの場合２１０ｋＨｚ、−１２２°となったこと、特にＲ１８＝０の場合（ボリューム最小位置の場合）に４．５ＭＨｚで位相回転が−１１０°と位相余裕が確保される状態になったことが肝だ。 ・合わせて、クローズドゲインの高域カットオフ周波数もステップ位相補正前に比べるとやや低下しているのだが、Ｒ１８＝５０ＫΩで３１０ｋＨｚ（４００ｋＨｚ）、Ｒ１８＝５ｋΩで１．３ＭＨｚ（４．５ＭＨｚ）、Ｒ１８＝０Ωで８ＭＨｚ（２０ＭＨｚ）となっている部分も肝である。
・すなわち、 ・この結果、ループゲイン及びクローズドゲインの周波数特性が最も高域に伸び、ステップ位相補正がない場合には発振してしまうＲ１８＝０（ボリューム最小）の場合についても安定にＮＦＢがかかる状態となり、Ｎｏ−１６８ＣＤラインアンプはボリュームが最小から最大までのどの状態でも安定に動作するようになったのである。 ・しかも、終段２ＳＣ９５９（９６０）のＢ−Ｃ間にＣを外付けする位相補正に比べると、ＮＦＢ後のクローズドゲインの高域カットオフ周波数は、Ｒ１８＝０Ωの場合、ステップ位相補正では８ＭＨｚであるのに対して終段位相補正では４ＭＨｚ、同様にＲ１８＝５ｋΩの場合では１．２ＭＨｚに対して４００ｋＨｚ、Ｒ＝５０ｋΩの場合では３００ｋＨｚに対して５０ｋＨｚと、ステップ位相補正では高域特性の劣化＝アンプの低速化の度合いを相対的に少なくできている。 ・初段ステップ位相補正、なかなかに上手い。
大体Ｒ１８＝０Ω、よって負荷１ｋΩの場合 （ステップ位相補正なし）	大体Ｒ１８＝５ｋΩ、よって負荷６ｋΩの場合 （ステップ位相補正なし）	Ｒ１８＝５０ｋΩ、よって負荷５１ｋΩの場合 （ステップ位相補正なし）
Ｒ１８＝０Ω、よって負荷１ｋΩの場合 （ステップ位相補正あり）	大体Ｒ１８＝５ｋΩ、よって負荷６ｋΩの場合 （ステップ位相補正あり）	Ｒ１８＝５０ｋΩ、よって負荷５１ｋΩの場合 （ステップ位相補正あり）
・と、ステップ位相補正によって、アンプの著しい低速化をもたらさずにＮｏ−１６８ＣＤラインアンプのＮＦＢ安定度を確保することが出来た訳だが、では、ステップ位相補正結果が完璧かというと、必ずしもそうではない。 ・それは、このステップ位相補正前と後の方形波応答写真で明らかであるし、シミュレーションでもこうなることが示されたのだが、Ｒ＝０Ωの場合は綺麗な方形波応答が得られるようになった代わりに、Ｒ＝５ｋΩの場合やＲ＝５０ｋΩの場合は方形波応答にオーバーシュートが付随することになってしまっていることだ。 ・その原因は上のシミュレーション結果から明らかで、ステップ位相補正で低域側に加わったポールの効果でステップ中心周波数まで位相回転が速まることにより、そのステップ中心周波数付近で位相回転が１２０°をやや超えてしまい、ちょうどそのあたりの周波数でＲ＝５ｋΩから５０ｋΩの場合のループゲインが０ｄＢに沈むのだが、その沈むポイントの前に位相回転が９０°を超え１２０°程度まで回ってしまうのでシミュレーション結果の通り、そのクローズドゲインにはやや盛り上がりが生じてしまうのである。すなわち、クローズドゲインがその周波数領域で大きくなってしまうため、方形波応答では当該周波数に当たる部分が写真のように盛り上がってオーバーシュートになってしまうのだ。 ・これを無くして、ボリューム位置がどこにあってもオーバーシュートやリンギングのない方形波応答が得られるように出来ないのだろうか？というとなかなか難しい。何故ならこれまでその構造を観てきたとこから分かるように、初段ステップ位相補正は、まだ余裕がある低域側の位相余裕を活用して高域側の位相余裕を確保する方式だからである。高域側の位相余裕を確保すると、同時に低域側の位相余裕は必ず減少してしまう。従って調整後の負荷５ｋΩや５０ｋΩの場合に現れる方形波のオーバーシュートは、ステップ位相補正に伴う副作用のようなものなのだ。だから、ステップ位相補正前のループゲインの位相回転の状況にもよるが、高域側で位相余裕を確保しすぎると低域側の位相余裕が無くなりボリュームを最大にした場合に発振したりする場合もありうるし、高域側、低域側両方、すなわちボリューム最小側と最大側でともに発振してしまうこともあり得る。この高域側と低域側のトレードオフを上手く調整して、負荷１ｋΩから５０ｋΩという広い範囲で安定なＮＦＢ状態を得ているのがＮｏ−１６８ＣＤラインアンプの初段ステップ位相補正。 ・これを、方形波応答の正確性＝アンプ動作の正確性という観点から見ると、このような結果をもたらすステップ位相補正は、Ｒ＝５ｋΩや５０ｋΩの場合の特性を犠牲にしてＲ＝０Ωの場合の安定度を確保したものだ。結局は妥協の産物又は次妻合わせの方策である。と評することも出来る。 ・が、この世においては理想は求めても得られないのが宿命だ。から、現実に対して最も適切な妥協又は辻褄合わせをするかが勘所であり肝要な対処法というものである。 ・そういう観点から考えると、ステップ高域側で持ち上げた位相余裕部分は、見えない浮遊容量や出力に繋がる容量等で常に余裕の減少の危険に晒されている部分であるから、可能な限り取り得る余裕は確保しておくべきなのであるのに対して、ステップ低域側で少なくなった位相余裕については、このような外部要因による更なる位相余裕の減少の危険性は少ない。したがって、ステップ位相補正の調整方針としては、ボリューム最大側での位相余裕よりボリューム最小側での位相余裕を優先確保するべきであるというところに当然帰結するから、高域側、低域側とも十分以上の位相余裕が得られないのであれば、低域側が発振してしまわない範囲で低域側の位相余裕を犠牲にしても高域側の位相余裕を確保すべなのである。 ・結局、Ｎｏ−１６８ＣＤラインアンプの初段１．２ｋΩ＋２７０ｐＦによるステップ位相補正により得られたこの方形波応答は、理想ではないが、極めて合理的な位相補正の証左である。とするのが妥当な結論だろう。

・さて、以上のように、初段ステップ位相補正は、まだ余裕がある低域側の位相余裕を活用して高域側の位相余裕を確保する方式であるので、これを採用すべきなのは、ループゲインが０ｄＢに沈む周波数が１ＭＨｚから１０ＭＨｚオーダーとなる動作をさせる場合、端的に言うと、現在のトランスコンダクタンス（電流出力）の完全対称型半導体式ＤＣプリ等では、帰還抵抗を小さくしてクローズドゲイン０ｄＢ付近で動作させる場合だ。ということになる。Ｎｏ−１９６の場合もそうだ。 ・そうではなく、帰還抵抗をある程度大きくし、クローズドゲインを１５ｄＢ（６倍）程度以上に設定する場合（この値は個体ごと異なる）は、この初段ステップ位相補正が不要であることは、上でみた一番最初の初段ステップ位相補正を取り去ったＮｏ−１６８ＣＤラインアンプの方形波応答写真からも明らかだし、以上の解析からも明らかだろう。そのような状況で同様の初段ステップ位相補正を付加すれば、良好な方形波応答をオーバーシュート付きの方形波応答にするだけでなく、位相補正によって動作スピードも低下させるし、素子の無駄でもある。 ・その意味で、我が“オーディオＤＣアンプ製作のすべて　下巻　半導体ＤＣマイク”については、とうの昔に初段ステップ位相補正を取り払ってしまっている。 ・が、オリジナルにはこの場合も初段ステップ位相補正が付いている。 ・ので、この“オーディオＤＣアンプ製作のすべて　下巻　半導体ＤＣマイク”のシミュレートなのだが、まずはオリジナル通りに初段ステップ位相補正を付加した場合。
・その結果がこれだが、上からピンクがクローズドゲインの位相、水色がオープンゲインの位相、低域で水色と重なっていて２ＭＨｚ以上で分離する黄色がループゲインの位相、赤がオープンゲイン、青がクローズドゲイン、そして緑がループゲインである。 ・オープンゲインとループゲインの位相のラインが７００ｋＨｚを底にして窪んだ形になっているが、勿論これがステップ中心周波数であり、ここから４〜５ＭＨｚの領域に向けて位相が戻っている。正にこれが初段ステップ位相補正の効果だが、このステップ中心周波数で位相回転が１３０°近くになっているのも同じくステップ位相補正の効果である。 ・そしてこの場合の半導体ＤＣマイクアンプのループゲインは４５０ｋＨｚで０ｄＢに沈んでいるのだが、このポイントにおいてループゲインの位相は、このステップ位相補正の効果で１２０°以上に回転してしまっており、その結果クローズドゲインのラインは２００ｋＨｚから４００ｋＨｚがやや盛り上がってしまっている。ということが明らかだ。
・その結果、下の方形波応答写真のとおり、１００ｋＨｚ方形波応答にはオーバーシュートが生じ、１０ｋＨｚ方形波応答ではこれがひげのようなオーバーシュートとなって現れているのである。
１００ｋＨｚ方形波応答（ステップ位相補正あり）	１０ｋＨｚ方形波応答（ステップ位相補正あり）
・初段ステップ位相補正の意義なり効果なりが分かれば、この場合は初段ステップ位相補正は不要だという考えに当然至る。ので、初段ステップ位相補正を取り払った場合をシミュレート。
・結果がこれだが、説明も要しない結果だろう。ステップ位相補正による低域側ポールによる位相回転がなくなったので、ループゲインが０ｄＢに沈むポイントが７００ｋＨｚと高域に伸びたが、そのポイントにおけるループゲインの位相回転も減り１００°にとどまっている。この結果、クローズドゲインには盛り上がりやピークは全くなくなった。
・その結果、下の方形波応答写真のとおり、１００ｋＨｚ方形波応答のオーバーシュートは消滅し、１０ｋＨｚ方形波応答でのひげのようなオーバーシュートも消滅している。 ・位相余裕が拡大し、より適切なＮＦＢがかかったことの証左だ。
１００ｋＨｚ方形波応答（ステップ位相補正なし）	１０ｋＨｚ方形波応答（ステップ位相補正なし）
・このように、クローズドゲイン３８ｄＢの固定ゲインで動作させる“オーディオＤＣアンプ製作のすべて　下巻　半導体ＤＣマイク”には初段ステップ位相補正は不要だ。 ・では、何故オリジナルではこの初段ステップ位相が付けられているのだろうか？ ・それは勿論分かろうはずもない。
・毎度のことだが最後にいつものお断り。 ・以上のシミュレーション結果及びその解析には何の保証もないので悪しからず。また、登場した素子モデルについては何もお答えできない。ので重ねて悪しからず。

２００８年１０月２８日