俹俽倫倝們倕乮昡壙斉乯偱俶倧亅侾俇俉傪僔儈儏儗乕僩偡傞
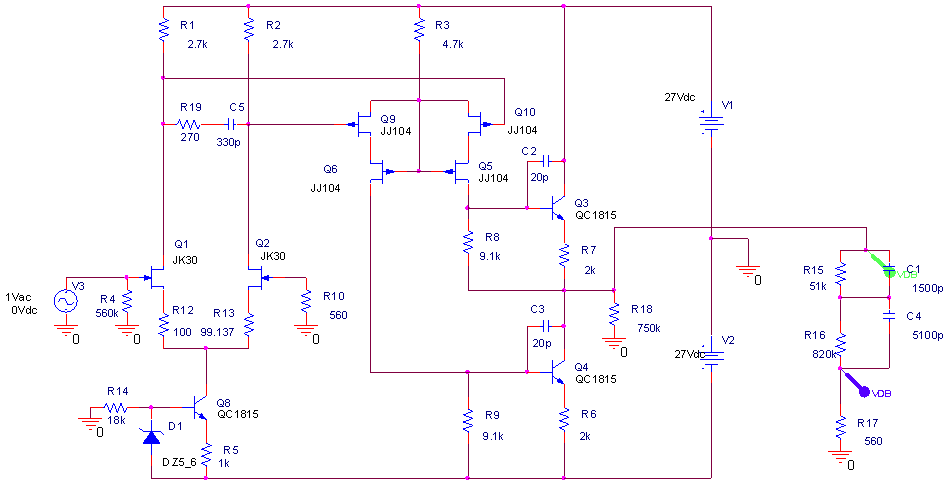
仜棟憐俶俥宆僀僐儔僀僓乕
棟憐俶俥宆僀僐儔僀僓乕偼丄揹棳弌椡傾儞僾亄俶俥宆僀僐儔僀僓乕偵傛偭偰幚尰偡傞丅
揹棳弌椡傾儞僾偺弌椡偵俼俬俙俙俶俥俛慺巕傪宷偖偲丄僆乕僾儞僎僀儞偺弌椡揹埑摿惈偑俼俬俙俙摿惈偦偺傕偺偵側傞丅
偙傟傪俼俬俙俙俶俥俛慺巕偱婣娨偡傞偲丄棟榑揑偵偼婣娨揹埑偺廃攇悢摿惈偼僼儔僢僩丄埵憡摿惈偼侽亱偺棟憐揑側俶俥俛偵側傞偺偱偁傞丅
僀僐儔僀僓乕傾儞僾偺弌椡偵俶俥俛慺巕傪宷偄偱傾儞僾弌椡揹埑偲俶俥俛婣娨揹埑偺棙摼偲埵憡偺廃攇悢摿惈傪娤傞丅
愭偢偼弌椡揹埑棙摼摿惈
忋偑傾儞僾偺弌椡揹埑丄壓偑婣娨揹埑偩丅
弌椡揹埑偼妋偐偵俼俬俙俙摿惈偵嬤偄傕偺偲側偭偰偄傞偑丄俀侽侽俫倸埲壓偺懷堟偲俀侽俲俫倸埲忋偺懷堟偱偼俼俬俙俙摿惈偐傜傗傗槰棧偟偰偄傞丅
掅堟偺槰棧偼傾儞僾偺弌椡僀儞僺乕僟儞僗偺尷奅丄崅堟偺槰棧偼傾儞僾偺崅堟摿惈偺尷奅偵傛傞傕偺偩丅
掅堟偵偮偄偰偼傕偆堦偮丄弌椡偵僷儔偵擖偭偰偄傞俈俆侽倠兌傕槰棧偺尨場偩偑丄偙傟偼師偵宷偑傞僼儔僢僩傾儞僾偺擖椡僎乕僩掞峈乮亖僼儔僢僩傾儞僾擖椡僀儞僺乕僟儞僗乯側偺偱偟傚偆偑側偄丅
寢壥丄婣娨揹埑偼俀侽侽俫倸偐傜俀侽倠俫倸傑偱偼傑偢傑偢棟憐偵嬤偄僼儔僢僩側摿惈偵側偭偰偄傞丅偲尵偊傞偩傠偆丅
俀侽侽俫倸埲壓偺掅堟偱婣娨揹埑偑嵟戝亅俉倓俛掅壓偟偰偄傞偑丄偙偺掱搙偱偁傞偲偙傟偼傾儞僾偺弌椡僀儞僺乕僟儞僗偲尵偆傛傝弌椡偵僷儔偵擖偭偰偄傞俈俆侽倠兌偑庡梫側梫場偩丅
師偵弌椡揹埑偺埵憡摿惈
偙偪傜偼忋偑婣娨揹埑偺埵憡丄壓偑弌椡揹埑偺埵憡偱偁傞丅
棟憐揑偵偼忋偺婣娨揹埑偺埵憡摿惈偑埵憡嵎侽亱偺捈慄偵側傞偙偲偩偑丄尰幚偵偼條乆側惂栺偐傜棟憐偐傜偼傗傗奜傟偰偟傑偆丅
偑丄侾侽俫倸偐傜俀侽俲俫倸傑偱埵憡嵎亇俁侽亱埲撪偵廂傑偭偰偍傝丄幚偵慺惏傜偟偄棟憐揑側摿惈偲尵偊傞偩傠偆丅
棟憐俶俥宆僀僐儔僀僓乕偺柺栚桇擛偲偄偭偨偲偙傠偩丅
揹棳弌椡傾儞僾偱偁傞俶倧亅侾俇俉僀僐儔僀僓乕偺弌椡偵擖椡僀儞僺乕僟儞僗偺掅偄婡婍傪宷偄偱偼偄偗側偄丅
弌椡偵侾俇俵兌丄俉俀侽倠兌丄係侽侽倠兌丄俀侽侽倠兌丄俆侽倠兌傪僷儔偵宷偄偱偦偺塭嬁偑偳偆側傞偐娤偰傒傛偆丅
愭偢偼弌椡揹埑棙摼摿惈偱摨偠偔忋偑傾儞僾偺弌椡揹埑丄壓偑婣娨揹埑偩偑丄
偳偪傜傕忋偐傜僷儔偵宷偄偩掞峈抣偑侾俇俵兌丄俉俀侽倠兌丄係侽侽倠兌丄俀侽侽倠兌丄俆侽倠兌偺応崌偩丅
傾儞僾偺弌椡揹埑棙摼摿惈偼丄傾儞僾弌椡偵僷儔偵宷偄偩掞峈抣偑彫偝偔側傞傎偳偵俼俬俙俙摿惈偐傜戝偒偔奜傟偰偟傑偆丅俆侽倠兌偺応崌偼侾侽倠俫倸埲壓偺掅堟偱偺棙摼偺惙傝忋偑傝偑懌傝偢嵟憗俼俬俙俙摿惈偲偼尵偊側偄偩傠偆丅
婣娨揹埑傕僷儔偺掞峈抣偑彫偝偔側傞傎偳偵掅堟偺槰棧偑峀斖偐偮戝偒側傕偺偲側偭偰偄傞丅僷儔掞峈俆侽倠兌偱偼婣娨揹埑偑僼儔僢僩側偺偼侾侽倠俫倸乣俀侽倠俫倸偺斖埻偖傜偄偱丄掅堟偱偼側傫偲侾侽俫倸偱亅俀係倓俛傕尭悐偟偰偟傑偭偰偄傞丅
側偍丄偙偺偄偢傟偺応崌偱傕懳墳偡傞僆乕僾儞僎僀儞棙摼偐傜婣娨揹埑傪堷偒嶼偡傞偲暘偐傞傛偆偵丄俶俥俛屻偺僋儘乕僘僪僎僀儞偽偳傟傕惓偟偔俼俬俙俙摿惈偵偼側傞偺偱偁傞丅
師偵弌椡揹埑偺埵憡摿惈
忋偑婣娨揹埑偺埵憡丄壓偑弌椡揹埑偺埵憡側偺偼忋偲摨偠偩偑丄偳偪傜傕忋偐傜僷儔偺掞峈偑俆侽倠兌丄俀侽侽倠兌丄係侽侽倠兌丄俉俀侽倠兌丄侾俇俵兌偺応崌偱偁傞丅
栤戣偼忋偺婣娨揹埑偺埵憡摿惈偩偑丄堦栚椖慠丄戝帠側婣娨揹埑偺埵憡偑僷儔偺掞峈偑彫偝偔側傞傎偳偵侽亱偐傜戝偒偔奜傟偰偄偭偰偟傑偆偺偩丅
僷儔俆侽倠兌偱偼丄侾侽俫倸偐傜俀侽倠俫傑偱偺斖埻偱埵憡嵎偼亄俆俆亱亅俀侽亱偲戝偒偔峀偑偭偰偟傑偆丅
俶倧亅侾俇俉僀僐儔僀僓乕偼揹棳弌椡偱偁傞僀僐儔僀僓乕傾儞僾偲俶俥俛慺巕傪慻傒崌傢偣偰乽棟憐俶俥宆僀僐儔僀僓乕乿傪幚尰偟偰偄傞丅
偑丄慻傒崌傢偝傟偨俶俥俛夞楬偑僴僀僀儞僺乕僟儞僗偱偁傞偨傔丄偦偺棟憐忬懺傪曐偮偨傔偵偼偦偺弌椡偼僀僐儔僀僓乕慺巕偺掅堟偱偺僀儞僺乕僟儞僗乮俉俀侽倠兌掱搙乯埲忋偺僴僀僀儞僺乕僟儞僗偱庴偗傞偙偲偑棟憐乮昁梫乯偩丅
俶倧亅侾俇俉偱偼僼儔僢僩傾儞僾弶抜偺俲俀係俇僎乕僩掞峈俈俆侽倠兌偱庴偗偰偄傞偑傕偪傠傫俉俀侽倠兌偱庴偗偨曽偑椙偄偺偩丅嬥揷愭惗傕偦傠偦傠恑偺掞峈偑恠偒偰偒偨偺偩傠偆偐丅婱廳側俉俀侽倠兌偼暿偺梡搑乮椺偊偽俼俬俙俙慺巕乯偺偨傔偵壏懚偝傟偨偺偩丄側傫偰憐憸偡傞偺偩偑偳偆偩傠偆丅
乮俀侽侽俁擭侾寧侾俋擔乯
仜姰慡懳徧摦嶌
偦偺堄枴偡傞偲偙傠偼夞楬撪偱俹俹摦嶌傪峔惉偡傞慺巕偺摦嶌偑姰慡偵懳徧偱丄擖椡偝傟偨怣崋偺僾儔僗儅僀僫僗偵旕懳徧側榗傒傪惗偠側偄丄偲偄偆偙偲偱偁傠偆丅
嬥揷幃俢俠傾儞僾偱偼揙掙偟偰偙偺旕懳徧傪側偔偡搘椡傪偟偰偄傞丅偦偺媶嬌偑姰慡懳徧摦嶌偱偁傠偆丅
弶抜嵎摦傾儞僾
弶抜嵎摦傾儞僾偼俲俁侽偺弌椡僀儞僺乕僟儞僗偑晧壸偺侾丏俉倠兌偵斾偟偰梱偐偵崅偄偐傜揹棳弌椡傾儞僾偱偁傞丅揹棳弌椡偺堄枴偼擖椡怣崋Vi乮揹埑儀僋僩儖乯偑揹棳儀僋僩儖偱弌椡偝傟傞偲偄偆偙偲偩丅偦偺弌椡揹棳抣傪I偲偡傟偽丄俬亖Vi仏倗倣乮憡屳僐儞僟僋僞儞僗丗梫偡傞偵俧俽娫侾倁偺擖椡揹埑偑壗俙偺僪儗僀儞揹棳偵曄姺偝傟傞偐乯偱偁傞丅偩偐傜揹棳乮倓俛乯僾儘乕僽傪庢傝晅偗偰弌椡揹棳傪娤應偡傞丅偙偆偡傞偲弶抜偺倗倣偑娙扨偵應掕偱偒傞丅
僆乕儉偺朄懃偐傜弶抜偺晧壸掞峈侾丏俉倠兌偵敪惗偡傞揹埑傪娤應偟偰傕傛偄丅偦偺曽偑弶抜偺揹埑僎僀儞傪懄寁嶼偱偒偰曋棙偩丅偩偐傜揹埑乮倓俛乯僾儘乕僽傕庢傝晅偗傞丅偙傟偱揹埑僎僀儞偑捈撉壜擻偵側傞丅
懳徧摦嶌偱偁傞偲偡傞埲忋丄埵憡傕懳徧偱偁傞昁梫偑偁傞丅偦偙偱弶抜晧壸掞峈侾丏俉倠兌偵敪惗偡傞揹埑偺埵憡傪揹埑乮埵憡乯僾儘乕僽偱娤應偡傞丅弶抜偼偄傢備傞埵憡斀揮夞楬偱偁傞偐傜偦傟偧傟偺埵憡偼侾俉侽亱偢傟偨傕偺偵側傞偼偢偩丅
夞楬偼俶倧亅侾俇俉僼儔僢僩傾儞僾偵弌棃傞偩偗嬤偄傕偺偲偟偨丅偑丄弶抜掕揹棳夞楬偺俿俼偲廔抜俿俼偼丄俠侾俈俈俆傗俠俋俆俋偑側偄偺偱俠侾俉侾俆偱戙梡偩丅偙偺偨傔廔抜偼俠俋俆俋偺俠倧倐偲嬤偔側傞傛偆俛亅俠娫偵俁侽倫俥傪奜晅偗偟偨丅俀抜栚嵎摦傾儞僾偼儈儔乕岠壥傪幷抐偟偨偄偺偱僇僗僐乕僪傾儞僾傪晅壛偟偨丅
傾儞僾擖椡偵侾倁俙們傪壛偊偰憗懍俼倳値偡傞丅寢壥偑壓偺僌儔僼丅墶幉偼廃攇悢丅廲幉偼倓俛偩偑丄埵憡偵娭偟偰偼亱乮搙乯偩丅
僌儔僼撪偺慄偼丄壓偺杴椺偱俬俽倓俛偲偁傞偺偑揹棳棙摼乮倓俛乯丄倁倓俛偲偁傞偺偑揹埑棙摼乮倓俛乯丄倁俹偲偁傞偺偑揹埑埵憡乮搙乯偱偁傞丅偑丄僌儔僼偑尒偵偔偄丅忋偐傜俼侾懁偺揹埑埵憡丄俆倓俛晅嬤偵俀杮廳側偭偰偄傞偺偑揹埑棙摼乮倓俛乯丄偦偺壓偺侽亱偵偁傞偺偑俼俀懁偺揹埑埵憡丄堦斣壓偺亅俇侽倓俛晅嬤偵俀杮廳側偭偰偄傞偺偑揹棳棙摼乮倓俛乯偺慄偱偁傞丅
揹棳棙摼乮倓俛乯偼亅俆俋倓俛偲偄偭偨偲偙傠偩偑丄偙傟偼侾倁擖椡偵懳偟偰侾俙丄偡側傢偪憡屳僐儞僟僋僞儞僗偑侾乮倗倣亖侾俽乯偱偁傞応崌偑侽倓俛側偺偱偁傞丅廬偭偰亅俆俋倓俛佮侾乛俋侽侽偩偐傜丄亖侾乛俋侽侽俽佮侾丏侾倣俽丄偡側傢偪偙偺夞楬偺弶抜偺倗倣偼侾丏侾倣俽偱偁傞偲偄偆偙偲偵側傞丅弶抜偼嵎摦傾儞僾偺曅曽偵偟偐擖椡偑側偄偺偱傕偲傕偲倗倣偼慺巕杮棃偺倗倣偺敿暘偵側傞丅偝傜偵僜乕僗偵擖偭偨侾侽侽兌偵傛傝揹棳婣娨偑妡偐傞偺偱偦偺暘倗倣偼彫偝偔側傞丅傑丄幚嵺偺俲俁侽傕偦傫側傕偺偩傠偆丅
栤戣偺懳徧惈偩偑弶抜偺揹棳棙摼偼侾侽俵俫倸挻傑偱傛偔懙偭偰偄傞丅偙傟偼俲俁侽偺杮棃偺擻椡偑帵偝傟偰偄傞傕偺偱偁傝丄傑偨嵎摦傾儞僾偑桪傟偨懳徧惈傪敪婗偡傞偙偲傪帵偡傕偺偱傕偁傞丅
揹埑棙摼乮倓俛乯偼俇倓俛掱搙偩傠偆偐丅倗倣亖侾丏侾偱偁傞偲弶抜偺揹埑僎僀儞偼侾丏俉倠兌亊侾丏侾倣俽亖侾丏俋俉攞佮俇倓俛偱偁傞偐傜懨摉側寢壥偱偁傞丅
揹埑僎僀儞乮倓俛乯偼丄嵍塃偲傕侾俵俫倸晅嬤傑偱僼儔僢僩偩丅偑丄俆俵俫倸挻偺椞堟偱偼懳徧偱偼側偔側偭偰偄傞丅
埵憡偼俁俵俫倸傑偱偼侾俉侽亱偢傟偰椙偔懳徧惈傪曐偭偰偄傞丅偑丄偦傟埲忋偺椞堟偱偼懳徧惈偼曵傟偰偄傞丅
偙偺寢壥偐傜偡傞偲丄弶抜偼憤偠偰俁俵俫倸掱搙傑偱偼椙偔懳徧摦嶌偟偰偄傞偲尵偊傞偩傠偆丅偑丄偦傟埲忋偺椞堟偱偼慺巕乮弶抜偐俀抜栚乯偺崅堟尷奅揑梫慺偱懳徧惈偑幐傢傟偰偄偔丅
偙偺寢壥偐傜偡傞偲丄偙偺傾儞僾偵俶俥俛傪妡偗傞応崌偼俁俵俫倸埲忋偺椞堟偼儖乕僾僎僀儞侾埲壓偵捑傔偨偄姶偠偱偼偁傞丅
俀抜栚嵎摦傾儞僾
俀抜栚嵎摦傾儞僾傕揹棳弌椡偱偁傞丅偲尵偆傛傝丄偙偺俀抜栚嵎摦傾儞僾偑揹棳弌椡偱偁傞偙偲偑姰慡懳徧傾儞僾偺嵟傕廳梫側億僀儞僩側偺偱偁傞丅栜榑棟憐揑側揹棳弌椡亖弌椡僀儞僺乕僟儞僗亣丂偼崲擄偩偑丄偦偙偼尰幚偵偼庴偗傞懁乮偙偙偱偼廔抜乯偺擖椡僀儞僺乕僟儞僗偲偺憡懳揑娭學偵側偭偰丄庴偗傞懁偺擖椡僀儞僺乕僟儞僗傛傝俀抜栚偺弌椡僀儞僺乕僟儞僗偑憡懳揑偵崅偗傟偽崅偄傎偳棟憐揑側姰慡懳徧傾儞僾偵側傞偺偱偁傞丅
偩偐傜揹棳僾儘乕僽傪庢傝晅偗偰弌椡揹棳傪娤應偡傞丅偙偆偡傞偲俀抜栚偺倗倣傕應掕偱偒傞偩傠偆丅
偱偼丄偦偺揹棳弌椡偱俀抜栚嵎摦傾儞僾偺晧壸乮偲巚傢傟傞乯侾丏俇倠兌偵惗偠傞揹埑偲偦偺埵憡偼偳偆側傞偺偱偁傠偆丅揹埑乮倓俛乯僾儘乕僽偲揹埑乮埵憡乯僾儘乕僽傕庢傝晅偗偰娤偰傒傛偆丅
寢壥偼壓偺僌儔僼丅尒曽偼弶抜偺応崌偲摨偠偩丅
忋偐傜俼俋懁偺揹埑埵憡丄俼俉懁偵偍偗傞揹埑棙摼乮倓俛乯丄俼俋懁偵偍偗傞揹埑棙摼乮倓俛乯丄俼俉懁偺揹埑埵憡丄堦斣壓偵俀杮廳側偭偰偄傞偺偑揹棳棙摼乮倓俛乯偺慄偱偁傞丅
揹棳棙摼乮倓俛乯偼亅俆侽倓俛偲偄偭偨偲偙傠偩偑丄偙傟偼弶抜傊偺侾倁擖椡偵懳偟偰侾俙丄偡側傢偪憡屳僐儞僟僋僞儞僗偑侾俽偱偁傞応崌偑侽倓俛丅廬偭偰亅俆侽倓俛佮侾乛俁侽侽偩偐傜丄亖侾乛俁侽侽俽佮俁丏俁俁倣俽偲側傞偺偩偑丄偙傟偼弶抜偺倗倣偵俀抜栚偺倗倣偑崌嶼偝傟偨悢抣偱偁傞偐傜丄俀抜栚扨撈偺揹棳棙摼偼俁丏俁俁乛乮侾丏侾仏侾丏俉乯亖侾丏俇俈倣俽偱偁傞丅偲偄偆偙偲偵側傞丅
偙偆偟偰傒傟偽丄忋偺弶抜偩偗偺倗倣傕侾侽俵俫倸挻偺懷堟傑偱椙偔懙偭偰偄偨偑丄弶抜亄俀抜栚偱傕侾侽俵俫倸傑偱偼幚偵椙偔懙偭偰偄傞丅揹棳弌椡傾儞僾偺揹棳僎僀儞偑偙偙傑偱懙偭偰偄傟偽丄偙傟偩偗偱旕忢偵桪傟偨懳徧摦嶌偟偰偄傞丄偲偄偆偙偲偵側傞偺偩偑丄杮棃偼乮丱丱丟
埵憡偵偮偄偰偼弶抜偲侾俉侽亱斀揮偟偰偄傞丅傑偨埵憡偑夞揮傪巒傔傞廃攇悢偑弶抜偲斾妑偟偰侾寘壓偑偭偰偄傞丅偙傟偼廔抜俿俼偺俠倧倐乮偙偙偱偼俠俋俆俋憡摉偲偡傞偨傔俛亅俠娫偵俁侽倫俥傕奜晅偗偟偰偄傞乯偲俼俉丆俼俋偵傛偭偰帪掕悢偑惗偠偨偙偲偵傛傞傕偺偩偑丄偙傟傕侾俵俫倸掱搙傑偱椙偔懳徧惈偑曐偨傟偰偄傞丅侾俵俫倸挻偺懷堟偱偺旕懳徧惈偼偳偆傕弶抜乮偲俀抜栚偺擖傝岥乯偐傜堷偒偢偭偰偄傞姶偠偩丅
偝偰丄俼俉丆俼俋偵偍偗傞揹埑棙摼乮倓俛乯偵偮偄偰偼慡偔懙偭偰偄側偄丅廬偭偰懳徧偱偼側偄丅
偲尵偭偨恖傕偄偨偺偱丄偙傟偩偗壓偱奼戝偟偰傒傛偆丅
偙傟偑俼俉丆俼俋忋抂偱偺揹埑棙摼乮倓俛乯偱偁傞丅偙傟偵傾儞僾弌椡揰偱偺揹埑棙摼乮倓俛乯偺僌儔僼傪壛偊丄弌椡抜乮廔抜乯忋懁偑僄儈僢僞僼僅儘傾偩偐傜摉慠偺寢壥偩丄偲偍偭偟傖偭偨曽傕偁偭偨丅偺偱丄偙偙偱傕傾儞僾弌椡揰偱偺揹埑棙摼乮倓俛乯偺僌儔僼傪壛偊偰傒偨丅偦傟偑壓偺杴椺偱亊倁倓俛乮俼侾侾丗俀乯偲側偭偰偄傞慄偱丄杦偳俼俉忋抂偺揹埑棙摼乮倓俛乯偺慄偲廳側偭偰偄傞丅偑丄挻崅堟傪尒傞偲暘偐傞傛偆偵丄偛偔嬐偐偵僎僀儞偼彮側偄丅
傑偝偵偳偙偐偱尒偨偺偲慡偔摨偠僔儈儏儗乕僔儑儞寢壥偱偁傞丅
傗偼傝俀抜栚嵎摦傾儞僾偼忋懁偺僎僀儞偑壓懁傛傝偢偭偲戝偒偔偰旕懳徧側偺偩丅
偙偺俀抜栚偺旕懳徧傪丄廔抜忋懁偑僎僀儞侾枹枮偺僄儈僢僞僼僅儘傾丄廔抜壓懁偑僄儈僢僞愙抧偱僎僀儞壱偄偱偄傞偲偄偆偙偲偵傛偭偰捯咫傪崌傢偣偰偄傞偺偩丅
偙傟偱偼懳徧偱偼側偄丅
偲偄偆晽偵杮摉偵偍峫偊偩偭偨偺偐偳偆偐偼暘偐傜側偄偑丄俀抜栚偺僎僀儞偺晄懙偄傪偦偆忋庤偔廔抜偺摦嶌宆幃偺堘偄偱崌傢偣傜傟傞偼偢傕側偄偱偟傚偆偵丒丒丒僄儈僢僞僼僅儘傾偼晧壸偱揹埑僎僀儞偼杦偳曄傢傜側偄偗偳丄僄儈僢僞愙抧偼晧壸偱戝暆偵揹埑僎僀儞偑曄傢傞傫偱偡傛偹丒丒丒乮亅亅乯
愭偵恑傓慜偵偙偺僌儔僼偱廔抜帺懱偺揹埑棙摼偑暘偐傞丅偺偱丄屻偺偨傔偵寁嶼偟偰偍偔丅係俆倓俛亅侾俁倓俛亖俁俀倓俛乮亖係侽攞乯偩丅
偝偰丄
幚偺偲偙傠丄妋偐偵俀抜栚嵎摦傾儞僾偺忋懁偺曽偑偦偺晧壸偑戝偒偄偺偱丄寢壥懳傾乕僗偱尒偨応崌偺揹埑棙摼乮倓俛乯偼忋懁偺曽偑戝偒偔側傞偺偱偁傞丅乮揹埑棙摼僾儘乕僽偺昞帵偼懳傾乕僗偱偺棙摼昞帵偱偁傞丅乯
偙偺揰偱偼俀抜栚忋壓偼妋偐偵旕懳徧惈傪桳偟偰偄傞丅
傑偨丄偙偺奜柺揑尰徾傪傕偭偰廔抜忋懁偼僄儈僢僞僼僅儘傾偱偁傞丄偲尵偆偺傕丄掕媊偐傜偡傟偽娫堘偄偱偼側偄丅
偑丄偦偙偱巭傑偭偰偟傑偆偲丄姰慡懳徧宆傾儞僾偵偮偄偰偼偦傟埲忋偺摦嶌棟夝偑崲擄偵側偭偰偟傑偆偺偩丅
偦傟偼丄擣幆偺夁掱偱曋媂偺偨傔偵嶌傜傟偨椶宆壔乮掕媊乯偼摉慠姰慡側傕偺偱偼側偄偺偱丄偦偺尷奅傪傢偒傑偊偰師偺師尦偵恑傓傋偒側偺偵丄椶宆壔乮掕媊乯偵峉揇偟偰偲傜傢傟偰偟傑偆偲偝傜偵恑傫偩擣幆偑弌棃側偔側偭偰偟傑偆偲偄偆丄偙偺悽偱偼偳偙偵傕傛偔尒傜傟傞尰徾偩丅
傑偁丄傢偞偲鎘曎偲偟偰巊偆偙偲傕偁傞偑乮丱丱丟
椺偺俁愙抧摦嶌嬫暘偼丄娙曋偵摦嶌奣擮傪棟夝偝偣傞偨傔偺丄揹埑僪儔僀僽傪埫栙偺椆夝偲偟偨丄弶怱幰梡偺曋媂揑椶宆壔偱偁傞丅偩偐傜丄偁偺僄儈僢僞僼僅儘傾乮僐儗僋僞愙抧乯摦嶌傕揹棳僪儔僀僽偟偰偟傑偆偲丄偙偺椶宆壔偱嶌傜傟偨偄傢備傞揟宆揑僄儈僢僞僼僅儘傾摦嶌奣擮偲偼戝暘堘偭偨條憡傪帵偡傕偺偵側傞偺偱偁傞丅
偙偙偺偲偙傠傪扨弮偵擖弌椡揹埑傗怣崋偺壛偊曽庢傝弌偟曽偩偗偱僄儈僢僞僼僅儘傾摦嶌偱偁傞偲愢柧偡傞偲丄掕媊偐傜偦偆偩丄偲偄偆偩偗偱丄偱偼偙偙偱壗屘廔抜忋懁偺擖椡揹埑乮亖俀抜栚忋懁偺弌椡揹埑乯偑壓懁傛傝戝偒偔側傞偺偐丠偲偐丄偦傟偼廔抜忋懁偺擖椡僀儞僺乕僟儞僗偑崅偄偐傜偩偲偟偰傕丄偱偼壗屘偦偺擖椡僀儞僺乕僟儞僗偑崅偔側傞偺偐丠丂側偳偺摦嶌偺場壥棩偑愢柧乮擣幆乯偱偒側偔側偭偰偟傑偆偺偱偁傞丅
偱丄弴斣偵捛偆丅
(1)丂愭偢丄俀抜栚嵎摦傾儞僾偑揹棳弌椡偱偁傞偙偲偑梫乮僇僫儊乯偩丅
(2)丂偙偺偨傔廔抜忋壓偺僩儔儞僕僗僞偺儀乕僗掞峈侾丏俇倠兌偵偼摍偟偄懳徧側揹埑偑敪惗偡傞偺偱偁傞丅
幚嵺忋壓偺侾丏俇倠兌偵敪惗偡傞揹埑傪揹埑嵎乮倁乯僾儘乕僽偱娤偰傒傛偆丅
俁侽侽倠俫倸挻偺懷堟偱忋壓偺揹埑偑旝柇偵堎側傝偼偠傔丄懳徧惈偑曵傟巒傔傞偑丄偙偺侾丏俇倠兌偺椉抂偵惗偠傞揹埑偑偙偺椞堟傑偱堦抳偟偰偄傞偙偲丄偙偙偑杮棃俀抜栚嵎摦傾儞僾偺揹埑棙摼偺懳徧惈傪榑偠傞傋偒応強側偺偩丅壗屘側傜偙傟偑屘偵廔抜忋壓偼偄傢備傞僄儈僢僞愙抧摦嶌傪偟偰丄摍偟偄揹棳仌揹埑棙摼傪敪惗偡傞偙偲偵側傞偐傜偱偁傞丅
偝偰丄愭偵傒偨傛偆偵俀抜栚傑偱偺倗倣偼俁丏俁俁倣俽偱偁偭偨丅偱偁傟偽侾丏俇倠晧壸偵惗偠傞揹埑偼侾丏俇倠亊俁丏俁俁倣俽亖俆丏俁俀俉倁偲側傞偼偢偱偼側偐傠偆偐丅側偺偵僌儔僼偱偼掅堟偱係丏俆倁偩丅
偦傟偼丄廔抜偑僩儔儞僕僗僞偱偁傞偨傔偵偦偺擖椡僀儞僺乕僟儞僗偑侾丏俇倠兌偵僷儔偱棙偄偰偄傞偨傔偩丅廔抜偑恀嬻娗傗俥俤俿偱偁傟偽擖椡僀儞僺乕僟儞僗偑柍帇偱偒傞傎偳崅偄偺偱寁嶼捠傝偵俆丏俁俀俉倁偵側傞偩傠偆丅媡偵尵偊偽偙傟偱廔抜俿俼偺擖椡僀儞僺乕僟儞僗傪寁嶼偱媮傔傞偙偲偑偱偒傞偙偲偵側傞丅俁丏俁俁亊倃亖係丏俆偲側傞倃亖侾丏俁俆倠兌偱偁傞偐傜丄侾丏俇倠兌偲僷儔偵偟偰侾丏俁俆倠兌偲側傞偺偼俉丏俈倠兌偱偁傞丅廬偭偰丄廔抜俿俼偺擖椡僀儞僺乕僟儞僗偼掅堟偱俉丏俈倠兌偱偁傞偲偄偆偙偲偵側傞偺偱偁傞丅栜榑偦偺悢抣偼僄儈僢僞偵擖偭偰偄傞係俈兌偺掞峈偵傛傞揹棳婣娨岠壥傕壛傢偭偰偺傕偺偩丅
偙偙偱丄偙傟偲忋偱尒偨揹棳棙摼乮倓俛乯偺僌儔僼乮侾俵俫倸挻傑偱僼儔僢僩偵怢傃偰偄偨乯偲揹埑乮埵憡乯偺僌儔僼乮栺俋侽倠俫倸偱係俆亱偺埵憡抶傟丄懄偪戞堦億乕儖倖倧佮俋侽倠俫倸乯偲傪崌傢偣偰峫偊傛偆丅
侾丏俇倠兌偺椉抂揹埑傕俋侽倠俫倸晅嬤偱掅堟偺亅俁倓俛乮係丏俆乛侾丏係侾係俀侾俁俆俇亖俁丏侾俉俀倁乯偵側偭偰偄傞偱偼側偄偐丅揹棳僎僀儞偼侾俵俫倸挻傑偱怢傃偰偄傞偺偵丄偩丅
懄偪侾丏俇倠兌椉抂偺揹埑抣偺僌儔僼偼丄偙偙偵惗偠偰偄傞帪掕悢偺寢壥側偺偱偁傞丅
偦偆偡傞偲丄侾丏俇倠兌偲廔抜俿俼偺擖椡僀儞僺乕僟儞僗俉丏俈倠兌偺僷儔儗儖掞峈抣侾丏俁俆倠兌偑僪儔僀僽僀儞僺乕僟儞僗俼丄廔抜俿俼偺俠倧倐偑俠偲側偭偨帪掕悢偩偲偄偆偙偲偵堘偄側偄偺偩偑丄偦傟偑忋壓偱偙傟傎偳堦抳偟偰偄傞偲偄偆偙偲傪偙偺僌儔僼偼帵偟偰偄傞偺偱偁傞丅廔抜壓懁偼揟宆揑僄儈僢僞愙抧摦嶌偵堘偄側偄偐傜丄廔抜壓懁俿俼偺俠倧倐偼儈儔乕岠壥偱侾亄廔抜偺揹埑僎僀儞攞乮亖係侽攞乯偵側傞偼偢偩丅偙傟偵懳偟偰廔抜忋懁偑僄儈僢僞僼僅儘傾偱偁傞偲偡傞偲忋懁俿俼偺俠倧倐偵偼儈儔乕岠壥偑摥偐側偄偼偢偩丅
偩偐傜丄廔抜偺忋懁偑僄儈僢僞僼僅儘傾摦嶌偱壓懁偼僄儈僢僞愙抧摦嶌偱偁傞偲偟偨応崌丄僎僀儞偩偗偱側偔億乕儖傑偱偙傫側偵堦抳偡傞偙偲傪偄偐偵偟偰愢柧偡傞偺偩傠偆偐丅
偙傟偼傗偼傝廔抜忋壓偼奜尒揑偵堘偭偨摦嶌傪偡傞傛偆偵尒偊傞偑偳偪傜傕僄儈僢僞愙抧摦嶌傪偟偰偄傞丄偲尵偭偨曽偑傛偝偦偆偩丅偲偄偆偙偲偑傕偆偙傟偩偗偱傕暘偐傞偺偱偁傞丅乮丱丱丟
(3)丂僩儔儞僕僗僞偺擖椡僀儞僺乕僟儞僗偼忋壓偲傕乮Hie亄Hfe仏係俈兌乯摍偟偄偺偱丄寢壥忋壓偺僩儔儞僕僗僞乕偵偼摍偟偄儀乕僗揹棳偑棳傟丄偙傟偑Hfe攞偲側偭偰丄忋壓偺僩儔儞僕僗僞乕偼摍偟偄僐儗僋僞揹棳丄僄儈僢僞揹棳傪弌椡偡傞丅
(4)丂偙偺嵺丄俀抜栚嵎摦傾儞僾偑揹棳弌椡偱偁傞偨傔偵丄偙偺廔抜僐儗僋僞揹棳傕僄儈僢僞揹棳傕摍偟偔慺巕屌桳偺摿惈偲偟偰弌椡僀儞僺乕僟儞僗偑崅偄丄梫偡傞偵揹棳弌椡偲側傞偺偱偁傞丅俀抜栚偺弌椡僀儞僺乕僟儞僗偑崅偄偙偲偑梫乮僇僫儊乯側偺偩丅
壗屘側傜丄
嘆俀抜栚嵎摦傾儞僾偑揹棳弌椡側偺偱丄偦偺揹棳偺宱楬偲偟偰侾丏俇倠兌偺愭偵傾儞僾偺晧壸乮俶倧亅侾俇俉偱偼侾倠兌乣俆侾倠兌乯偑宷偑傝丄偙偺偨傔俀抜栚忋懁俿俼偐傜尒偨廔抜偺擖椡僀儞僺乕僟儞僗偑丄廔抜偺揹棳僽乕僗僞乕岠壥乮廔抜偺揹棳僎僀儞乯偵傛傝丂
亖侾丏俁俆俲兌乮廔抜俿俼偺擖椡僀儞僺乕僟儞僗乯亄晧壸乮侾倠兌乣俆侾倠兌乯亊廔抜揹棳僎僀儞乮奣嶼侾丏俇倠乛係俈亖俁係乯亊俀乮廔抜俙媺俹俹側偺偱乯
亖俈侽丏俈倠兌乣俁丏係俈俵兌
偲崅偔側偭偰傕丄俀抜栚偼壗傜偍偐傑偄側偟偵怣崋捠傝偺揹棳傪弌椡偡傞偺偱丄廔抜忋壓偺僩儔儞僕僗僞偺儀乕僗掞峈侾丏俇倠兌偵偼曄傢傜偢怣崋捠傝偺摍偟偄懳徧側揹埑偑敪惗偡傞偐傜丅偱偁傝丄
嘇傑偨丄摨偠偔俀抜栚嵎摦傾儞僾偑揹棳弌椡偱偁傞偨傔偵丄揹埑僪儔僀僽偱偁傟偽廔抜俿俼偺僄儈僢僞揹棳偑晧壸偵棳傟偰惗偠傞弌椡揹埑偑擖椡懁偺擖椡揹埑傪堷偒壓偘傞偲偄偆俶俥俛岠壥丄偄傢備傞揹棳婣娨嶌梡偑夞旔偝傟偰偄傞偐傜丅
偱偁傞丅
捠忢偺僄儈僢僞僼僅儘傾偼揹埑僪儔僀僽側偺偱丄僄儈僢僞掞峈偑擖偭偰偄傞偲偙傟偵惗偠偨揹埑偑擖椡揹埑傪尭偠傞曽岦偵摥偔丅偙傟偑揹棳婣娨偲偄偆俶俥俛偩丅偙偺偨傔僄儈僢僞懁偺弌椡僀儞僺乕僟儞僗偼壓偑偭偰揹埑弌椡偵側傞偺偩丅偑丄偙偺傛偆偵揹棳婣娨偱俶俥俛偑摥偔偺偼丄怣崋尮偑揹埑僪儔僀僽偱偁傞偨傔偵丄儀乕僗揹埵偑擖椡懁偺揹埵偵婯掕偝傟偰偟傑偆偨傔偵偦偆側傞偺偱偁傞丅
姰慡懳徧宆偺傛偆偵揹棳僪儔僀僽偡傞偲丄摨偠偔僄儈僢僞掞峈偵揹埑偑惗偠偰傕丄擖椡揹埑偺曽傕偙傟偵崌傢偣偰帺桼偵摝偘傞傛偆偵忋偑偭偰偄偔偺偩丅偩偐傜揹棳婣娨偲偄偆俶俥俛偑摥偐側偄丅偙偺俶俥俛偑摥偐側偄偺偱丄僄儈僢僞懁傕僐儗僋僞懁偲摨偠偔弌椡僀儞僺乕僟儞僗偺崅偄揹棳弌椡偱偁傞偲偄偆慺巕杮棃偺惈幙偵側傞偺偱偁傞丅傑偨丄偙偺俶俥俛偑摥偐側偄偺偱僄儈僢僞懁偐傜弌椡傪庢傝弌偟偰傕僐儗僋僞懁偐傜庢傝弌偟偨応崌偲摨條偺揹棳丒揹埑僎僀儞傪帩偮偺偱偁傞丅
梫偡傞偵丄揹埑僪儔僀僽偼帺暘偱揹埑傪寛傔傞丅揹棳偼晧壸偵傛偭偰寛傑傞丅揹棳僪儔僀僽偼帺暘偱揹棳傪寛傔傞丅揹埑偼晧壸偵傛偭偰寛傑傞丅偲偄偆摉偨傝慜偺偙偲側偺偩丅
偙偺擇偮偺寢壥偼奜尒忋偼摨偠偱偁傞丅偑丄場壥娭學偑媡側偺偩丅
揹埑嵎僾儘乕僽傪偝傜偵忋懁侾丏俇倠兌偲傾乕僗娫丄傾儞僾弌椡抂巕乮俼侾侾忋抂乯偲傾乕僗娫偵傕宷偄偱偁傢偣偰娤偰傒傛偆丅
忋偵俀杮廳側偭偰偄傞偺偑俼俉忋抂亅傾乕僗娫揹埑偲俼侾侾忋抂亅傾乕僗娫揹埑乮亖傾儞僾弌椡揹埑乯偱偁傝丄壓偼幚偼俁杮偑廳側偭偰偄偰丄侾俵俫倸晅嬤偱忋偵側傞偺偑俼俋偺椉抂揹埑丄偦偟偰侾俵俫倸晅嬤偱壓偵側傞偺偑俼俉偺椉抂揹埑偲丄俼俉忋抂亅傾乕僗娫揹埑偐傜俼侾侾忋抂亅傾乕僗娫揹埑乮亖傾儞僾弌椡揹埑乯傪堷偄偨揹埑偺慄偱偁傞丅侾杮偵偟偐尒偊側偄偑偦傟偼偙傟傜偑姰慡偵廳側偭偰偄傞偨傔偱偁傞丅
偙傟傪傕偭偰弌椡抜偺忋抜偺僎僀儞偑尭悐偟偰偄傞丅僄儈僢僞僼僅儘傾偱偁傞偐傜摉慠偱偁傞丅偲尵偭偰偟傑偆偲丄僄儈僢僞僼僅儘傾偺尭悐棪偼廔抜慺巕偺屌桳偺倗倣乮憹暆擻椡乯偵婯掕偝傟傞偺偱丄壗屘俼俉忋抂亅傾乕僗娫揹埑偲俼侾侾忋抂亅傾乕僗娫揹埑乮亖傾儞僾弌椡揹埑乯偺嵎揹埑偑俼俋椉抂揹埑偲傕堦抳偡傞偙偲偵側傞偺偐傪慡偔愢柧偱偒側偄丅
堘偆偺偩丅摨偠偔捈姶揑側尵偄曽傪偡傞偺偱偁傟偽丄俼俉忋抂偺揹埑偑傾儞僾弌椡揹埑偵廬偭偰丄傾儞僾弌椡揹埑亄俼俉椉抂揹埑偱摦偄偰偄傞乮怳傜傟偰偄傞乯偺偱偁傞丅僄儈僢僞揹埵偑儀乕僗揹埵偵廬偆偑屘偵僄儈僢僞僼僅儘傾偲偄偆偺偱偁傟偽丄偙偙偼儀乕僗揹埵偑僄儈僢僞揹埵偵廬偭偰偄傞偺偱丄摨條偺柦柤朄偱尵偊偽儀乕僗僼僅儘傾偲偱傕尵偆傋偒摦嶌傪偟偰偄傞偺偱偁傞丅
揹埑僪儔僀僽偼帺暘偱揹埑傪寛傔傞丅揹棳偼晧壸偵傛傞丅揹棳僪儔僀僽偼帺暘偱揹棳傪寛傔傞丅揹埑偼晧壸偵傛傞丅偺偩偑丄寢壥偼奜尒忋摨偠傛偆偵尒偊傞丅偁傢偣偰怣崋偺擖椡丄弌椡偺応強丄俁抂巕偺愙抧偺巇曽丄偺掕媊偐傜偡傞偲僄儈僢僞僼僅儘傾偩丅廬偭偰偙傟傪僄儈僢僞僼僅儘傾偩丄偲尵偭偰傕偦傕偦傕偺掕媊偑濨枂側屘偵暿偵娫堘偄偱偼側偄丒丒丒丅
偑丄彮側偔偲傕丄揹棳僪儔僀僽偵傛偭偰揹棳婣娨偑妡偐傜側偄僄儈僢僞僼僅儘傾偱偁傞丄偲丄偙偲傢傝傪擖傟傞偖傜偄偺攝椂偑昁梫偱偁傠偆丅
廔抜俽俤俹俹
傛偭偰丄廔抜偼忋壓偲傕揹棳弌椡偱偁傞丅
偲偄偆偙偲偵側傞偺偩偑丄偙傟傪妋偐傔傛偆丅
廔抜忋懁俿俼偲廔抜壓懁俿俼丄偝傜偵傾儞僾弌椡偵揹棳棙摼乮倓俛乯僾儘乕僽傪庢傝晅偗傞丅傑偨傾儞僾弌椡偵偼揹埑棙摼乮倓俛乯僾儘乕僽傕庢傝晅偗偰傾儞僾慡懱偺揹埑僎僀儞傕娤偰傒傞丅
忋偐傜弌椡揹埑棙摼乮倓俛乯丄弌椡揹棳棙摼乮倓俛乯丄堦斣壓偱俀杮廳側偭偰偄偰侾俵俫倸晅嬤偱忋偵偔傞偺偑壓懁偺俠侾俉侾俆偺曽偺揹棳棙摼乮倓俛乯偱偁傝丄侾俵俫倸晅嬤偱壓懁偵棃傞偺偑忋懁偺俠侾俉侾俆偺曽偺揹棳棙摼乮倓俛乯偱偁傞丅
揹棳棙摼乮倓俛乯偺堄枴偼愭偵弎傋偨偲偍傝偩丄
忋壓偺俠侾俉侾俆偺弌椡揰偱傕幚偵椙偔堦抳偟偰偄傞丅懳徧摦嶌傪偟偰偄傞偺偩丅
掅堟偱亅俀侾倓俛乮亖侾乛侾侾丏俁乯偱偁傞偐傜弶抜偐傜偙偙傑偱偺憡屳僐儞僟僋僞儞僗倗倣偼侾乛侾侾丏俁亖俉俉丏俆倣俽偲偄偆偙偲偵側傞丅偙傟偼弶抜亄俀抜栚偺倗倣亖俁丏俁俁偑壛傢偭偰偺傕偺偱偁傞偐傜丄廔抜帺懱偺揹棳棙摼偼俉俉丏俆乛俁丏俁俁亖俀俇丏俆俉攞偲偄偆偙偲偵側傞丅
幚偵俶倧亅侾俇俉俥俙偺憹暆擻椡偼偦偺杦偳偑廔抜偺俿俼偵傛傝扴傢傟偰偄傞丄偲偄偆偙偲偵側傞丅廔抜俿俼偱壒偑曄傢傞偲尵傢傟傞偺傕傓傋側傞偐側丄偩丅
偝偰丄偦傟偑傾儞僾弌椡偱偼揹棳僎僀儞乮倓俛乯偑俇倓俛憹偊偰亅侾俆倓俛偲側偭偰偄傞丅偙傟偼廔抜偑俙媺僾僢僔儏僾儖摦嶌偱偁傞偨傔偵僎僀儞偑攞乮亄俇倓俛乯偵側傞偐傜偱偁傞丅
偙偺亅侾俆倓俛偑偙偺俶倧亅侾俇俉僼儔僢僩傾儞僾慡懱偺憡屳僐儞僟僋僞儞僗俧俵傪昞偟偰偄傞丅亅侾俆倓俛亖侾乛俆丏俇俆亖侾俈俈倣俽偩丅
偩偐傜弌椡偵晧壸傪宷偄偩応崌偺揹埑棙摼偼俧俵乮倣俽乯亊晧壸乮倠兌乯偲側傞丅侾倠兌傪晧壸偲偡傟偽侾俈俈倣俽亊侾倠兌亖侾俈俈攞亖係係丏俋俆俋倓俛偲側傞偼偢偩丅壥偨偟偰丒丒丒壓偺僌儔僼傪尒傟偽丄弌椡揹埑棙摼偼係俆倓俛偲側偭偰偄傞丅
偦偺揹埑棙摼偼俋侽倠俫倸晅嬤偱亅俁倓俛尭悐偟丄偦傟埲忋偱偼侾俵俫倸晅嬤傑偱偼亅俇倓俛乛倧們倲偱尭悐偟偰偄傞丅偙傟偼偙傟傑偱偺夝愅偐傜廔抜俿俼偺俠倧倐偵傛傞宍惉偝傟傞帪掕悢偵傛傞傕偺偱偁傞偙偲偑柧傜偐偩偑丄偙傟偑廔抜忋壓偺俿俼偺揹棳棙摼偱傕摨偠偲側偭偰偄傞丅偙傟偼廔抜忋壓偺俿俼偑埵憡揑偵傕懳徧側摦嶌傪偟偰偄傞偲偄偆偙偲傪昞偡傕偺偩丅
侾俵俫倸晅嬤偱忋壓俿俼偺揹棳棙摼乮倓俛乯偵偼晄婯懃側曄壔偑惗偠傞偲嫟偵弌椡揹埑棙摼乮倓俛乯傕亅俇倓俛乛倧們倲埲忋偺孹偒偱尭悐懍搙傪懍傔偰偄傞丅偙偺棟桼偼晄柧偩丅偙傟偼偳偆傕弶抜嵎摦傾儞僾傪娤偨偲偒偐傜堷偒偢偭偰偄傞尰徾偺傛偆偩丅慺巕偺崅堟摿惈偺尷奅偐傕抦傟側偄偟丄姰慡懳徧摦嶌帺懱偺尷奅偐傕抦傟側偄丅俶俥俛傪妡偗傞嵺偼憗傔偵儖乕僾僎僀儞侾埲壓偵捑傔偨曽偑媑偩傠偆丅
廔抜傪壓偺傛偆偵忋壓愗傝棧偟偰丄弶抜亄俀抜栚亄廔抜偺俹俹摦嶌偺曅懁傪偦傟偧傟娤傞偙偲傕偱偒傞丅
弶抜偲俀抜栚偼嵎摦傾儞僾偱偁傝俹俹摦嶌偺曅懁偢偮偑懳徧摦嶌傪偡傞偺偼摉偨傝慜丅廔抜偼偦偆偼偄偔傑偄丅忋偺応崌偼廔抜忋壓偑俙媺俹俹摦嶌偟偰偄偨偺偱懳徧摦嶌偟偰偄偨偺偩丅偲丄巚偆恖傕偄傞偐傕抦傟側偄丅曅懁偢偮娤傟偽柧傜偐偵側傞丅
弌椡偺揹埑棙摼乮倓俛乯偲偦偺揹埑偺埵憡傪忋壓偦傟偧傟偵娤傞丅
廔抜忋壓傪愗傝棧偡偲俢俠僶儔儞僗偑摉慠曵傟傞丅偙偺偨傔忋壓偺俙俠摦嶌傕傗傗曵傟傞偺偩偑丄偦傟偱傕廫暘側寢壥偩傠偆丅偦傟偧傟偺揹埑棙摼乮栺俁俋倓俛乯丄弌椡揹埑偺埵憡乮僎僀儞偑曅懁偺偨傔偵敿暘偲側偭偨偺偱亅俁倓俛揰偑侾俇侽倠俫倸偵怢傃偰偄傞乯偲傕挻崅堟傪彍偗偽幚偵椙偔懙偭偰偄傞丅
偙傟偼幚偵旕杴側懳徧摦嶌偱偁傞丅偲尵偆埲奜偵側偄丄偲巹偵偼巚偊傞偑乮丱丱丟
嶲峫傑偱偵変偑俶倧亅侾俇俉俥俙偺俀抜栚俿俼僶乕僕儑儞儌僨儖偱摨條偺偙偲傪偟偰傒傞丅
俥俤俿僶乕僕儑儞偵斾傋俇倓俛掱搙僎僀儞偑戝偒偄偑丄偙傟傕幚偵忋庤偔偄偭偰偄傞丅乮丱丱乯
偝偰丄廔抜忋壓偺俿俼偺俠倧倐乮俥俤俿偱偁傟偽俠倰倱倱乯偵傛偭偰惗偠傞帪掕悢偼壗屘偙傫側偵堦抳偡傞偺偩傠偆偐丅
幚偼廔抜忋壓偺俿俼偺俠倧倐乮俥俤俿偱偁傟偽俠倰倱倱乯偡側傢偪弌椡梕検偵傛偭偰惗偠傞帪掕悢偼偙偺僔儈儏儗乕僔儑儞傪偡傞傑偱偼忋壓偱堎側傞傕偺偲巚偭偰偄偨丅偙傟偑俲幃姰慡懳徧宆傾儞僾偺桞堦偺旕懳徧惈偩偲巚偭偰偄偨偺偱偁傞丅
偑丄僔儈儏儗乕僔儑儞寢壥偼偙傟偑姰慡偲尵偭偰偄偄傎偳偵堦抳偡傞偙偲傪帵偟偰偄傞丅
廔抜壓懁偼揟宆揑側僄儈僢僞愙抧摦嶌偩偐傜丄嫵壢彂偳偍傝丄儈儔乕岠壥偵傛傝俠倧倐偼廔抜偺揹埑僎僀儞傪俙偲偟偰俠倧倐仏乮侾亄俙乯偵奼戝偝傟丄寢壥倖們亖侾乛乮俀兾俼俠仏乮侾亄俙乯乯偺帪掕悢乮億乕儖乯偑敪惗偡傞丅
寁嶼偟偰傒傛偆丅偙傟傑偱偺夝愅偱丂俼亖侾丏俁俆倠兌丂俙亖係侽丂偑柧傜偐偵側偭偰偄傞丅俠侾俉侾俆偺俠倧倐偼婯奿偱偼俀倫俥偩丅俠俋俆俋憡摉偵偡傞偨傔俛亅俠娫偵俁侽倫俥傪奜晅偗偟偰偄傞偐傜丄俠亖俁俀倫俥偲偡傞丅
倖們亖俉俋丏俉倠俫倸丂傄偭偨傝偩丅
偙傟偵懳偟偰丄廔抜忋懁偼揹棳揑偵尒偨幚憸偼偄傢備傞僄儈僢僞愙抧摦嶌偩偑丄奺晹傪揹埑揑偵尒偨嫊憸偼僄儈僢僞僼僅儘傾摦嶌側偺偱丄偟偨偑偭偰揹埑偱棙偔俠倧倐偺儈儔乕岠壥偼敪惗偟側偄偼偢丅傛偭偰忋懁偺帪掕悢偼侾乛乮俀兾俼俠倧倐乯偲丄廔抜壓懁偵斾傋偢偭偲崅偄埵抲偵偁傞偼偢丄偲巚偭偰偄偨偺偱偁傞丅
偑丄偙傟偼丄僄儈僢僞僼僅儘傾偱偼壗屘俠倧倐偺儈儔乕岠壥偑惗偠側偄偺偐偺棟孅傪峫偊偢偵丄偨偩寢壥揑偵惗偠傞揹埑偱尒傞偲僄儈僢僞僼僅儘傾偵婾偣傞偺偱丄僄儈僢僞僼僅儘傾偱偁傟偽儈儔乕岠壥偑惗偠側偄偐傜丄偲偄偆娫堘偭偨巚偄崬傒偩偭偨丅帺暘傕偁傑傝恖偺偙偲偼尵偊側偄傢側偀乮丱丱丟
偦傕偦傕儈儔乕岠壥偲偼丄俿俼偺俛亅俤娫乮俥俤俿側傜俧亅俽娫丄壗屘偙偙偐偲尵偊偽丄偳偺愙抧摦嶌偱傕丄恖偺搒崌偵傛傞暘椶偵偐偐傢傜偢丄慺巕偼偙偺俀抂巕娫偺怣崋偱摦嶌偟偰偄傞偺偩丅乯偵壛傢傞怣崋偑憹尭偟偨偲偒偵丄偙傟偵敽偄俛亅俠娫乮俧亅俢娫乯偺揹埑偑丄俛亅俤娫擖椡埵憡偲媡埵憡偱丄偐偮丄擖椡怣崋憹尭斾偺倃攞偺斾棪偱憹尭偡傞応崌偵惗偠傞尰徾偱偁傞丅
偄傢備傞僄儈僢僞僼僅儘傾摦嶌偺応崌偺擖椡偼儀乕僗偲傾乕僗娫偱偁傞丅偦偟偰丄儀乕僗亅傾乕僗娫偲俛亅俤娫偺擖椡揹埑憹尭斾棪偼傎傏侾丗侾偱偁傞丅僐儗僋僞偼岎棳揑偵傾乕僗偵愙抧偝傟偰偄傞偐傜丄怣崋偼俛亅俠娫偵擖椡偝傟傞偲尵偭偰傕椙偄栿偩丅偟偨偑偭偰擖椡偺憹尭斾偲丄偙傟偵敽偆俛亅俠娫偺揹埑憹尭斾偼屳偄偵媡憡偱偼偁傞偑斾棪偲偟偰偼侾丗侾偵偟偐側傜側偄丅偲偄偆偙偲偼偡側傢偪丄俛亅俤娫偲俛亅俠娫偺揹埑憹尭斾傕侾丗侾偵偟偐側傜側偄偺偱偁傞丅
廬偭偰偄傢備傞僼僅儘傾摦嶌偱偼儈儔乕岠壥偑敪惗偟側偄偺偩丅
偙傟偑偄傢備傞僄儈僢僞愙抧摦嶌偺応崌丄俿俼偺俛亅俤娫偵擖椡偑壛傢偭偨応崌丄俛亅俠娫偼偦偺憹尭偺俙乮僄儈僢僞愙抧偺応崌偺揹埑憹暆棪乯攞偺斾棪偱偟偐傕俛亅俤娫偲偼媡埵憡偱憹尭偡傞丅偙偺偨傔俛亅俠娫偺俠倧倐偑摍壙揑偵乮侾亄俙乯攞偵側傞偺偱偁傞丅
偱偼丄姰慡懳徧宆偺廔抜偺忋懁偼偳偆偩傠偆偐丅偦偺俛亅俤娫偲俛亅傾乕僗娫亖俛亅俠娫偺憹尭斾棪偑栤戣側偺偩偑丄側傫偲偦傟偼侾丗俙偲偄傢備傞僄儈僢僞愙抧偺応崌偲慡偔摨偠側偺偱偁傞丅偐偮丄俛亅俠娫偼俛亅俤娫偲媡埵憡偩丅廬偭偰丄姰慡懳徧宆偺廔抜忋懁偵偼壓懁偲摨條偵儈儔乕岠壥偑敪惗偟丄偦偺俠倧倐偼摍壙揑偵乮侾亄俙乯攞偵側傞偺偱偁傞丅慡偔僄儈僢僞愙抧偲摨條側偺偩丅僄儈僢僞愙抧偺応崌偼僐儗僋僞偺揹埵偑儀乕僗揹埵偲媡憡偱俙攞偱怳傟傞偺偱乮侾亄俙乯偵側傞偺偵懳偟偰丄姰慡懳徧宆偺忋懁偺応崌偼儀乕僗揹埵偑岎棳揑偵傾乕僗偱偁傞僐儗僋僞揹埵偵懳偟偰乮侾亄俙乯攞偱怳傟傞丄偲偄偆揰偑堘偆偲尵偊偽堘偆偑丄寢壥偼慡偔摨條偩丅
壗屘偙偆側傞偺偐丅偦傟偼揹棳婣娨偑妡偐傜側偄偐傜側偺偱偁傞丅揹棳僪儔僀僽偟偨偄傢備傞僄儈僢僞僼僅儘傾偼偦偺僄儈僢僞掞峈偵惗偠傞揹埑偵傛傞婣娨嶌梡偑摥偐側偄丅寢壥丄慡偔偄傢備傞僄儈僢僞愙抧偲摍壙側偺偩丅俀抜栚偑揹棳弌椡偱偁傞偙偲偑幚偵梫乮僇僫儊乯側偺偱偁傞丅斀懳偵俀抜栚傪揹埑弌椡偵偟偰揹棳婣娨偑妡偐傞傛偆偵偡傟偽丄偦傟偼偄傢備傞僄儈僢僞僼僅儘傾摦嶌偲側傝儈儔乕岠壥傕敪惗偟側偄偙偲偵側傞丅偑丄偦傟偱偼廔抜偼懳徧摦嶌偵偼側傜側偄丅傑丄偩偐傜偙偦姰慡懳徧宆偼俀抜栚偑揹棳弌椡側偺偩丅
偲尵偆傢偗偱丄偙偺寢壥丄姰慡懳徧宆偺廔抜偼帪掕悢傕姰慡偵懳徧側偺偱偁傞丅
偙偆偟偰尒傞偲偄傢備傞僄儈僢僞僼僅儘傾摦嶌傪偦偺揟宆摦嶌奣擮偱帵偝傟傞摦嶌偵偣偟傔偰偄傞傕偺偼揹棳婣娨偱偁傞丄偲偄偆偙偲偑椙偔暘偐傞丅僄儈僢僞懁偵擖偭偨掞峈偵揹棳婣娨偑惗偠偰偙偦偄傢備傞僼僅儘傾摦嶌側偺偱偁傞丅偲側傞偲丄偙傟傪柍帇偟偰丄揹棳僪儔僀僽偵傛傝揹棳婣娨偑妡偐傜側偄応崌偵偮偄偰傑偱丄偦傟傪僼僅儘傾摦嶌偵暘椶偡傞偙偲偼柍塿偩丅
傕偲傕偲僄儈僢僞乮僜乕僗乯愙抧偲僄儈僢僞乮僜乕僗乯僼僅儘傾偼摨堦偺傕偺偱偁傞丅偄傢備傞僄儈僢僞乮僜乕僗乯僼僅儘傾偲偄偆傕偺偼偙傟傪揹埑僪儔僀僽偟偨応崌偺摿庩椺偱偁傞丅偲偡傞偺偑丄慜抜偺摦嶌傕娷傔偰摦嶌傪椶宆壔乮掕媊乯偡傞応崌偺傛傝惓偟偄奣擮丄偲偄偆偙偲偵側傞偩傠偆丅
偝偰丄
偙傟偱姰慡懳徧宆偲偼丄弶抜丄俀抜栚丄廔抜偲傕偵丄棙摼丄埵憡偲傕姰帏偵堦抳偟偨俹俹摦嶌傪偡傞傾儞僾偱偁傞偙偲偑傛偆傗偔暘偐偭偨丅乮丱丱乯
乽崱崰傗偭偲暘偐偭偨偺偐偹丒丒丒乿偲丄揤偺惡丅丂偼偭丂倣乮丵丵乯倣
仜僎僀儞僐儞僩儘乕儖傾儞僾
姰慡懳徧宆偺乽姰慡懳徧乿偺堄枴傕暘偐偭偨丅
偙傟偱偙偺俶倧亅侾俇俉俥俙儌僨儖偺埵憡曗惓偵偮偄偰傕埨怱偟偰専摙偱偒傞丅
愭偢偼埵憡曗惓側偟偺応崌丅栜榑廔抜俠俋俆俋偺俠倧倐憐掕偺俠侾俉侾俆俛亅俠娫俁侽倫俥偼帪掕悢傪嶌傞丅忋偱寁嶼偟偨偲偍傝丄弌椡偵宷偄偩晧壸掞峈偑侾倠兌偺応崌丄倖們佮俋侽俲俫倸偩丅
偦偙偱丄晧壸掞峈傪侾倠兌丄俀倠兌丄係倠兌丄俉倠兌丄侾俇倠兌丄俁俀倠兌丄俇係倠兌偲俇倓俛僗僥僢僾偱憹壛偝偣偨応崌偺丄揹埑棙摼乮倓俛乯摿惈偲揹埑乮埵憡乯摿惈傪娤偰傒傞丅
忋懁偵偁傞偺偑弌椡揹埑偺埵憡偱偁傝丄忋偐傜晧壸掞峈侾倠兌丄俀倠兌丄係倠兌丄俉倠兌丄侾俇倠兌丄俁俀倠兌丄俇係倠兌偺応崌偱偁傞丅懳墳偡傞僌儔僼偺廲幉偼塃懁偺乽俀乿偺曽偱埵憡偑侽亱乣亅俇侽侽亱偲偄偆偙偲偱偁傞丅
壓懁偑弌椡揹埑偺棙摼偱丄偙偪傜偼忋偐傜晧壸掞峈俇係倠兌丄俁俀倠兌丄侾俇倠兌丄俉倠兌丄係倠兌丄俀倠兌丄侾倠兌偺応崌偱偁傞丅懳墳偡傞僌儔僼偺廲幉偼嵍懁偺乽侾乿偱扨埵偼倓俛偱偁傞丅
梊憐捠傝偺寢壥偩丅廔抜俿俼偺俠倧倐亖俁俀倫俥丄僪儔僀僽僀儞僺乕僟儞僗侾丏俁俆倠兌丄侾亄俙乮廔抜揹埑僎僀儞乯偺儈儔乕岠壥丂偵傛傝偙偺傾儞僾偺戞侾億乕儖偑宍惉偝傟偰偄傞丅
晧壸掞峈偑憹偊傞偺偲傎傏斾椺偟偰廔抜偺揹埑僎僀儞俙偑憹偊傞丅寢壥儈儔乕岠壥傕斾椺偟偰憹偊傞偺偱億乕儖傕斾椺偟偰掅堟偵壓偑傞丅
寢壥晧壸掞峈侾倠兌偱偺倖們佮俋侽倠俫倸丄俇係倠兌偱偼倖們佮俁倠俫倸偱偁傞丅
侾俵俫倸傑偱偼亅俇倓俛乛倧們倲偱揹埑棙摼偑尭悐偟偰偍傝丄偙傟偑戞侾億乕儖偱偁傞偙偲偼媈偄偑側偄丅
侾乣俀俵俫倸偲偄偆掅偄埵抲偵戞俀億乕儖偑尒傜傟傞偙偲丄偝傜偵偙傟埲忋偺崅堟偱偺埵憡夞揮偑懍偄偙偲丄偑栤戣偩丅
壗屘側傜丄偙偺僼儔僢僩傾儞僾偼僎僀儞僐儞儘乕儖傾儞僾偲偟偰晧壸掞峈抣偑偄偢傟偺応崌偱傕乮亖僋儘乕僘僪僎僀儞偵偐偐傢傜偢亖儃儕儏乕儉愝掕偑偳偙偵偁偭偰傕乯晧壸侾倠兌偺応崌偺僆乕僾儞僎僀儞抣亖係俆倓俛偲偄偆怺偄俶俥俛傪妡偗偰巊偆偐傜偩丅
僗僞僈乕斾傪尒偰傒傞偲戞俀億乕儖傪侾丏俉俵俫倸偲偟偰傕戞侾億乕儖偑俋侽倠俫倸偱偼侾俉侽侽乛俋侽亖俀侽偟偐側偄偺偩丅偙傟偱偼埨慡偵妡偗傜傟傞俶俥俛検偼俀侽乛俀亖侾侽攞亖俀侽倓俛傑偱偱偟偐側偄丅偳偺傛偆偵偟偰係俆倓俛傕偺怺偄俶俥俛傪妡偗傞偺偩傠偆偐丅
帋偟偵丄偙偺傑傑偺忬懺偱俶俥俛傪妡偗偰傒傛偆丅壓恾偺俼侾侾傪侽兌丄侾倠兌丄俁倠兌丄俈倠兌丄侾俆倠兌丄俁侾倠兌丄俇俆倠兌偲偟偨応崌偵僋儘乕僘僪僎僀儞偱偺摿惈偼偳偺傛偆偵側傞偩傠偆偐丅
栜榑忋偐傜俼侾侾偑俇俆倠兌丄俁侾倠兌丄侾俆倠兌丄俈倠兌丄俁倠兌丄侾倠兌丄侽兌偺応崌偱丄惓妋偵俁俇倓俛乣侽倓俛傑偱俇倓俛僗僥僢僾偲側偭偰偄傞丅
偙偺偄偢傟偺応崌偱傕棟憐揑偵偼俶俥俛検偑曄傢傜側偄丄偲偄偆偺偑僎僀儞僐儞僩儘乕儖傾儞僾偺堄枴偩丅忋偺懳墳偡傞僆乕僾儞僎僀儞偲堷偒嶼傪偟偰傒傞偲暘偐傞丅偑丄尰幚偵偼僆乕僾儞僎僀儞偺曽偑晧壸偑戝偒偄傎偳偵晧壸偵斾椺偟偨忋徃傛傝傕彫偝偔側偭偰偟傑偆偺偱丄晧壸偑戝偒偄応崌偺俶俥俛検偼晧壸偑彫偝偄応崌偺俶俥俛検傛傝嬐偐偵彫偝偔側傞丅偦偺尨場偼丄揹棳弌椡偲偄偭偰傕俀抜栚嵎摦傾儞僾傗廔抜偺弌椡僀儞僺乕僟儞僗偑柍尷戝偱偼側偄偐傜偱偁傞丅
偝偰丄栤戣偼梊憐捠傝俀侽倓俛埲壓偺僋儘乕僘僪僎僀儞愝掕偱惗偠傞侾俵俫倸挻偺崅堟偱偺僺乕僋偩丅
尰幚偺応崌丄偙傟偱偼敪怳偡傞丅
偱偼丄俀抜栚嵎摦傾儞僾偺椺偺埵抲偵埵憡曗惓俠傪擖傟傛偆丅偙偙偼宱尡忋傕旕忢偵嫮椡側岠壥傪敪婗偡傞埵憡曗惓売強偩丅
偲偙傠偑丒丒丒
偳偆傕嬶崌偑椙偔側偄丅侾侽侽倫俥側傫偰偲傫偱傕側偄悢抣傪擖傟偰傒偰傕丒丒丒
戞侾億乕儖偼俀抜栚嵎摦傾儞僾偵擖傟偨侾侽侽倫俥偺岠壥偱俆侽侽俫倸偐傜侾侾倠俫倸掱搙偵僌僢偲壓偑偭偨丅
偑丄偙傟偱傕俶俥俛傪妡偗傞偲僎僀儞侽倓俛偱偼崅堟偵戝偒側僺乕僋偑惗偠傞丅
偙傟偱傕懯栚偩丅
偱偼丄傕偲傕偲偺戞侾億乕儖丄廔抜俿俼偺俛亅俠娫偺俠傪憹傗偟偰偼偳偆偐丅
偙傟偵傛偭偰傕栜榑戞侾億乕儖偼戝暘掅堟偵壓偑傞偺偩偑丒丒丒
傗偼傝僺乕僋偑惗偠傞丅偙傟偱傕懯栚偺傛偆偩丅
僋儘乕僘僪僎僀儞侽倓俛偲偄偆偺偼傗偼傝擄偟偄丅
傕偆堦搙椙偔僆乕僾儞僎僀儞摿惈傪尒傛偆丅
栤戣偼僆乕僾儞僎僀儞偑侽倓俛偲側傞億僀儞僩偺埵憡側偺偩丅
偙傟傜偺埵憡曗惓偱偼丄僆乕僾儞僎僀儞偑侽倓俛偲側傞億僀儞僩偱偺埵憡梋桾偑夵慞偝傟偰偄側偄丅
偳傟傕亅侾俆侽亱埲忋偩丅
偙傟偱偼俶俥俛屻埨掕側傾儞僾偵偼側傜側偄丅
懳嶔傪曄偊傞昁梫偑偁傞丅
壗偲偐偟偰丄婃屌偵摦偐側偄侾俵俫倸挻晅嬤偺億乕儖偵傛傞埵憡夞揮傪抶傜偣傜傟側偄偩傠偆偐丠
偦傟偑壓偺弶抜偵擖傟偨僗僥僢僾宆埵憡曗惓偩丅
戞侾億乕儖偺掅壓傪偦傟傎偳彽偐偢偵丄侾俵俫倸晅嬤偱偺埵憡夞揮傪堷偒栠偟丄寢壥丄僆乕僾儞僎僀儞偑侽倓俛偲側傞億僀儞僩偱偺埵憡夞揮偑侾係侽亱偵廂傑偭偨丅
側傫偲愨柇側丅
偙傟側傜懡暘戝忎晇偩丅
姰慡懳徧宆僾儕傾儞僾丅
娙扨偦偆偵尒偊傞僼儔僢僩傾儞僾偺曽偑丄幚偼僀僐儔僀僓乕傾儞僾傛傝傛傎偳擄偟偄偺偩丅
乮俀侽侽俁擭侾寧俀俇擔乯
忋偺埵憡曗惓偺専摙偱丄俀抜栚嵎摦傾儞僾偺椺偺埵抲偵埵憡曗惓梡俠傪擖傟偰傒偨応崌偺寢壥偺僌儔僼偵偍偗傞揹埑棙摼摿惈偲埵憡摿惈偼丄偪傚偭偲恞忢偱偼側偄丅偲巚偊傞偺偩偑偳偆偩傠偆丅
傛偔尒偰梸偟偄丅
廔抜俿俼偺俠倧倐乮俠侾俉侾俆杮棃偺俀倫俥亄俛俠娫偵擖傟偨俁侽倫俥亖俁俀倫俥乯偵傛傝晧壸侾倠兌偺応崌偱廔抜擖傝岥偵弌棃傞偼偢偺栺俋侽倠俫倸偺億乕儖偺巔偑側偄偺偩丅偦偆丄億乕儖偑徚柵偟偰偟傑偭偰偄傞偺偱偁傞丅
偦傟偩偗偱偼側偄丅埵憡抶傟俋侽亱偺廃攇悢堟偑堎條偵挿偔懕偄偰偄傞偽偐傝偐丄侾侽侽倠俫倸埲忋偱偼埵憡偑侾侽亱掱搙尦偵栠偭偰偄傞偱偼側偄偐丅
偙傟偼偪偲丄偄傗丄偐側傝曄偱偡傛偹偉丒丒丒
戝懱丄廔抜偵俋侽倠俫倸偺億乕儖偑偁傞偲偄偆偙偲偱偁傟偽丄僗僞僈乕斾偺娭學偐傜偟偰丄偦偺慜抜偵偙傟偲嬤偄掅偄億乕儖側偳攝抲偱偒傞偼偢偑側偄丄偲偄偆偺偑恞忢側峫偊曽偩丅
偐偮偰偺俲幃偱偼侾侽倠俫倸乣俀侽倠俫倸掱搙偺戞侾億乕儖傪俀抜栚嵎摦傾儞僾偺偲偙傠偵攝抲偡傞偺偑捠椺偱偁偭偨偑丄偙偺傛偆偵廔抜偵俋侽倠俫倸偺億乕儖偑偁傞応崌偵偦偺傛偆側偙偲傪偟偨傜丄僗僞僈乕斾偼侾侽傕妋曐偱偒偢丄俶俥俛側偳妡偗傜傟側偄忬懺偵側偭偰偟傑偆偼偢偩丅柍棟偵傗傞偲偡傟偽丄戞侾億乕儖偼僆儁傾儞僾暲傒偵悢廫俫倸戜偵攝抲偟側偄偲偩傔偩丄偲峫偊傞偺偑晛捠偩傠偆丅偩偐傜丄僆儕僕僫儖俶倧亅侾俇俉偺埵憡曗惓偼弶抜偺僗僥僢僾宆偱懳張偟偰偄傞偺偩傠偆丄偲偄偆偙偲偵側傞傢偗偩丅
偩偑丄僔儈儏儗乕僔儑儞側偺偱姼偊偰傗偭偰傒偨偺偩偑丄偙偺応崌偼丄偛偔恞忢側峫偊曽偐傜偟偰丄偙偺僌儔僼偼傑偢俀抜栚嵎摦傾儞僾偺偲偙傠偵庢傝晅偗偨俠偵傛傞戞侾億乕儖偺偲偙傠偱棙摼僌儔僼偼亅俇倓俛乛倧們倲偱孹偒丄埵憡偼亅俋侽亱傊岦偗偰夞揮偟丄戞俀億乕儖偲側傞俋侽倠俫倸晅嬤偱棙摼僇乕僽偑亅侾俀倓俛乛倧們倲偲孹偒偑媫偵側傞偲偲傕偵丄埵憡傕亅侾俉侽亱傊岦偗偰夞揮偑懍偔側傞傕偺丄偲憐掕偟偰偄偨偺偱偁傞丅
側偺偵丄偙傟偼偳偆偟偨偙偲側偺偩傠偆丠丠丠
傑傞偱丄億乕儖徚柵儈僗僥儕乕偱偼側偄偐丒丒丒
妋偐傔傛偆丅
廔抜偺億乕儖傪偢偭偲崅堟偵堏摦偝偣丄俀抜栚嵎摦傾儞僾偺椺偺売強偵擖傟傞俠偱栺俋侽倠俫倸偵戞侾億乕儖傪敪惗偝偣偰傒傛偆丅
廔抜偺億乕儖偼奜晅偗偺俁侽倫俥傪庢傝奜偣偽丄俠倧倐偼慺巕杮棃偺俀倫俥偵側傞偺偱丄偙傟偵傛傞廔抜偺億乕儖偼晧壸掞峈侾倠兌偱丂
倖倧亖侾俆俋乛乮侾丏俁俆亊侽丏侽侽侽侽侽俀亊係侾乯佮侾丏係係俵俫倸丂偲側傞偼偢偱偁傞丅
偲偙傠偱丄姰慡懳徧宆偺俀抜栚偺慺巕偺俠倧倐傗俠倰倱倱偱帪掕悢偑敪惗偡傞儊僇僯僘儉偱偁傞偑丄偙傟偵偮偄偰偼丄俧俷俙宆摍偺応崌偲摨偠傛偆偵丄儈儔乕岠壥偱俠倧倐傗俠倰倱倱偑奼戝偝傟丄偙傟偑俀抜栚擖傝岥偺弶抜晧壸掞峈乮俀抜栚偑俿俼偱偁傞応崌偼偙傟偵俿俼偺擖椡僀儞僺乕僟儞僗偑僷儔偵側傞乯偲偱帪掕悢傪宍惉偡傞傕偺丄偲偄偆揰偵壗傜曄傢傝偼側偄丅
俀抜栚偼揹棳弌椡偱偼偁傞偑丄偦偺寢壥偲偟偰慺巕偺俛亅俠娫乮俧亅俢娫乯偺揹埑偼曄摦偟偰偄傞偐傜丄傕偲傕偲帪掕悢偼惗偠傞偟丄偙傟偑俛亅俤娫乮俧亅俽娫乯偺擖椡揹埑偲媡憡偱偐偮怳暆偑擖椡揹埑怳暆偺倃攞偱偁傟偽丄儈儔乕岠壥偱俠倧倐傗俠倰倱倱偑乮侾亄倃乯攞偵摍壙揑偵奼戝偝傟傞偲偄偆揰傕摨偠側偺偱偁傞丅
偦偙偱丄俀抜栚偵惗偠傞帪掕悢傪寁嶼偡傞偨傔偵偼丄俀抜栚偵擖傟傞俠偺椉抂揹埑偺怳暆斾偑壗攞側偺偐偑柧傜偐偱偁傞昁梫偑偁傞偺偩偑丄偦傟偼丄弶抜偺揹埑僎僀儞偲俀抜栚亄廔抜偺揹埑僎僀儞偺攞棪偦偺傕偺側偺偱偁傞丅
偨偩偟丄偙偺応崌偵嵎摦傾儞僾偺塃懁偼偙偺偲偍傝弶抜揹埑僎僀儞丗俀抜栚揹埑僎僀儞亊廔抜揹埑僎僀儞丂偱偁傞偑丄嵎摦傾儞僾嵍懁偼弶抜揹埑僎僀儞丗俀抜栚揹埑僎僀儞丂偱偁傞丅廔抜偺揹埑僎僀儞暘偑俀抜栚偺塃懁偩偗偵棙偄偰偔傞栿偱丄偙偺偨傔塃懁偺椺偺応強偵俠傪擖傟傞偲儈儔乕岠壥偑廔抜偺僎僀儞暘戝偒偔側傞偺偱偁傞丅
偱丄埲壓偼俀抜栚塃懁偵埵憡曗惓傪擖傟傞偙偲傪憐掕偟偨傕偺偱偁傞丅
偡偱偵夝愅偟偨偲偍傝丄弶抜丄俀抜栚嵎摦傾儞僾丄廔抜偺揹棳僎僀儞丄揹埑僎僀儞偼偙偆偩丅
丂丂丂丂丂丂丂丂丂弶抜丂丂丂丂丂俀抜栚丂丂丂丂丂丂廔抜乮俹俹摦嶌偱乯丂丂丂丂丂寁
揹棳僎僀儞丂丂丂侾丏侾倣俽丂丂丂侾丏俇俈倣俽丂丂丂丂丂俆俁丏侾俇攞丂丂丂丂侾俈俈倣俽丂丂丂乮倗倣昞帵乯
揹埑僎僀儞丂丂丂侾丏侾倣俽丂丂丂俁丏俁俁倣俽丂丂丂丂丂丂侾俈俈倣俽丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂亊侾丏俉倠兌丂丂亊侾丏俁俆倠兌丂丂亊丂丂丂丂丂侾倠兌丂丂丂亊丂丂侾倠兌丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乛侾丏俋俉丂丂丂丂乛丂丂丂係丏俆
揹埑僎僀儞丂丂佮侾丏俋俉攞丂丂佮俀丏俀俈攞丂丂丂佮丂丂丂俁俋丏俆攞丂丂丂丂侾俈俈攞
丂丂丂丂丂丂丂丂乮俀攞乯丂丂丂丂乮俀丏俀攞乯丂丂丂丂丂丂丂乮係侽攞乯丂丂丂亖係俆倓俛
丂丂丂仏拲乯丂偙偙偱廔抜偺揹埑僎僀儞偼廔抜偺晧壸掞峈偵斾椺偟偰曄摦偡傞丅
寁嶼偺曋媂忋丄揹埑僎僀儞丂弶抜亖俀攞丄俀抜栚亖俀丏俀攞丄廔抜亖係侽亊晧壸乮倠兌乯攞偲偟傛偆丅
偲偡傞偲丄廔抜俿俼偺俛亅俤偲俛亅俠娫偺揹埑憹尭斾棪偑係侽亊晧壸乮倠兌乯攞偱丄俀抜栚俥俤俿偺俧亅俽偲俧亅俢娫偺揹埑憹尭斾棪偑俉俉乮係侽亊俀丏俀乯亊晧壸乮倠兌乯攞偲偄偆偙偲偱偁傞偐傜丄
廔抜俿俼偵摥偔儈儔乕岠壥偼丄丂丂丂侾亄係侽亊晧壸乮倠兌乯丂攞
俀抜栚俥俤俿偵摥偔儈儔乕岠壥偼丂丂侾亄俉俉亊晧壸乮倠兌乯丂攞
寢壥
廔抜擖傝岥偵弌棃傞億乕儖偼丂丂fo亖侾俆俋乛乮侾丏俁俆亊俠倧倐亊乮侾亄係侽亊晧壸乯乯
俀抜栚擖傝岥偵弌棃傞億乕儖偼丂fo亖侾俆俋乛乮侾丏俉亊俠倰倱倱亊乮侾亄俉俉亊晧壸乯乯
偲寁嶼偝傟傞偙偲偵側傞丅
晧壸侾倠兌偱廔抜俿俼俠倧倐亖俁俀倫俥偩偲丂廔抜億乕儖fo亖俉俋丏俉倠俫倸偼忋偱寁嶼偟偨偲偍傝偩丅
偱丄晧壸侾倠兌偱俀抜栚嵎摦傾儞僾偺椺偺売強偵侾侾倫俥偺俠傪奜晅偗偡傞偲丄寁嶼忋俀抜栚偵fo亖俋侽倠俫倸偺億乕儖偑偱偒傞偼偢丄偲偙偺寁嶼幃偐傜媮傔傜傟傞丅偺偱丄偙傟傪尒偰傒傛偆丅
寢壥丄妋偐偵俋侽倠俫倸偵戞侾億乕儖偑弌棃偰偄傞丅偙傟偼俀抜栚偵弌棃偨億乕儖偩丅廔抜偺億乕儖傪偼偠傔戞俀億乕儖埲崀偼俵俫倸埲崀偵偁傞丅
斾妑偺偨傔偵丄俀抜栚偺俠傪庢傝嫀傝丄廔抜偵俁侽倫俥傪奜晅偗偟偰廔抜偱俋侽倠俫倸偺戞侾億乕儖傪嶌偭偨応崌傕尒偰偍偙偆丅
偙傟偱傕栜榑栺俋侽倠俫倸偺戞侾億乕儖傪嶌傟傞傢偗偩丅栜榑俀抜栚偱嶌偭偨応崌偲偼旝柇側堘偄偼偁傞丅偦傟偼摉慠偩丅
偝偁丄偱偼廔抜偱弌棃傞億乕儖偼偙偺傑傑偵偟偰丄俀抜栚嵎摦傾儞僾偺椺偺埵抲偵侾侾倫俥傪奜晅偗偟丄俀抜栚偺億乕儖傕傢偞偲fo佮俋侽倠俫倸偺億僀儞僩偵傇偮偗偰傒傛偆偱偼側偄偐丅
fo亖俋侽倠俫倸偐傜棙摼偼亅侾俀倓俛乛倧們倲偺孹幬偱尭悐偟丄埵憡傕亅侾俉侽亱傊岦偗偰媫寖偵夞揮偟偰偟傑偆偼偢偩丅
偲偄偆梊憐偼慡偔奜傟丄栺俆侽倠俫倸偺戞侾億乕儖偑傂偲偮偱偒偨丅乮丠丠乯
棙摼偺壓崀捈慄偑侾俵俫倸挻傑偱亅俇倓俛乛倧們倲偱偁傞偟丄埵憡偺夞揮嬶崌偐傜偟偰傕侾俵俫倸晅嬤傑偱偼侾偮偺億乕儖偱偁傞丄偲偟偐撉傔側偄寢壥偩丅
側傫偲俋侽倠俫倸晅嬤偺俀偮偺億乕儖偑徚柵偟偰俆侽倠俫倸晅嬤偵怴偨偵侾偮偺億乕儖偑嶌傜傟偨丒丒丒丠丂偦傫側僶僇側両丂偑丄偙傟偑帠幚側偺偱偁傞丅
偄偐偑偩傠偆偐丅
偙傟偑丄幚偼億乕儖偑俀屄側偺偵侾屄偵偟偐尒偊側偄偲偄偆丄楢惎岠壥偺堦椺側偺偱偁傞丅
姰慡懳徧摦嶌丄偲偄偆傛傝丄廔抜偑偄傢備傞僄儈僢僞愙抧摦嶌偱揹埑僎僀儞傪帩偭偰偄傞偙偲偵傛偭偰丄俀抜栚偺億乕儖偲廔抜偺億乕儖偵乬楢惎岠壥乭偑惗偠傞偺偩丅
楢惎岠壥
丒幚偼億乕儖偑俀屄側偺偵帪偵侾屄偵偟偐尒偊側偄丅
丒偩偑丄侾屄偱偼偲偰傕偁傝偊側偄偺條憡傪帵偡丅
丒傛偔傛偔娤嶡偡傞偲幚偼俀屄偑偦傟偧傟塭嬁偟偁偭偰偦傫側晄巚媍側條憡傪帵偟偰偄傞偙偲偑暘偐傞丅
偲偄偆栿側偺偩丅
栤戣偼丄壗屘丄楢惎岠壥偑惗偠傞偺偐丠
側偺偩偑丄偦偺摎偊偼愭偺幃
廔抜擖傝岥偵弌棃傞億乕儖偼丂丂fo亖侾俆俋乛乮侾丏俁俆亊俠倧倐亊乮侾亄係侽亊晧壸乯乯
俀抜栚擖傝岥偵弌棃傞億乕儖偼丂fo亖侾俆俋乛乮侾丏俉亊俠倰倱倱亊乮侾亄俉俉亊晧壸乯乯
偵塀偝傟偰偄傞丅
栤戣偼廔抜偺揹埑棙摼側偺偱偁傞丅偦傟偼晧壸侾倠兌偺帪偵係侽攞偩丅偙傟偲俀抜栚偺揹埑棙摼偑壛嶼偝傟偰俀抜栚偺億乕儖傪寁嶼偡傞悢抣偼俉俉攞偵側傞丅
偑丄偙偺係侽攞偺棙摼偼廔抜偺掅堟偱偺棙摼偱偁傝丄廃攇悢偑崅偔側傞偲嫟偵廔抜偵弌棃傞億乕儖偵傛傝掅壓偟偰偄偔丅偙傟偼摉慠偺寢壥偱偁偭偰廔抜偺億乕儖帺懱偺巔偵偼壗偺摿暿側塭嬁傪梌偊傞傕偺偱偼側偄丅
偑丄俀抜栚偺億乕儖偺宍惉偵偼戝偒側塭嬁傪梌偊傞偺偱偁傞丅廔抜偺棙摼偑帺傜偺億乕儖偱掅壓偟偰偟傑偆偲丄忋偺幃偱晧壸侾倠兌偺応崌偺乽俉俉乿偺悢帤偑摉慠尭偭偰偄偔偺偱偁傞丅偙傟偼俀抜栚偵惗偠傞儈儔乕岠壥傪尭彮偝偣傞偲偄偆偙偲偩丅
姰慡懳徧宆偺応崌丄俀抜栚偵弌棃傞億乕儖偼栜榑廔抜偺僎僀儞偺娭悢側偺偱偁傞偑丄廔抜偺僎僀儞偼廔抜帺懱偺億乕儖偵傛偭偰廃攇悢偺娭悢偱偁傞丅偙偺偨傔丄俀抜栚偵弌棃傞億乕儖偼帺傜偺俠偵傛傞廃攇悢偺娭悢偱偁傞偩偗偱偼側偔丄廔抜偺億乕儖偵傛傞廃攇悢偺娭悢偱傕偁傞丄偲偄偆偙偲側偺偱偁傞丅偦偟偰丄俀抜栚偺億乕儖偵摥偔廔抜億乕儖偵傛傞廃攇悢偺娭悢偼帺傜偺俠偵傛傞廃攇悢娭悢偲岠壥偑媡側偺偩丅偡側傢偪屳偄偵懪偪徚偟崌偆儀僋僩儖側偺偱偁傞丅
偩偐傜丄忋偺傛偆偵擇偮偺億乕儖傪傇偮偗傞偲丄侾偮偺億乕儖偑徚柵偟偰偟傑偭偨傛偆側寢壥偵側傞偺偱偁傞丅
姰慡懳徧宆偼丄偙偺楢惎岠壥乮佮億乕儖偺懪偪徚偟岠壥乯偺偨傔偵俀抜栚偺億乕儖偲廔抜偺億乕儖偼偛偔嬤偔偵偁偭偰傕丄偁傞偄偼廳側偭偰偄偰傕壗傜栤戣偑側偄偺偱偁傞丅媡偵偙偺岠壥傪忋庤偔妶梡偡傞偙偲偵傛偭偰埵憡曗惓偵慺惏傜偟偄岠壥傪惗傒弌偡偙偲傕壜擻偐傕抦傟側偄傎偳偩丅
暘偐偭偰偟傑偊偽摉偨傝慜偺偙偲側偺偩傠偆丅
忢幆偩偗偱側偔婛抦偺奣擮偐傜側偐側偐敳偗弌偣側偄偺偑杴恖偺杴恖偨傞偲偙傠偱偁傞亜乮丱丱丟
偙傟傪抦偭偰丄俶倧亅侾俁俋傪偁傜偨傔偰尒偰傒傞偺偱偁偭偨丒丒丒丅
俀抜栚嵎摦傾儞僾偲廔抜僪儔僀僶乕偵俠倧倐偺戝偒側俿俼傪婲梡偟偰偄偰傕丄楢惎岠壥偱僗僞僈乕斾偑庢傟側偄偲偄偆栤戣傕側偔乮幚偼偙傟偑晄巚媍偩偭偨偺偩乯丄幚幙揑偵侾億乕儖偺傛偆偵俶俥俛埨掕惈偺椙偄傾儞僾偵側偭偰偄偨傢偗偩丅
乬楢惎岠壥乭偺偄偔偮偐偺巔傪尒傞丅
廔抜億乕儖傪屌掕偟偨傑傑丄俀抜栚偺億乕儖傪偦偺屻傠偐傜慜偵堏摦偝偣傞丅
俀抜栚偺椺偺埵抲偵擖傟傞俠傪0p俥,1p俥,2p俥,4p俥,8p俥,16p俥,32p俥,64p俥,128p俥,256p俥偲曄偊偰偄偔僷儔儊僩儕僢僋夝愅
埵憡嬋慄偑塇偺傛偆側巔傪昤偔丅俀抜栚偺億乕儖偑慜曽偵堏峴偡傞傎偳偵埵憡偺栠傝岠壥偑尠挊偵側偭偰偄傞丅
廔抜偺億乕儖傪侾寘崅堟偵忋偘偰摨條偵梀傫偱傒傞丅
岠壥偼摨偠偩偑丄傛傝梇戝側巔偵側偭偨丅
崱搙偼俀抜栚偺億乕儖傪俋侽俲俫倸晅嬤偵屌掕偟偰丄廔抜偺億乕儖傪屻傠偐傜慜傑偱堏摦偝偣傞丅
恾偺俠俀亖侾倫俥丄俀倫俥丄係倫俥丄俉倫俥丄侾俇倫俥丄俁俀倫俥丄俇係倫俥丄侾俀俉倫俥偲曄壔偝偣偨僷儔儊僩儕僢僋夝愅
廔抜偺億乕儖偺堏摦偼弶抜偺億乕儖偺堏摦傕傕偨傜偟丄傑傞偱棙摼摿惈偼侾億乕儖偱丄埵憡摿惈偼俀億乕儖偑楢摦偟偰摦偄偰偄傞丄偲偄偭偨姶偠偺曄壔傪帵偡丅偲偰傕俀偮偺億乕儖偑嬤偯偄偰岎傢偭偰丄偲偄偆僀儊乕僕偱偼側偄丅
楢惎岠壥側偺偩丅
晄壜巚媍側悽奅側偺偩偑丄峫偊偰傒傟偽摉慠側偺偩傠偆丅
乮俀侽侽俁擭侾寧俀俋擔乯
楢惎岠壥偺尨場傪偝傜偵扵偭偰傒傞丅
俀抜栚偺俧亅俢娫偺俠偱埵憡曗彏偡傞偲丄俠偵傛傞婣娨嶌梡偱俀抜栚僇僗僐乕僪弌椡偑揹棳弌椡忬懺偐傜揹埑弌椡忬懺傊偲堏峴偡傞偺偱偼側偐傠偆偐丅偦偆偡傞偲廔抜忋懁偼僄儈僢僞愙抧摦嶌偐傜僄儈僢僞僼僅儘傾摦嶌偵堏峴偟偰偟傑偆偼偢偩丅僄儈僢僞僼僅儘傾摦嶌偱偁傟偽廔抜偵偼儈儔乕岠壥偑惗偠側偄丅偩偐傜廔抜偺儈儔乕岠壥偼徚柵偡傞丅
偙傟偑楢惎岠壥偺幚懱側偺偱偼側偄偩傠偆偐丅
妋偐傔傛偆丅
帠幚傪妋幚偵娤應偡傞偨傔偵丄俀抜栚偼憡屳嶌梡偑惗偠側偄傛偆嵎摦傾儞僾傪巭傔偰撈棫偺僜乕僗愙抧摦嶌偵偡傞丅
廔抜忋懁偩偗偵埵憡曗惓梡偺俠侾侽侽倫俥傪憓擖偡傞丅
偝傜偵廔抜傕忋壓傪暘棧偟憡屳嶌梡傪攔彍偡傞丅
偙偺忬懺偱俬倁曄姺掞峈偱偁傞俼俉偲俼俋偺椉抂揹埑丄媦傃丄忋懁偺晧壸俼侾俆偲壓懁偺晧壸俼侾俇偺椉抂揹埑傪娤應偡傞丅
廔抜壓懁偼俀抜栚偺弌椡偑揹棳弌椡偱偁傠偆偑揹埑弌椡偱偁傠偆偑僄儈僢僞愙抧摦嶌傪偡傞偑丄廔抜忋懁偼俀抜栚弌椡偑揹埑弌椡偵側偭偰偟傑偆偲妋偐偵僄儈僢僞愙抧摦嶌偐傜僄儈僢僞僼僅儘傾摦嶌偵側偭偰偟傑偆偼偢偩丅偦偆偡傞偲廔抜忋懁偲廔抜壓懁偺僎僀儞偼摉慠堎側傞偙偲偵側傞偐傜丄俼侾俆偲俼侾俇偵弌椡偝傟傞揹埑偵傕戝偒側嵎偑惗偠傞偩傠偆丅偦偺曈傪偙傟偱妋偐傔偰傒傛偆偲偄偆栿偩丅
寢壥偑壓偺僌儔僼丅
杴椺偵偁傞偲偍傝側偺偩偑丄侾俵俫倸晅嬤傑偱懷堟偑悈暯偵怢傃偰偄傞俀杮偺慄偺偆偪丄忋偑俼俋偺椉抂揹埑丄壓偑俼侾俇偺椉抂揹埑偺廃攇悢摿惈偱偁傝丄侾侽俲俫倸晅嬤偐傜婛偵壓崀偟偰偄傞慄偑幚偼俀杮傄偭偨傝偲廳側偭偰偄偰丄侾俆俵俫倸晅嬤偱暘偐傟偰忋偵怢傃偰偄偭偰偄傞偺偑俼俉偺椉抂揹埑丄懠曽偑俼侾俆偺椉抂揹埑偺廃攇悢摿惈偱偁傞丅
偨偩偟丄俼俉偲俼俋偺廲幉偼侾偺倣倁偺僗働乕儖偱偁傝丄俼侾俆偲俼侾俇偺廲幉偼俀偺倁偺僗働乕儖偱偁傞丅
俼俉偲俼俋偺椉抂揹埑偼掅堟偱俁係俈倣倁偲懳徧偱偁傞偑丄俀抜栚塃懁偵偼弶抜偺侾丏俉俲兌偲俠俁亖侾侽侽倫俥偵傛傞栺係俆俲俫倸偺帪掕悢偑惗偠偰偄傞偨傔偵侾侽俲俫倸庛偐傜揹埑偑掅壓偟偰偄傞偙偲偑暘偐傞丅
栤戣偼俼侾俆偲俼侾俇偵惗偠傞揹埑偩偑丒丒丒丅傕偟丄廔抜忋懁偑偄傢備傞僄儈僢僞僼僅儘傾摦嶌偵側偭偰偟傑偊偽揹埑憹暆擻椡偼幐傢傟傞偐傜丄僄儈僢僞愙抧摦嶌傪偡傞廔抜壓懁偲摨掱搙偺弌椡揹埑偵偼側傜側偄偼偢偩丅
偑丄
偙偺僌儔僼偺偲偍傝丄廔抜壓懁偺俼侾俇偺椉抂揹埑偑掅堟俇丏俈倁偱俼俋椉抂揹埑偺廃攇悢摿惈偲憡帡偱偁傞偺偲摨條偵丄廔抜忋懁偺俼侾俆偺椉抂揹埑傕掅堟俇丏俋係倁偱俼俉椉抂揹埑偲侾侽俵俫倸挻偺椞堟傑偱憡帡宍傪曐偭偨廃攇悢摿惈偲側偭偰偄傞丅
梫偡傞偵偙偺寢壥偼丄俀抜栚偵埵憡曗惓梡偺俠傪擖傟偰傕廔抜忋懁偼側偍揹埑僎僀儞傪桳偡傞僄儈僢僞愙抧摦嶌傪偟偰偄傞偲偄偆偙偲傪昞偟偰偄傞偺偱偁傞丅
偙偺寢壥偐傜偼丄埵憡曗惓俠偺憓擖偵傛傝俀抜栚偑揹埑弌椡乮亖掅弌椡僀儞僺乕僟儞僗乯偲側傝丄寢壥廔抜偑僄儈僢僞僼僅儘傾摦嶌偵側傞偨傔偵廔抜偺俠倧倐偵傛傝宍惉偝傟傞帪掕悢偑徚柵偡傞偙偲偑楢惎岠壥偺撪梕偱偁傞丄偲偄偆偙偲偵偼側傜側偄傛偆偩丅
廔抜俿俼偺俛亅俠娫偵侾侽侽倫俥傪憓擖偟偰傢偞偲廔抜擖傝岥偵傕栺俆侽俲俫倸偺帪掕悢偑惗偠傞傛偆偵偡傞丅
侾侽侽倫俥偺憓擖偵傛傝栺俆侽俲俫倸偵帪掕悢偑惗偠偰偄傞偺偑塃懁偺俀杮偺慄偱丄偙傟偑壓懁偱偁傞丅
廔抜忋懁偼壓偺嵍懁偺慄偱俀杮偑廳側偭偰偄偰侾杮偵偟偐尒偊側偄丅偑丄廲幉偺僗働乕儖偼忋偺応崌偲摨條偵暿乆偱偁傞丅
忋懁偺帪掕悢偼壓懁偺帪掕悢傛傝傗傗掅偄埵抲偵側傞丅偺偼偙傟傕楢惎岠壥偵傛傞傕偺偱偁傞丅
偟偐傕棙摼偺尭悐搙偼忋懁傕壓懁偲摨條亅俇倓俛乛倧們倲偺傑傑偱偁傞丅
廔抜傕偙偺忬嫷偱揹埑棙摼傪桳偟偰偄傞偙偲偼柧傜偐偱偁傝乮俙亖俇丏俋係倁乛俁係俈倣倁亖俀侽攞亖俀俇倓俛乯丄偱偁傟偽寁嶼忋傕侾俆俋乛乮侾丏俇乮俲兌乯亊侽丏侽侽侽侾乮倳俥乯亊俀侾乯佮係俈俲俫倸偺帪掕悢偑徚柵偡傞偙偲側偔惗偠偰偄傞偼偢偱偁傞丅
偑丄俀抜栚偵惗偠偰偄傞帪掕悢偲憡娭偟偰栺俀俆俲俫倸偺帪掕悢偑侾屄偩偗惗偠偰偄傞傛偆側條憡傪帵偟偰偄傞偺偩丅
傗偼傝丄俀抜栚俧亅俢娫偵憓擖偟偨俠偵傛傞婣娨嶌梡偱俀抜栚偺弌椡僀儞僺乕僟儞僗偑壓偑傝丄寢壥廔抜偑僄儈僢僞僼僅儘傾摦嶌偵側傞偨傔偵丄廔抜偺俠倧倐偵傛傝宍惉偝傟傞帪掕悢偑徚柵偡傞丄偙傟偑楢惎岠壥偺撪梕偱偁傞丄偲偄偆偙偲偱偼側偄傛偆偩丅
俀抜栚傪僄儈僢僞愙抧摦嶌偵偪傚偭偲曄偊偨偩偗偺傛偆偩偑丄偦傟偱偼俀抜栚偵嫮椡側揹棳婣娨偑妡偐偭偰棙摼傕廃攇悢摿惈傕戝暆偵曄傢傞偩傠偆偵丅忋偺寢壥偼偦偺偣偄偠傖側偄偐丒丒丒乮亅亅乯
偲丄巚傢傟傞曽傕偄傜偭偟傖傞偐傕偟傟側偄丅偺偱丄俀抜栚傪嵎摦傾儞僾偵栠偟偰摨條偵帋偟偰傒傞丅
妋偐偵偙傟偱俀抜栚偺揹埑僎僀儞偼忋偺侾侽攞嫮偵側傞丅
傛偭偰俀抜栚俧亅俢娫偵擖傟傞俠偼侾侽倫俥偵偡傞丅
寢壥偼丒丒丒丄摨偠偱偁傞丅
偦傟傛傝傕丄偙傟偱俀抜栚嵎摦傾儞僾偺擻椡偲偦偺尷奅偑暘偐傞丅
俀抜栚俧亅俢娫偺埵憡曗惓俠偼塃懁乮亖廔抜忋懁乯偵偟偐擖傟偰偄側偄偺偩偑丄偙傟偵傛偭偰惗偠偨帪掕悢偺岠壥偼俀抜栚嵍懁亖廔抜壓懁傕婯掕偟偰偄傞丅偙傟偑忋偺俀抜栚傪暘棧偟偨応崌偲偺堘偄偱偁傝丄偙傟偑嵎摦傾儞僾偲偟偰俹俹摦嶌偟偰偄傞徹嵍側偺偩丅
偑丄偦傟傜偼姰慡偵偼堦抳偟偰偄側偄丅偙偺揰偼俀抜栚嵎摦傾儞僾偺擻椡偺尷奅偩丅偙傟偼俀抜栚嵍懁偵傕揔愗側俠傪憓擖偡傞偙偲偵傛傝夵慞壜擻偐傕偟傟側偄丅
廔抜俿俼偺俛亅俠娫偵傕俠傪憓擖偟帪掕悢傪敪惗偝偣偰傒傞丅
侾侽侽俲俫倸掱搙偩偐傜俆侽倫俥偱椙偄偩傠偆丅
寢壥偼丄傗偼傝俀抜栚暘棧偺僄儈僢僞愙抧偺応崌偲摨偠偩丅
偙偺応崌偼廔抜擖傝岥偵敪惗偝偣偨帪掕悢偑儊僀儞億乕儖偵側偭偨傛偆偱丄偙偺曽偑偐偊偭偰忋壓偺僶儔儞僗偑椙偄偙偲偑暘偐傞丅巊偊傞寢壥偩丅
乮俀侽侽俁擭俁寧侾擔乯