《基　本　統　計　学　8》

　　　　●標準偏差　Ｓｔａｎｄａｒｄ　Ｄｅｖｉａｔｉｏｎ
　　　　　　　　　Ｓｔｄ、ｓ、σ

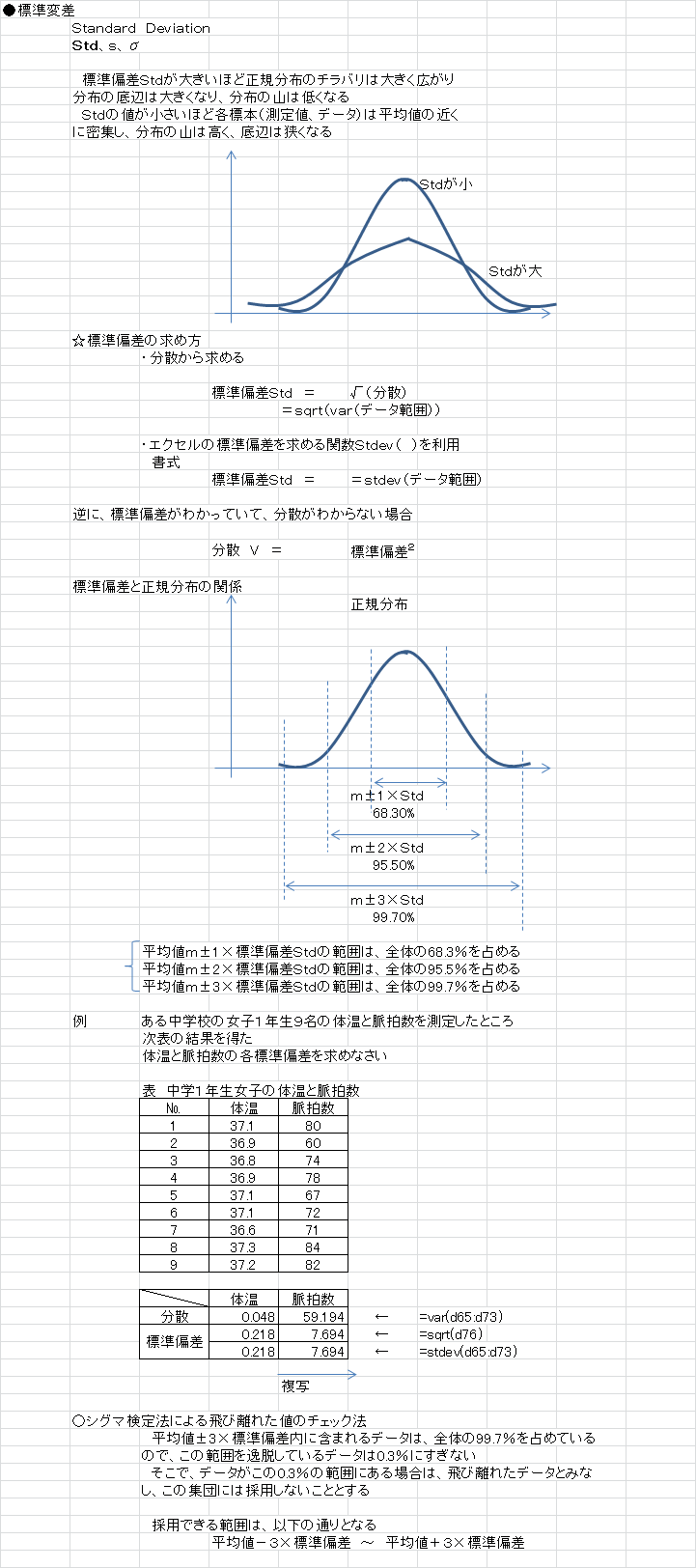
　　　　　　Ｓｔｄの値が大きい程、データのチラバリは大きく広がり、分布（正規分布）の底辺は広がる。
　　　　　　Ｓｔｄの値が小さい程、各標本（測定値）は平均値の近くに密集し、分布の底辺は狭くなる。

　　　　　　☆標準偏差の求め方
　　　　　　　　　　　標準偏差Ｓｔｄ　＝　√（分散）

　　　　　　　　　エクセルの標準偏差を求める関数を利用する場合
　　　　　　　　　　　標準偏差　＝ｓｔｄｅｖ（データ範囲）

　　　　　　　　　逆に、標準偏差が分っていて分散が分らない場合
　　　　　　　　　　　分散　＝　標準偏差２

　　　　　標準偏差と正規分布の関係
　　　　　　　　　平均値ｍ ± １ × 標準偏差Ｓｔｄ　の範囲は、全体の６８．３％を占める

　　　　　　　　　平均値ｍ ± ２ × 標準偏差Ｓｔｄ　の範囲は、全体の６８．３％を占める

　　　　　　　　　平均値ｍ ± ３ × 標準偏差Ｓｔｄ　の範囲は、全体の９９．７％を占める

　　　　　○シグマ検定法による飛び離れた値のチェック法
　　　　　　　　平均値±３×標準偏差内に含まれるデータは、全体の９９．７％を占めているので、その範囲を逸脱しているデー
　　　　　　　タは全体の０．３％すぎない。
　　　　　　　　そこで、データがこの０．３％の範囲にある場合は、飛び離れたデータとみなして、この集団には採用しない。
　　　　　　　　採用できるデータ範囲は、以下の通りです。

　　　　　　　　　　平均値 − ３ × 標準偏差　〜　平均値 ＋ ３ × 標準偏差

         　　　詳細は下図を参照