乻僂丂傿丂儖丂僐丂僋丂僗丂儞丂偺丂晞丂崋丂晅丂弴丂埵丂専丂掕乼
丂丂僨乕僞偺攚屻偵偁傞曣廤抍偺暘晍偑摿掕偱偒側偄応崌傪懳徾偲偡傞丅
丂丂丂仠僂傿儖僐僋僗儞偺弴埵榓専掕
丂丂丂丂丂僂傿儖僐僋僗儞偺弴埵榓専掕偼丄2偮偺廤抍娫偱乽懳墳娭學偑柍偄乿応崌偵丄偙偺2偮偺廤抍娫偵桳堄側嵎偑桳傞偐偳偆
丂丂丂丂丂偐傪専掕偡傞応崌偵梡偄傞丅
丂丂丂丂丂椺
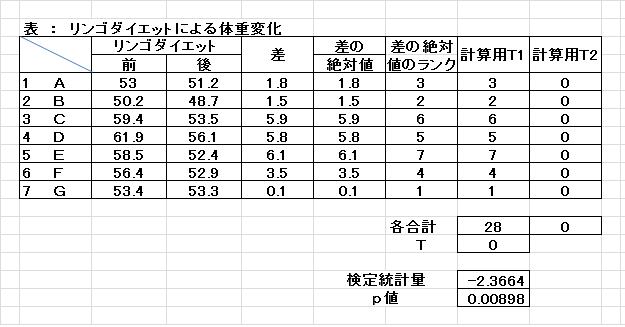
丂丂丂丂丂丂師偺僨乕僞偼丄7恖偺彈惈偺儕儞僑僟僀僄僢僩偵傛傞懱廳曄壔傪挷傋偨帒椏偱偡丅
丂丂丂丂丂丂偙偺僨乕僞偐傜丄儕儞僑僟僀僄僢僩偵傛偭偰懱廳偵桳堄側嵎偑惗偠偨偐偳偆偐傪専掕偟側偝偄丅
丂丂
 丂丂丂丂丂
丂丂丂丂丂寢壥
丂丂丂丂丂丂椉懁専掕偱偁傞偺偱
丂丂丂丂丂丂2亊倫抣亖0.00898亊2亖0.01796亙0.05丂偱偁傞偺偱婣柍壖愢俫0傪婞媝偟偰懳棫壖愢俫1傪嵦戰偡傞丅
丂丂丂丂丂寢榑
丂丂丂丂丂丂偡側傢偪丄桳堄悈弨5亾偵偍偄偰儕儞僑僟僀僄僢僩慜屻偱桳堄側嵎偑桳傞偙偲偑傢偐傞丅丂丂丂
丂丂丂丂丂丂儕儞僑僟僀僄僢僩偼桳岠偱偁傞偲寢榑晅偗傜傟傞丅
丂丂
丂丂丂仠僂傿儖僐僋僗儞偺晞崋晅弴埵専掕
丂丂丂丂丂僂傿儖僐僋僗儞偺晞崋晅弴埵専掕偼丄2偮偺廤抍娫偱乽懳墳娭學偑桳傞乿応崌偵丄偙偺2偮偺廤抍娫偵桳堄側嵎偑桳傞偐
丂丂丂丂丂偳偆偐傪専掕偡傞応崌偵梡偄傞丅
丂丂丂丂丂椺
丂丂丂丂丂丂嶐擭偲崱擭偺俀夞丄摨堦恖暔偵侾偐寧偺彂愋峸擖戙偵娭偡傞傾儞働乕僩傪幚巤偟偨偲偙傠師昞偺寢壥傪摼偨丅
丂丂丂丂丂
丂丂丂丂丂寢壥
丂丂丂丂丂丂椉懁専掕偱偁傞偺偱
丂丂丂丂丂丂2亊倫抣亖0.00898亊2亖0.01796亙0.05丂偱偁傞偺偱婣柍壖愢俫0傪婞媝偟偰懳棫壖愢俫1傪嵦戰偡傞丅
丂丂丂丂丂寢榑
丂丂丂丂丂丂偡側傢偪丄桳堄悈弨5亾偵偍偄偰儕儞僑僟僀僄僢僩慜屻偱桳堄側嵎偑桳傞偙偲偑傢偐傞丅丂丂丂
丂丂丂丂丂丂儕儞僑僟僀僄僢僩偼桳岠偱偁傞偲寢榑晅偗傜傟傞丅
丂丂
丂丂丂仠僂傿儖僐僋僗儞偺晞崋晅弴埵専掕
丂丂丂丂丂僂傿儖僐僋僗儞偺晞崋晅弴埵専掕偼丄2偮偺廤抍娫偱乽懳墳娭學偑桳傞乿応崌偵丄偙偺2偮偺廤抍娫偵桳堄側嵎偑桳傞偐
丂丂丂丂丂偳偆偐傪専掕偡傞応崌偵梡偄傞丅
丂丂丂丂丂椺
丂丂丂丂丂丂嶐擭偲崱擭偺俀夞丄摨堦恖暔偵侾偐寧偺彂愋峸擖戙偵娭偡傞傾儞働乕僩傪幚巤偟偨偲偙傠師昞偺寢壥傪摼偨丅
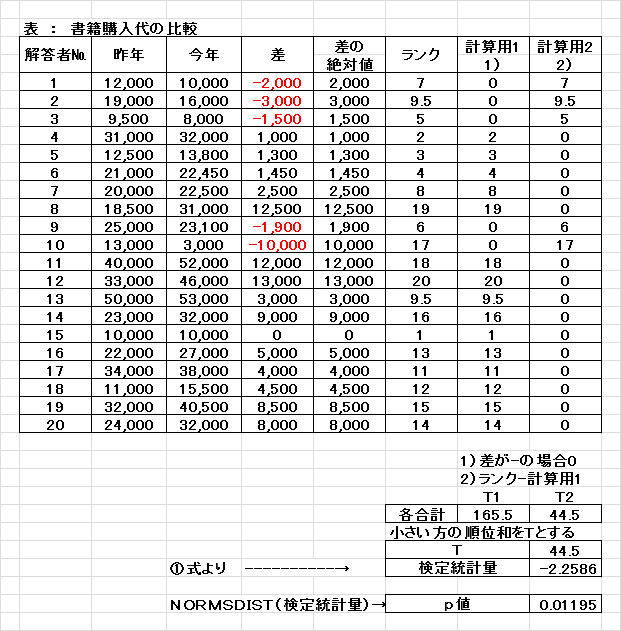 丂丂丂丂丂丂嶐擭偲崱擭偱偼彂愋峸擖戙偵桳堄側嵎偑桳傞偐偳偆偐傪専掕偟側偝偄丅
丂丂丂丂丂丂寢壥
丂丂丂丂丂丂丂倫抣亖0.01195亊2亖0.02391亙桳堄悈弨抣丂0.05
丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮椉懁専掕偱偁傞偺偱2攞乯
丂丂丂丂丂丂寢榑
丂丂丂丂丂丂丂桳堄悈弨5亾偱偼丄婣柍壖愢H0偼婞媝偝傟丄懳棫壖愢H1傪嵦戰偡傞丅
丂丂丂丂丂丂丂廬偭偰丄嶐擭偲崱擭偺彂愋峸擖戙偺娫偵偼桳堄側嵎偑擣傔傜傟傞丅
丂丂丂丂丂倫抣傪媮傔傞寁嶼庤弴
丂丂丂丂丂丂丂嘆2偮偺廤抍偺嵎傪媮傔傞丅
丂丂丂丂丂丂丂嘇嵎偺愨懳抣傪媮傔傞丅
丂丂丂丂丂丂丂嘊嵎偺愨懳抣偵儔儞僋傪晅偗傞丅
丂丂丂丂丂丂丂嘋2偮偺廤抍枅偵儔儞僋抣偺崌寁傪媮傔傞丅
丂丂丂丂丂丂丂嘍崌寁偺彫偝偄曽傪T偲偡傞丅
丂丂丂丂丂丂丂嘐埲壓偺寁嶼幃偱専掕摑寁検Z傪媮傔傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俿亅値亊乮値亅1乯/4
丂丂丂丂丂丂丂丂丂丂丂倅亖-----------------------------------丂丂-------嘆幃
丂丂丂丂丂丂丂丂丂丂丂丂丂丂併乮値亊乮値亅1乯亊乮2値亄1乯/24
丂丂丂丂丂丂丂嘑倫抣傪媮傔傞娭悢丂値倧倰倣倱倓倝倱倲乮倸乯偵傛傝丄倫抣傪媮傔傞丅
丂丂丂丂丂丂丂丂丂丂椉懁専掕偺応崌偼丄偙偺抣傪2攞偟偰桳堄悈弨抣偲斾妑偡傞丅
丂丂丂丂丂丂丂丂丂丂2亊倫抣丂亙丂桳堄悈弨兛偺応崌
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂桳堄悈弨兛偱婣柍壖愢俫0傪婞媝偟偰懳棫壖愢俫1傪嵦戰偡傞丅
丂丂丂丂丂丂丂丂丂丂2亊倫抣丂亜丂桳堄悈弨兛偺応崌
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂桳堄悈弨兛偱婣柍壖愢俫0傪嵦戰偟偰婣柍壖愢俫1傪婞媝偡傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂嶐擭偲崱擭偱偼彂愋峸擖戙偵桳堄側嵎偑桳傞偐偳偆偐傪専掕偟側偝偄丅
丂丂丂丂丂丂寢壥
丂丂丂丂丂丂丂倫抣亖0.01195亊2亖0.02391亙桳堄悈弨抣丂0.05
丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮椉懁専掕偱偁傞偺偱2攞乯
丂丂丂丂丂丂寢榑
丂丂丂丂丂丂丂桳堄悈弨5亾偱偼丄婣柍壖愢H0偼婞媝偝傟丄懳棫壖愢H1傪嵦戰偡傞丅
丂丂丂丂丂丂丂廬偭偰丄嶐擭偲崱擭偺彂愋峸擖戙偺娫偵偼桳堄側嵎偑擣傔傜傟傞丅
丂丂丂丂丂倫抣傪媮傔傞寁嶼庤弴
丂丂丂丂丂丂丂嘆2偮偺廤抍偺嵎傪媮傔傞丅
丂丂丂丂丂丂丂嘇嵎偺愨懳抣傪媮傔傞丅
丂丂丂丂丂丂丂嘊嵎偺愨懳抣偵儔儞僋傪晅偗傞丅
丂丂丂丂丂丂丂嘋2偮偺廤抍枅偵儔儞僋抣偺崌寁傪媮傔傞丅
丂丂丂丂丂丂丂嘍崌寁偺彫偝偄曽傪T偲偡傞丅
丂丂丂丂丂丂丂嘐埲壓偺寁嶼幃偱専掕摑寁検Z傪媮傔傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俿亅値亊乮値亅1乯/4
丂丂丂丂丂丂丂丂丂丂丂倅亖-----------------------------------丂丂-------嘆幃
丂丂丂丂丂丂丂丂丂丂丂丂丂丂併乮値亊乮値亅1乯亊乮2値亄1乯/24
丂丂丂丂丂丂丂嘑倫抣傪媮傔傞娭悢丂値倧倰倣倱倓倝倱倲乮倸乯偵傛傝丄倫抣傪媮傔傞丅
丂丂丂丂丂丂丂丂丂丂椉懁専掕偺応崌偼丄偙偺抣傪2攞偟偰桳堄悈弨抣偲斾妑偡傞丅
丂丂丂丂丂丂丂丂丂丂2亊倫抣丂亙丂桳堄悈弨兛偺応崌
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂桳堄悈弨兛偱婣柍壖愢俫0傪婞媝偟偰懳棫壖愢俫1傪嵦戰偡傞丅
丂丂丂丂丂丂丂丂丂丂2亊倫抣丂亜丂桳堄悈弨兛偺応崌
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂桳堄悈弨兛偱婣柍壖愢俫0傪嵦戰偟偰婣柍壖愢俫1傪婞媝偡傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
亂僩僢僾儁乕僕傊亃
亂慜偺儁乕僕傊亃
丂丂丂丂丂 丂丂丂丂丂寢壥 丂丂丂丂丂丂椉懁専掕偱偁傞偺偱 丂丂丂丂丂丂2亊倫抣亖0.00898亊2亖0.01796亙0.05丂偱偁傞偺偱婣柍壖愢俫0傪婞媝偟偰懳棫壖愢俫1傪嵦戰偡傞丅 丂丂丂丂丂寢榑 丂丂丂丂丂丂偡側傢偪丄桳堄悈弨5亾偵偍偄偰儕儞僑僟僀僄僢僩慜屻偱桳堄側嵎偑桳傞偙偲偑傢偐傞丅丂丂丂 丂丂丂丂丂丂儕儞僑僟僀僄僢僩偼桳岠偱偁傞偲寢榑晅偗傜傟傞丅 丂丂 丂丂丂仠僂傿儖僐僋僗儞偺晞崋晅弴埵専掕 丂丂丂丂丂僂傿儖僐僋僗儞偺晞崋晅弴埵専掕偼丄2偮偺廤抍娫偱乽懳墳娭學偑桳傞乿応崌偵丄偙偺2偮偺廤抍娫偵桳堄側嵎偑桳傞偐 丂丂丂丂丂偳偆偐傪専掕偡傞応崌偵梡偄傞丅 丂丂丂丂丂椺 丂丂丂丂丂丂嶐擭偲崱擭偺俀夞丄摨堦恖暔偵侾偐寧偺彂愋峸擖戙偵娭偡傞傾儞働乕僩傪幚巤偟偨偲偙傠師昞偺寢壥傪摼偨丅
丂丂丂丂丂丂嶐擭偲崱擭偱偼彂愋峸擖戙偵桳堄側嵎偑桳傞偐偳偆偐傪専掕偟側偝偄丅 丂丂丂丂丂丂寢壥 丂丂丂丂丂丂丂倫抣亖0.01195亊2亖0.02391亙桳堄悈弨抣丂0.05 丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮椉懁専掕偱偁傞偺偱2攞乯 丂丂丂丂丂丂寢榑 丂丂丂丂丂丂丂桳堄悈弨5亾偱偼丄婣柍壖愢H0偼婞媝偝傟丄懳棫壖愢H1傪嵦戰偡傞丅 丂丂丂丂丂丂丂廬偭偰丄嶐擭偲崱擭偺彂愋峸擖戙偺娫偵偼桳堄側嵎偑擣傔傜傟傞丅 丂丂丂丂丂倫抣傪媮傔傞寁嶼庤弴 丂丂丂丂丂丂丂嘆2偮偺廤抍偺嵎傪媮傔傞丅 丂丂丂丂丂丂丂嘇嵎偺愨懳抣傪媮傔傞丅 丂丂丂丂丂丂丂嘊嵎偺愨懳抣偵儔儞僋傪晅偗傞丅 丂丂丂丂丂丂丂嘋2偮偺廤抍枅偵儔儞僋抣偺崌寁傪媮傔傞丅 丂丂丂丂丂丂丂嘍崌寁偺彫偝偄曽傪T偲偡傞丅 丂丂丂丂丂丂丂嘐埲壓偺寁嶼幃偱専掕摑寁検Z傪媮傔傞丅 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俿亅値亊乮値亅1乯/4 丂丂丂丂丂丂丂丂丂丂丂倅亖-----------------------------------丂丂-------嘆幃 丂丂丂丂丂丂丂丂丂丂丂丂丂丂併乮値亊乮値亅1乯亊乮2値亄1乯/24 丂丂丂丂丂丂丂嘑倫抣傪媮傔傞娭悢丂値倧倰倣倱倓倝倱倲乮倸乯偵傛傝丄倫抣傪媮傔傞丅 丂丂丂丂丂丂丂丂丂丂椉懁専掕偺応崌偼丄偙偺抣傪2攞偟偰桳堄悈弨抣偲斾妑偡傞丅 丂丂丂丂丂丂丂丂丂丂2亊倫抣丂亙丂桳堄悈弨兛偺応崌 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂桳堄悈弨兛偱婣柍壖愢俫0傪婞媝偟偰懳棫壖愢俫1傪嵦戰偡傞丅 丂丂丂丂丂丂丂丂丂丂2亊倫抣丂亜丂桳堄悈弨兛偺応崌 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂桳堄悈弨兛偱婣柍壖愢俫0傪嵦戰偟偰婣柍壖愢俫1傪婞媝偡傞丅 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂