乻堦尦攝抲偺暘嶶暘愅偵偮偄偰乼
丂丂丂丂仠暘嶶暘愅朄丂丂丂丂
丂丂丂丂丂丂堦尦攝抲偺暘嶶暘愅朄
丂丂丂丂丂丂丂丂暋悢偺妛峑娫偺斾妑傗抧嬫娫側偳丄俁孮丄係孮埲忋偺暯嬒抣偺摨帪斾妑傪偟偨偄応崌偑偁傞丅
丂丂丂丂丂丂丂丂暘嶶暘愅偱偼丄俁孮埲忋偺暯嬒抣偵桳堄側嵎偑桳傞偐偳偆偐傪摨帪斾妑偑偱偒傞僷儔儊僩儕僢僋側庤朄偱偁傞丅
丂丂丂丂丂丂丂丂偦偺応崌丄堦偮偩偗偺梫場傪峫偊丄偦偺忬懺傪偄傠偄傠曄偊偰斾妑偡傞曽朄傪乽堦尦攝抲偺暘嶶暘愅朄乿偲偄偆丅
丂丂丂丂丂昞丗僨乕僞
丂丂丂丂乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗
丂丂丂丂丂丂丂丂丂1丂丂丂丂2丂丂丂丂3丂丂丒丒 j 丒丒丒丂倫丂丂丂丂慡懱
丂丂丂丂---------------------------------------------------------------
丂丂丂丂丂1丂丂丂丂X11丂丂丂X21丂丂丂X31丂丂丂丂丂丂丂丂X倫1
丂丂丂丂丂2丂丂丂丂X12丂丂丂X22丂丂丂X32丂丂丂丂丂丂丂丂X倫2
丂丂丂丂丂3丂丂丂丂X13丂丂丂X23丂丂丂X33丂丂丂丂丂丂丂丂X倫3
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 丂X34
i Xij
丂丂丂-----------------------------------------------------------------
丂丂丂孞傝曉偟悢丂n侾丂丂丂値2丂丂丂値3丂丒丒丒丒丒丒丂丂値倫丂丂丂丂値
丂丂丂-----------------------------------------------------------------
丂丂丂暯嬒抣丂丂丂倣1丂丂丂倣2丂丂丂倣3丂丒丒丒丒丒丒丂丂倣倫丂丂丂丂倣
丂丂丂-----------------------------------------------------------------
丂丂丂丂丂倣1乣倣倫丂丗丂奺僌儖乕僾偺暯嬒抣丂丂丂丂丂丂丂値丂丗丂慡懱偺僨乕僞悢乮屄悢乯
丂丂丂丂丂値1乣値倫丂丗丂奺僌儖乕僾偺僨乕僞悢丂丂丂丂丂丂倣丂丗丂慡懱偺暯嬒抣
丂丂丂丂丂仜暘愅庤弴偼師偺捠傝偱偡丅
丂丂丂丂丂丂丂嘆奺悈弨乮孮丄僌儖乕僾乯偺暯嬒抣傪媮傔傞丅
丂丂丂丂丂丂丂丂丂丂倣1丄倣2丄丒丒丒丒丒丂倣倫
丂丂丂丂丂丂丂嘇慡懱偺暯嬒抣倣傪媮傔傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂倣1亊値1亄倣2亊値2亄丒丒丒丒亄倣倫亊値倫
丂丂丂丂丂丂丂丂丂丂丂倣丂亖丂----------------------------------------------
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂値
丂丂丂丂丂丂丂嘊師幃偵傛傝媺娫曄摦俿1傪媮傔傞
丂丂丂丂丂丂丂丂丂丂丂俿1丂亖丂乮倣1亅倣乯2亊値1亄乮倣2亅倣乯2亊値2亄丒丒丒丒亄乮倣倫亅倣乯2亊値倫
丂丂丂丂丂丂丂嘋師幃傛傝岆嵎曄摦俿俤傪媮傔傞丅
丂丂丂丂丂丂丂丂丂丂丂岆嵎曄摦俿俤丂亖丂乮奺悈弨偺應掕抣亅奺悈弨偺暯嬒抣乯2偺憤榓
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖乮倃11亅倣1乯2亄乮倃12亅倣1乯2亄丒丒丒丒亄乮倃21亅倣2乯2亄乮倃22亅倣2乯2亄丒丒丒
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丒丒亄乮倃31亅倣3乯2亄丒丒丒
丂丂丂丂丂丂丂丂丂丂丂岆嵎曄摦俿俤丂亖丂慡曄摦俿亅俿1丂仼----丂慡曄摦俿亖媺娫曄摦俿1亄岆嵎曄摦俿俤
丂丂丂丂丂丂丂丂側偍丄慡曄摦俿偼
丂丂丂丂丂丂丂丂丂丂丂慡曄摦俿丂亖丂乮倃11亅倣乯2亄乮倃12亅倣乯2亄丒丒丒丒亄乮倃ij亅m乯2亄丒丒丒丒亄乮倃倫1亅倣乯2亄丒丒丒
丂丂丂丂丂丂丂嘍媺娫曄摦偍傛傃岆嵎曄摦偺晄曃暘嶶倁1丄倁俤傪師幃傛傝媮傔傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俿1
丂丂丂丂丂丂丂丂丂丂丂倁1丂亖丂----------------
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮倫亅1乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俿俤丂
丂丂丂丂丂丂丂丂丂丂丂倁俤丂亖丂---------------
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮値亅倫乯
丂丂丂丂丂丂丂嘐専掕摑寁検俥1傪師幃傛傝媮傔傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂倁1
丂丂丂丂丂丂丂丂丂丂丂俥1丂亖丂----------------
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂倁俤
丂丂丂丂丂丂丂嘑俥暘晍昞偐傜丄桳堄悈弨兛丄帺桼搙倓倖乮倫亅1丄値亅倫乯偺俥抣傪撉庢傝丄嘐偱媮傔偨専掕摑寁検俥1偲斾妑偡傞丅
丂丂丂丂丂丂丂丂丂丂丂丂俥1亞俥乮兛丄倫亅1丄値亅倫乯偺応崌
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂桳堄悈弨兛偱桳堄嵎偁傝乮懳棫壖愢傪嵦戰偡傞乯
丂丂丂丂丂丂丂丂丂丂丂丂俥1亙俥乮兛丄倫亅丄値亅倫乯偺応崌
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂桳堄悈弨兛偱桳堄嵎側偟乮婣柍壖愢傪嵦戰偡傞乯
丂丂丂丂丂丂丂丂昞丗暘嶶暘愅昞
丂丂丂丂丂丂丂丂------------------------------------------------------------------
丂丂丂丂丂丂丂丂丂曄摦梫場丂丂丂曄摦丂丂丂丂帺桼搙丂丂晄曃暘嶶丂丂丂暘嶶斾丂丂丂丂俥嫬奅抣
丂丂丂丂丂丂丂丂-------------------------------------------------------------------------丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂僌儖乕僾娫丂丂媺娫曄摦俿1丂丂倫亅侾丂丂丂倁1丂丂丂丂 倁1/倁俤
丂丂丂丂丂丂丂丂僌儖乕僾撪丂丂岆嵎曄摦俿俤丂 値亅倫丂丂丂倁俤丂丂丂乮専掕摑寁検乯
丂丂丂丂丂丂丂丂-------------------------------------------------------------------------
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂慡曄摦丂俿丂丂丂値亅1
丂丂丂丂丂丂丂丂-------------------------------------------------------------------------
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂慡曄摦俿丂亖丂媺娫曄摦俿侾丂亄丂岆嵎曄摦俿俤
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂岆嵎曄摦俿俤丂亖丂慡曄摦俿丂亅丂媺娫曄摦俿侾
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂慡曄摦俿丂亖丂儼乮奺悈弨偺應掕抣倃倝倞丂亅丂慡暯嬒抣倣乯俀
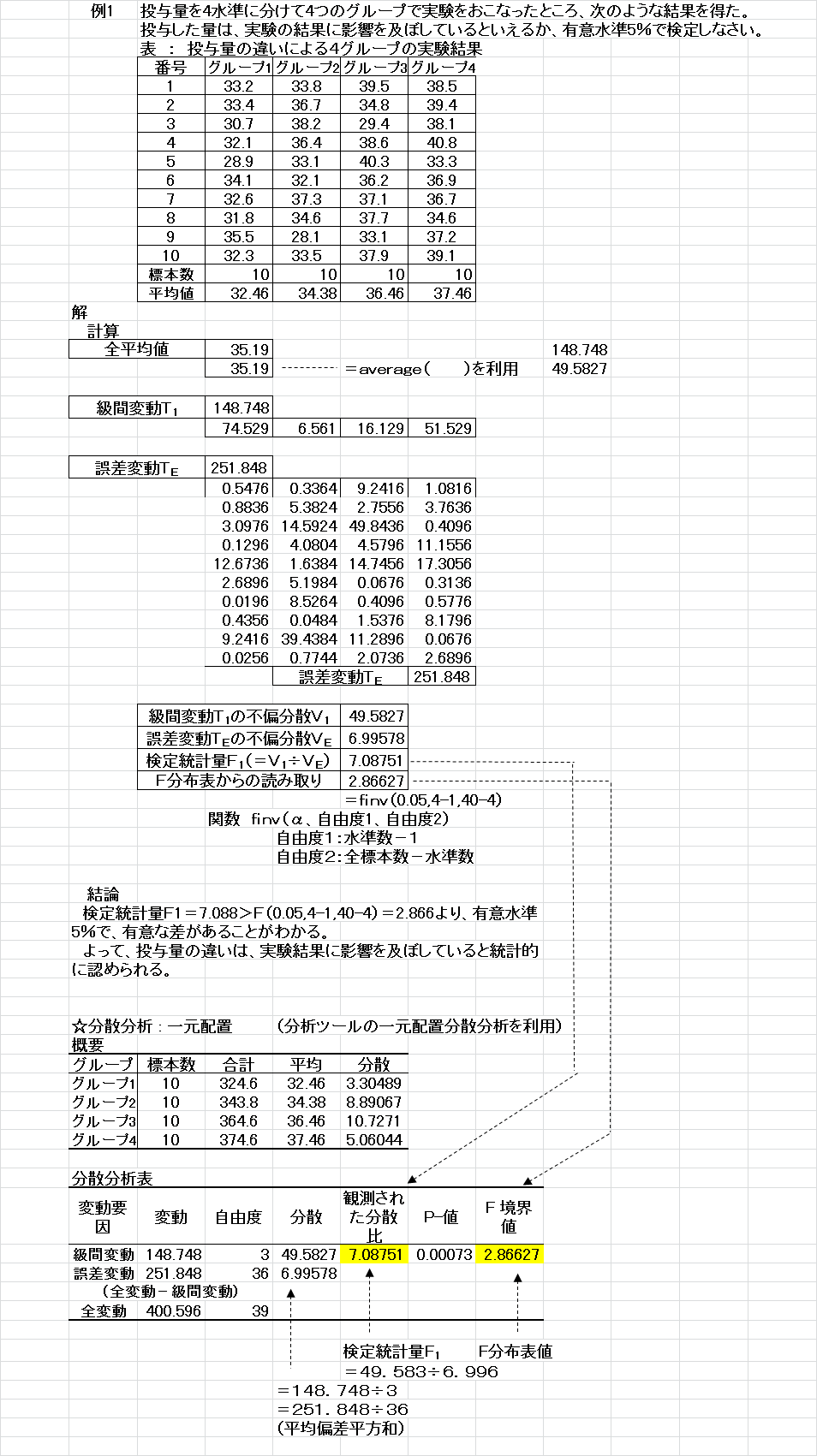
椺侾丂搳梌検傪係悈弨偵暘偗偰係偮僌儖乕僾偱幚尡傪峴偭偨偲偙傠丄師偺條側寢壥傪摼偨丅
丂丂丂搳梌偟偨検偼丄幚尡偵塭嬁傪媦傏偟偰偄傞偲塢偊傞偐偳偆偐丄桳堄悈弨俆亾偱専掕偟側偝偄丅
丂丂丂丂丂丂丂丂昞丗搳梌検偺堘偄偵傛傞係僌儖乕僾偺幚尡寢壥
丂丂丂丂丂丂丂---------------------------------------------------------------
丂丂丂丂丂丂丂丂噦丂丂丂僌儖乕僾侾丂丂僌儖乕僾2丂丂僌儖乕僾3丂丂僌儖乕僾4
丂丂丂丂丂丂丂---------------------------------------------------------------丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂1丂丂丂丂33.2丂丂丂丂丂33.8丂丂丂丂丂39.5丂丂丂丂38.5
丂丂丂丂丂丂丂丂2丂丂丂丂33.4丂丂丂丂丂36.7丂丂丂丂丂34.8丂丂丂丂39.4
丂丂丂丂丂丂丂丂3丂丂丂丂30.7丂丂丂丂丂38.2丂丂丂丂丂29.4丂丂丂丂38.1
丂丂丂丂丂丂丂丂4丂丂丂丂32.7丂丂丂丂丂36.4丂丂丂丂丂38.6丂丂丂丂40.8
丂丂丂丂丂丂丂丂5丂丂丂丂28.9丂丂丂丂丂33.1丂丂丂丂丂40.3丂丂丂丂33.3
丂丂丂丂丂丂丂丂6丂丂丂丂28.9丂丂丂丂丂33.1丂丂丂丂丂40.3丂丂丂丂33.3
丂丂丂丂丂丂丂丂7丂丂丂丂32.6丂丂丂丂丂37.3丂丂丂丂丂37.1丂丂丂丂36.7
丂丂丂丂丂丂丂丂8丂丂丂丂31.8丂丂丂丂丂34.6丂丂丂丂丂37.7丂丂丂丂34.6
丂丂丂丂丂丂丂丂9丂丂丂丂35.5丂丂丂丂丂28.7丂丂丂丂丂33.1丂丂丂丂37.2
丂丂 丂丂丂丂丂10丂丂丂丂32.3丂丂丂丂丂33.5丂丂丂丂丂37.9丂丂丂丂39.1
丂丂丂丂丂丂丂--------------------------------------------------------------
丂丂丂丂丂丂丂昗杮悢丂丂丂10丂丂丂丂丂丂10丂丂丂丂丂丂10丂丂丂丂 10
丂丂丂丂丂丂丂暯嬒抣丂丂 32.46丂丂丂丂丂34.38丂丂 丂丂36.346丂 丂37.46
丂丂丂丂丂丂丂--------------------------------------------------------------
丂
丂丂丂丂夝
丂丂丂丂丂寁嶼
丂丂丂丂丂丂丂丂丂慡暯嬒抣丂亖丂35.19
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂35.19丂丂仼-----丂亖倎倴倕倰倎倗倕乮僨乕僞斖埻乯傪棙梡
丂丂丂丂丂丂丂丂丂媺娫曄摦俿1丂亖丂148.748丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂------------------------------------------------
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 74.529丂丂丂丂丂6.561丂丂丂16.129丂丂丂51.529
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂-------------------------------------------------
丂丂丂丂丂丂丂丂丂岆嵎曄摦俿俤丂亖丂251.848
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂-------------------------------------------------
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂0.5476丂丂丂0.3364丂丂丂丂9.2416丂丂1.0816
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂0.8836丂丂丂5.3824丂丂丂丂2.7556丂丂3.7636
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂3.0976丂 丂14.5924丂 丂丂49.8436丂丂0.4096
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂0.1296丂丂丂4.0804丂丂丂丂4.5796丂 11.1556
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 12.6736丂丂丂1.6984丂 丂丂14.7456 丂17.3056
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂2.6896丂丂丂5.1984丂丂丂丂0.0676丂丂0.3136
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂0.0196丂丂丂0.85264丂丂丂0.4096丂 丂0.5776
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂0.4356丂丂丂0.0484丂丂 丂1.5376丂 丂8.1796
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂9.2416丂丂丂39.4384丂丂丂11.2896丂丂0.0676
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂0.0256丂丂丂0.7744丂丂丂丂2.0736丂丂2.6896
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂--------------------------------------------------
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂岆嵎曄摦俿俤 251.848
------------------------
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂媺娫曄摦俿侾偺晄曃暘嶶倁侾丂亖丂16560.73
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂岆嵎曄摦俿俤偺晄曃暘嶶倁俤丂亖丂6.995778
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂専掕摑寁検俥侾乮亖倁侾亐倁俤乯亖 7.08751丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俥暘晍昞偐傜偺撉庢傝丂丂丂丂亖丂2.866266
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂娭悢丂亖倖倝値倴乮兛丄帺桼搙1丄帺桼搙2乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂帺桼搙1丗悈弨悢亅侾
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂帺桼搙2丗慡昗杮悢亅悈弨悢
丂丂丂丂丂寢榑
丂丂丂丂丂丂丂専掕摑寁検俥侾亖7.088亜2.866亖俥乮0.05丄4亅1丄40亅4乯傛傝丄桳堄悈弨俆亾偱桳堄側嵎偑偁傞偙偲偑傢偐傞丅
丂丂丂丂丂丂丂廬偭偰丄搳梌検偺堘偄偼丄幚尡寢壥偵塭嬁傪媦傏偟偰偄傞偲摑寁揑偵擣傔傜傟傞丅
丂丂丂丂仚暘嶶暘愅丗堦尦攝抲丂丂乮暘愅僣乕儖偺堦尦攝抲偺暘嶶暘愅傪棙梡乯
丂丂丂丂丂丂丂奣梫
丂丂丂丂丂丂丂亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖
丂丂丂丂丂丂丂丂僌儖乕僾丂丂丂丂昗杮悢丂丂丂崌寁丂丂丂暯嬒丂丂丂暘嶶
丂丂丂丂丂丂丂----------------------------------------------------------------
丂丂丂丂丂丂丂丂僌儖乕僾1丂丂丂丂10丂丂丂丂丂324.6丂丂丂32.46丂丂3.30489
丂丂丂丂丂丂丂丂僌儖乕僾2丂丂丂丂10丂丂丂丂丂343.8丂丂丂34.38丂丂8.89067
丂丂丂丂丂丂丂丂僌儖乕僾3丂丂丂丂10丂丂丂丂丂364.6丂丂丂36.46丂 10.7271
丂丂丂丂丂丂丂丂僌儖乕僾4丂丂丂丂10丂丂丂丂丂374.6丂丂丂37.46丂丂5.0644
丂丂丂丂丂丂丂亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖
丂丂丂丂丂丂丂暘嶶暘愅昞
丂丂丂丂丂丂丂亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖
丂丂丂丂丂丂丂曄摦梫場丂丂曄摦丂丂丂帺桼搙丂丂暘嶶丂丂丂娤嶡偝傟偨暘嶶斾丂丂俹乚抣丂丂丂俥嫬奅抣
丂丂丂丂丂丂丂--------------------------------------------------------------------------------
丂丂丂丂丂丂丂媺娫曄摦丂丂148.748丂丂丂3丂丂丂49.5827丂丂丂7.08751丂丂丂丂丂0.00073丂丂丂2.86627
丂丂丂丂丂丂丂岆嵎曄摦丂丂251.848丂丂丂36丂丂丂6.99578
丂丂丂丂丂丂乮慡曄摦亅媺娫曄摦乯
丂丂丂丂丂丂丂慡曄摦 400.596 39丂丂丂丂丂丂
丂丂丂丂丂丂丂亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂仾丂丂丂丂丂丂仾丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂仾
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丗丂丂丂丂丂専掕摑寁検俥1丂丂丂丂丂丂丂丂俥暘晍昞抣丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丗丂丂丂丂丂丂亖49.583亐6.996丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖148.748亐3
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖251.848亐36
徻嵶偼壓恾傪嶲徠
亂僩僢僾儁乕僕傊亃
亂慜偺儁乕僕傊亃