乻婎丂杮丂摑丂寁丂妛丂18乼
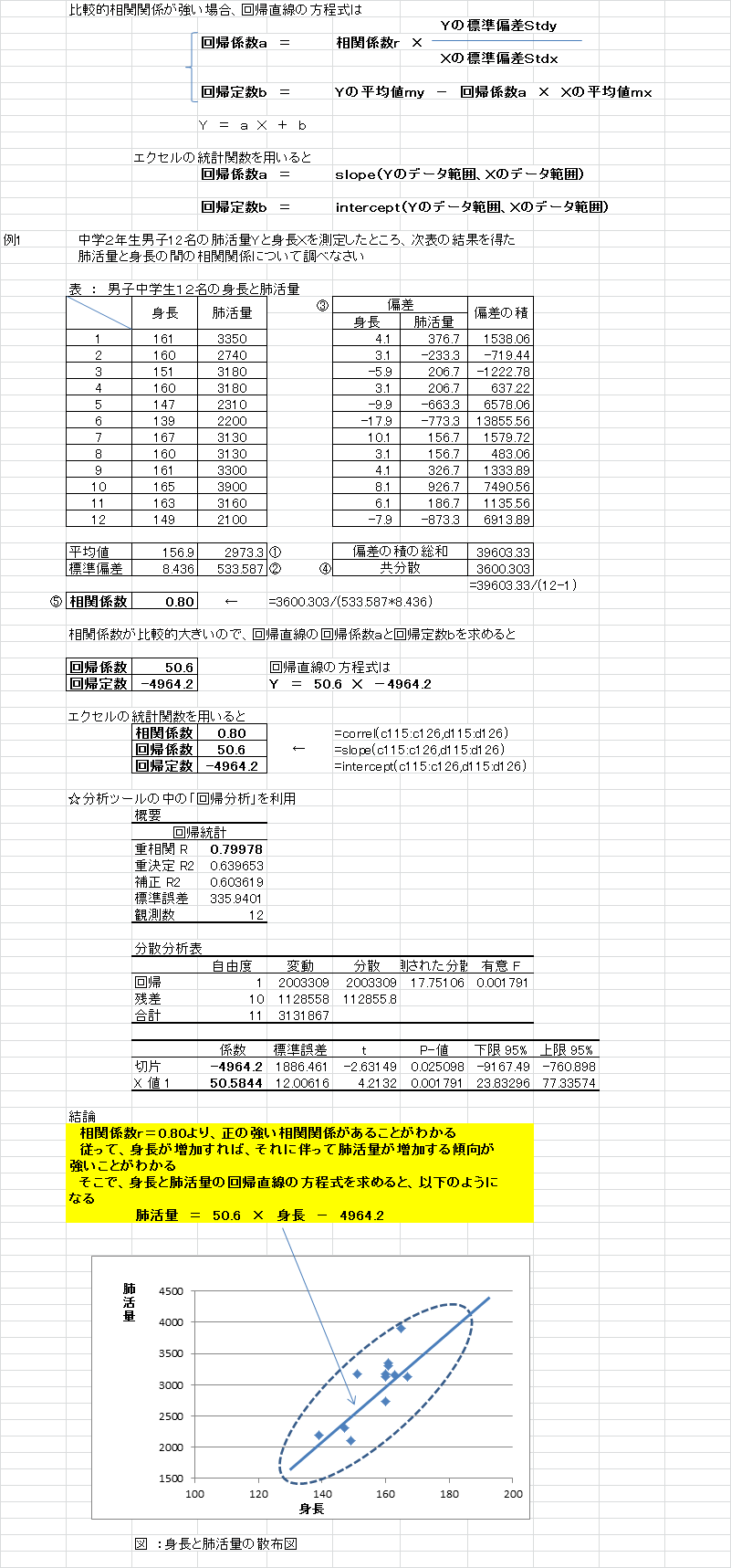
丂丂丂丂椺丂拞妛俀擭惗抝巕侾俀柤偺攛妶検偲恎挿傪應掕偟偨偲偙傠丄師偺昞偺條側寢壥傪摼偨丅
丂丂丂丂丂丂攛妶検偲恎挿偲偺娫偺憡娭娭學偵偮偄偰挷傋側偝偄丅
丂丂丂丂丂丂昞丂丗丂抝巕拞妛俀擭惗侾俀柤偺恎挿偲
丂丂丂丂丂丂丂丂丂丂攛妶検
丂丂丂丂丂丂------------------------------------丂--------------------------------丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂曃嵎丂丂丂丂丂 丂丂
丂丂丂丂丂丂丂丂丂丂恎挿丂丂丂丂丂丂丂攛妶検丂 丂-------------------丂丂曃嵎偺愊
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂恎挿丂丂丂攛妶検
---------------------------------- --------------------------------
丂丂丂丂丂丂丂1丂 丂161丂 丂丂丂丂丂丂3350丂丂丂丂4.1丂丂丂 丂376.7丂丂丂1538.056
丂丂丂丂丂丂丂2丂丂 160丂丂 丂丂丂丂丂2740丂丂丂丂3.1丂丂丂丂-2333.3丂丂丂-719.444
丂丂丂丂丂丂丂3丂 丂151丂丂丂 丂丂丂丂3180丂丂 丂-5.9 丂丂丂丂206.7丂 丂-1222.78
丂丂丂丂丂丂丂4 160 3180 3.1 206.7 637.2222
丂丂丂丂丂丂丂5 147 2310 -9.9 -663.3 6578.056
丂丂丂丂丂丂丂6 139 2200 -17.9 -773.3 13855.56
丂丂丂丂丂丂丂7 167 3130 10.1 156.7 1579.722丂
丂丂丂丂丂丂丂8 160 3130 3.1 156.7 483.0556
丂丂丂丂丂丂丂9 161 3300 4.1 326.7 1333.889
丂丂丂丂丂 丂10 165 3900 8.1 926.7 7490.556
丂丂丂丂丂丂 11 163 3160 6.1 186.7 1135.556
丂丂丂丂丂丂 12 149 2100 -7.9 -873.3 6913.889
丂丂丂丂丂------------------------------------ -----------------------------------
丂丂丂丂丂暯嬒抣 156.9 2973.3 曃嵎偺愊偺憤榓丂丂丂 丂39603.33
丂丂丂丂丂昗弨曃嵎 8.436 533.587 -----------------------------------
------------------------------------
丂丂丂丂丂夝
丂丂丂丂丂丂丂丂憡娭學悢倰丂亖丂0.800丂仼--------丂亖嫟暘嶶/俀偮偺昗弨曃嵎偺愊
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖們倧倰倰倕倢乮倄偺僨乕僞斖埻丄倃偺僨乕僞斖埻乯
丂丂丂丂丂寢榑
丂丂丂丂丂丂丂丂憡娭學悢倰亖0.800傛傝丄惓偺嫮偄憡娭娭學偑偁傞偙偲偑暘偐傞丅
丂丂丂丂丂丂丂丂廬偭偰丄恎挿偑憹壛偡傟偽丄偦傟偵敽偭偰攛妶検偑憹壛偡傞孹岦偑嫮偄偙偲偑暘偐傞丅
丂丂丂丂丂丂丂丂憡娭學悢偑斾妑揑戝偒偄偺偱丄夞婣捈慄偺曽掱幃傪媮傔傞偲
丂丂丂丂丂丂丂丂丂丂丂夞婣學悢倎亖50.6丂丂仼------丂憡娭學悢倰 亊 倄偺昗弨曃嵎 / 倃偺昗弨曃嵎亖0.800亊533.587/8.436
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂摑寁娭悢 亖倱倢倧倫倕乮倄偺僨乕僞斖埻丄倃偺僨乕僞斖埻乯
丂丂丂丂丂丂丂丂丂丂丂夞婣掕悢倐亖-4964.2丂仼-----丂倄偺暯嬒抣 亅 夞婣學悢倎 亊 倃偺暯嬒抣倣倶亖2973.3亅50.6亊156.9
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂摑寁娭悢 亖倝値倲倕倰們倕倫倲乮倄偺僨乕僞斖埻丄倃偺僨乕僞斖埻乯
丂丂丂丂丂丂丂丂丂丂丂夞婣捈慄偺曽掱幃丂丂倄 亖 50. 6 倃 亅 4964.2
丂丂丂丂仢憡娭學悢偺桳堄惈偺専掕
丂丂丂丂丂丂丂憡娭娭學偑傎偲傫偳側偄偲巚傢傟傞応崌偱傕丄僨乕僞偺拪弌曽朄偑揔摉偱側偐偭偨傝偟偰桳堄偵側傞応崌偑偁傞丅
丂丂丂丂丂丂丂偙偺條側応崌偼丄憡娭學悢偺桳堄惈偺専掕傪峴偆丅
丂丂丂丂丂丂丂偄傑丄偁傞昗杮廤抍偺倰倱偑梌偊傜傟偰偄傞偲偒丄桳堄悈弨兛偱憡娭學悢偑桳堄偐偳偆偐偺敾掕傪偡傞丅丂丂丂丂丂丂
丂丂丂丂丂丂丂偦偺庤弴偼師偺捠傝偱偡丅
丂丂丂丂丂丂丂丂丂嘆曣廤抍偺憡娭學悢倰倱偑侽偱偁傞偲偟偰丄昗杮偺憡娭學悢偲曣廤抍偺憡娭學悢偲偺娫偵偼嵎偑柍偄偲壖掕偡傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂乮婣柍壖愢偵憡摉偡傞乯
丂丂丂丂丂丂丂丂丂嘇師幃偵傛偭偰丄専掕摑寁検倲傪媮傔傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂倰倱丂亊丂併乮値亅2乯
丂丂丂丂丂丂丂丂丂丂丂丂専掕摑寁検倲丂亖丂---------------------------
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂併乮1亅倰倱2乯
丂丂丂丂丂丂丂丂丂嘊倲暘晍昞偐傜丄帺桼搙倓倖亖値亅2丄桳堄悈弨兛偺倲暘晍昞抣傪撉傒庢傞
丂丂丂丂丂丂丂丂丂丂丂丂亖倲倝値倴乮兛丄値亅2乯
丂丂丂丂丂丂丂丂丂嘋専掕摑寁検倲偲倲暘晍昞抣偲偺抣傪斾妑偡傞丅
丂丂丂丂丂丂丂丂丂丂丂丂専掕摑寁検倲亞倲乮兛丄値亅2乯偺応崌
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂懳棫壖愢傪嵦戰偟偰婣柍壖愢傪婞媝偡傞
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂桳堄悈弨兛偱桳堄惈偁傝
丂丂丂丂丂丂丂丂丂丂丂丂専掕摑寁検倲亙倲乮兛丄値亅2乯偺応崌
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂懳棫壖愢傪婞媝偟偰婣柍壖愢傪嵦戰偡傞
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂桳堄悈弨兛偱桳堄惈側偟丂丂丂丂丂
徻嵶偼壓恾傪嶲徠丂丂丂丂丂丂
丂丂
亂僩僢僾儁乕僕傊亃
亂慜偺儁乕僕傊亃

