《基　本　統　計　学　16》 



　　　　　　◎差を調べる方法
　　　　　　　　次の様な計算を各値に対して行い、その総合計を求める。
　　　　　　　　　　　　　　（Ｏ―Ｅ）２
　　　　　　　　　　Σ（　---------------） ・・・・・・・・・・・　検定統計量χ２値
　　　　　　　　　　　　　　　　Ｅ　　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　この総合計の事を検定統計量χ２値という。　　　　　　　　　  
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
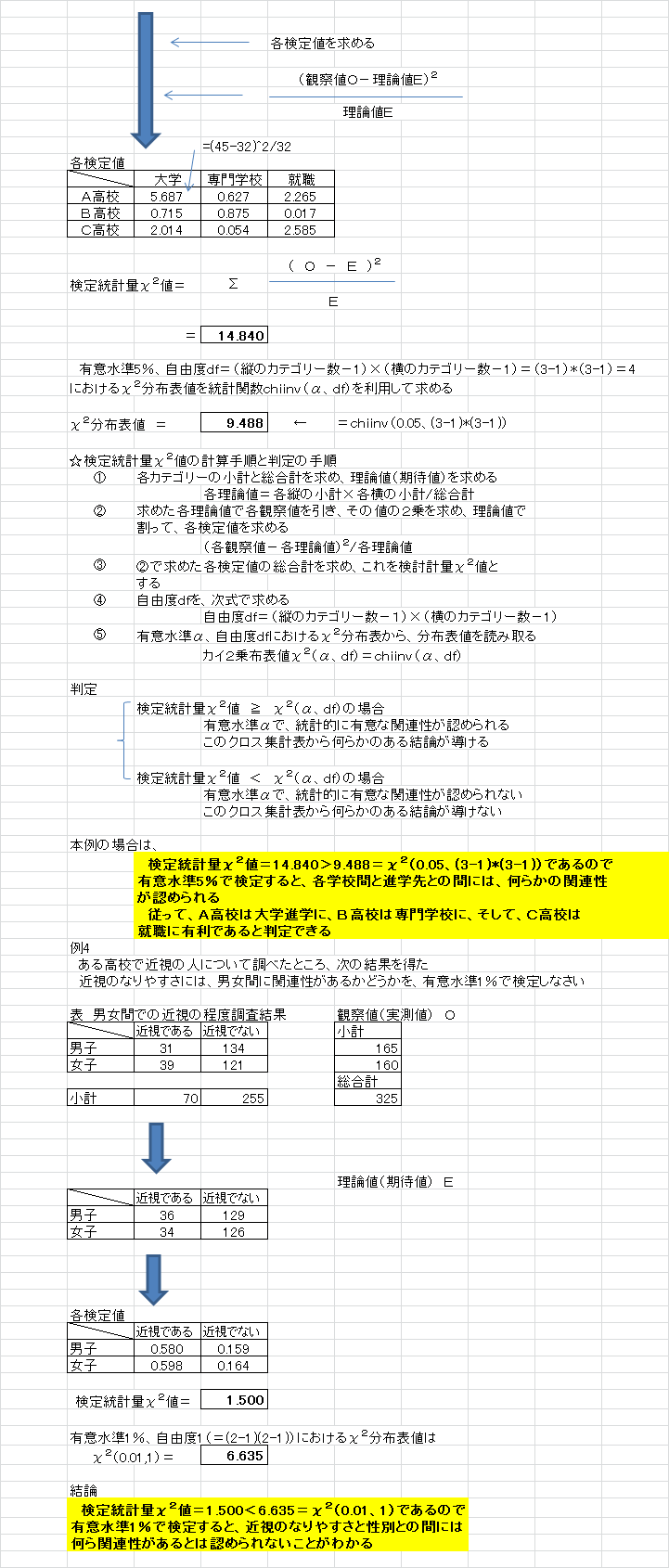
　　　　　　　　　表：各検定値　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　---------------------------------------------------------　　　　　　
　　　　　　　　　　　　　大学進学ａ　　　専門学校進学ｂ　　　就職ｃ　　　　　　　　　
　　　　　　　　---------------------------------------------------------　　　　　　
　　　　　　　　　Ａ高校　　　5.687　　　　　　0.627　　　　　   2.265　　　　　　 
　　　　　　　　　Ｂ高校　　　0.715　　　　 　 0.875　　　　　   0.017　　　　　　　　　　
　　　　　　　　　Ｃ高校      2.014           0.054             2.585　　　　　　　
　　　　　　　　---------------------------------------------------------　　　　　　
　　　　　　　　　　　　　　　　　　　　　　：　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　：　←----　総合計　
　　　　　　　　　　　　　　　　　　　　　　：
　　　　　　　　　　　　　　　　　　　　　　↓
　　　　　　　　　　　　　検定統計量χ２値＝14.840

　　　　　　　　計算によって求めた検定統計量χ２値とχ２分布表から読み取ったχ２値（α、ｄｆ）との値を比較する。

　　　　　　☆検定統計量χ２値の計算方法と判定手順
　　　　　　　　�@ 各カテゴリーの小計を求め、理論値（期待値）を計算する。
　　　　　　　　　　　　　各期待値＝各横のカテゴリーの小計×各縦のカテゴリーの小計/総合計

　　　　　　　　�A 求めた理論値で観察値を引き、その２乗を求め理論値で割り、各検定量を求める
　　　　　　　　�B �Aで求めた各検定量の総合計を求める。この値を検定統計量χ２値と云う。
　　　　　　　　�C 自由度ｄｆ＝（横のカテゴリー数−1）×（縦のカテゴリー数−1）を求める
　　　　　　　　�D 有意水準αを定め、χ２分布表から得られた値と比較する。

　　　　　　　判定
　　　　　　　　　検定統計量χ２値　≧　χ２分布表値（α、ｄｆ）の場合
　　　　　　　　　　　　　　有意水準αで有意差があると判定
　　　　　　　　　　　　　　集計表から読取り、ある結論を導ける
　　　　　　　　　検定統計量χ２値　≦　χ２分布表値（α、ｄｆ）の場合
　　　　　　　　　　　　　　有意水準αで有意差なしと判定
　　　　　　　　　　　　　　この表からは結論は導けない

　　　　　　　この例の場合は
　　　　　　　　　χ２分布表値（0.05、4）＝9.488　←-------　ｃｈｉｉｎｖ（0.05、（3-1）×（3-1））
　　　　　　　　　検定統計量χ２値　＝　14.840

　　　　　　結論
　　　　　　　　検定統計量χ２値＝14.840＞9.488＝χ２分布表値（0.05、4）であるので、有意水準５％で有意の差がある事が分かる。
　　　　　　　　すなわち、各高校間で、大学進学、専門学校と就職について差（関連性）がある事が分かる。

　　　　　　なお、ｐ値を求めるエクセル関数の書式は、以下の通りです。
　　　　　　　　＝ｃｈｉｄｉｓｔ（検定統計量χ２値、自由度）

　　　　　　　　本例の場合は、
　　　　　　　　　　ｐ値＝0.005045　　←------　＝chidist（14.840、(3-1)*(3-1))
                   すなわち、ｐ＞0.005となる　　　　　　　　　　　　　　　　　　　　　　　　

　　　　　　
　　　　　　例４　ある高校で金氏の人について調べたところ、次の結果を得た。
　　　　　　　　　近視の成り易さには、男女間に関連性があるかどうかを有意水準１％で検定しなさい。

　　　　　　　　　　　　　　　表　：　男女間での近視の程度の調査結果
　　　　　　　　　　　　　　------------------------------------------------
　　　　　　　　　　　　　　　　　　　近視である　　　近視でない　　　小計
　　　　　　　　　　　　　　------------------------------------------------
　　　　　　　　　　　　　　　男子　　　31　　　　　　　134　　　　　　165
　　　　　　　　　　　　　　　女子　　　39　　　　　　　121　　　　　　160
　　　　　　　　　　　　　　------------------------------------------------
　　　　　　　　　　　　　　　小計　　　70　　　　　　　255　　　　　　325
　　　　　　　　　　　　　　------------------------------------------------
　　　　　　　　　　　　　　　　　　　　　　　　　　：
　　　　　　　　　　　　　　　　　　　　　　　　　　：
　　　　　　　　　　　　　　　理論値（期待値）　　　↓
　　　　　　　　　　　　　　------------------------------------------------
　　　　　　　　　　　　　　　　　　　　　近視である　　　近視でない　　　
　　　　　　　　　　　　　　------------------------------------------------
　　　　　　　　　　　　　　　男子　　　　　　36　　　　　　129
　　　　　　　　　　　　　　　女子　　　　　　34　　　　　　126
　　　　　　　　　　　　　　------------------------------------------------
　　　　　　　　　　　　　　　　　　　　　　　　　　：
　　　　　　　　　　　　　　　　　　　　　　　　　　：
　　　　　　　　　　　　　　　各検定値　　　　　　　↓
　　　　　　　　　　　　　　------------------------------------------------
　　　　　　　　　　　　　　　　　　　　　近視である　　　近視でない　　　
　　　　　　　　　　　　　　------------------------------------------------
　　　　　　　　　　　　　　　男子　　　　　0.580　　　　　　0.159
　　　　　　　　　　　　　　　女子　　　　　0.598　　　　　　0.164
　　　　　　　　　　　　　　------------------------------------------------

　　　　　　　　　　　　　　　検定統計量χ２値＝1.500

　　　　　　　　　　　　　　　有意水準１％、自由度ｄｆ＝１（＝(2-1)(2-1)）のχ２分布表値は
　　　　　　　　　　　　　　　　　χ２（0.01、(2-1)(2-1)）＝6.635　　←-----　chiinv（0.01、(2-1)(2-1)）

　　　　　　　　結論
　　　　　　　　　　検定統計量χ２値＝1.500＜6.635＝χ２（0.01、(2-1)(2-1)）であるので、
　　　　　　　　　男女間の性別で近視の成り易さには、何らに関連性があるとは認められないと判定できる。
　　　　　　　　　　

詳細は下図を参照