《基　本　統　計　学　11》

　　　　●統計分析（基本）
　　　　　　　
　　　　　　　・推定処理
　　　　　　　・検定処理
　　　　　　　・相関と回帰
　　　　　　　　　（１変量、もしくは２変量間の関係について）

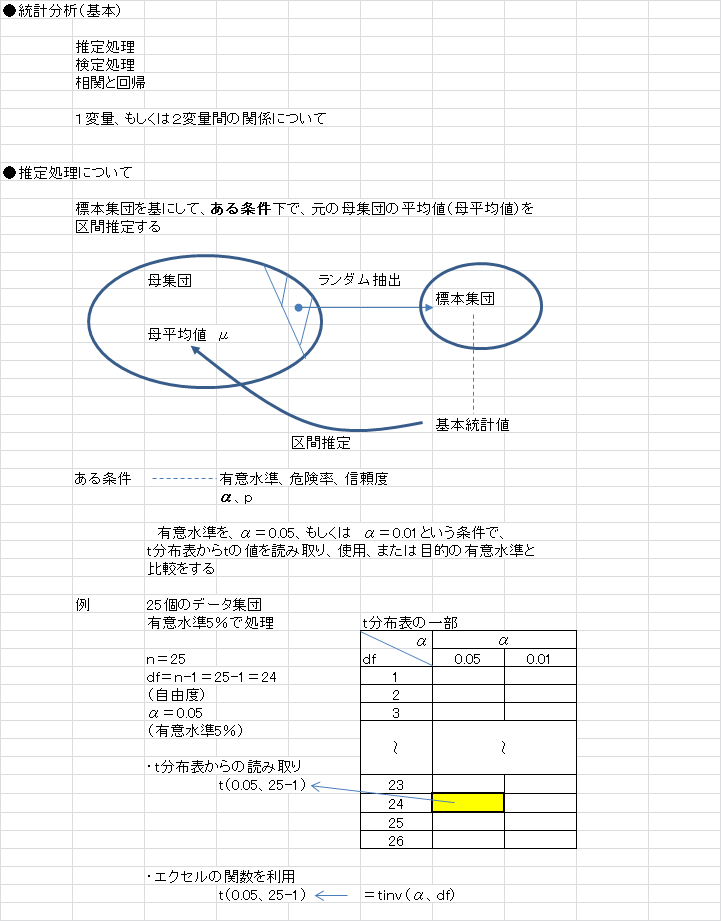
　　　　●推定処理
　　　　　　標本勇断を基にして、ある条件下で元のの母集団の値（平均値）を推定する。

　　　　　　母平均値の区間推定
　　　　　　　　　ある条件　・・・・　信頼度、有意水準、危険率
　　　　　　　　　　　　　　　　　　　　α、ｐで代表する
　　　　　　　　　　　　　有意水準α＝0.05、or　α＝0.01で、ｔ分布表から読取り、使用、または目的の有意水準と
　　　　　　　　　　　　　比較する。

　　　　　　　例　　25個のデータ集団　　　　　　　　　　　ｔ分布表
　　　　　　　　　　有意水準5％（α＝0.05）　　　　　　--------------------------------
　　　　　　　　　　で処理の場合　　　　　　　　　　　　　　　　　　　　　α
　　　　　　　　　　　　　　　　　　　　　　　　　　　　ｄｆ　　------------------------　
　　　　　　　　　　ｎ＝25　　　　　　　　　　　　　　　　　　　　0.05　　　　　0.01
　　　　　　　　　ｄｆ＝25-1　　　　　　　　　　　　　---------------------------------　
　　　　　　　　　　（自由度、標本数-１　　　　　　　　　1　　 　　↓
　　　　　　　　　　α＝0.05　　　　　　　　　　　　　---------------------------------
　　　　　　　　　　　　　　　　　　　　　　　　　　　　 2 　　　　↓
　　　　　　　　　　・ｔ分布表からの読取り　　　　　　----------------------------------
　　　　　　　　　　　　　ｔ（0.05、25-1）→　◎値　　　 3  　　 　↓  
　　　　　　　　　　・エクセルの関数を利用　　　　　　----------------------------------　　　
                         ＝ｔｉｎｖ（α、ｄｆ）　　　　・         ↓      
　　　　　　　　　　　　　　　　　　　　　　　　　　　-----------------------------------
　　　　　　　　　　　　　　　　　　　　　　　　　　　　・         ↓
　　　　　　　　　　　　　　　　　　　　　　　　　　　-----------------------------------
　　　　　　　　　　　　　　　　　　　　　　　　　　　　24　→ →　◎　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　-----------------------------------
　　　　　　　　　　　　　　　　　　　　　　　　　　　　25
　　　　　　　　　　　　　　　　　　　　　　　　　　　-----------------------------------
　　　　　　　　　　　　　　　　　　　　　　　　　　　　26
　　　　　　　　　　　　　　　　　　　　　　　　　　　------------------------------------
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　この値◎をｔ分布表から読み取る
　　　　　　　　ｔ分布表からの読取り
　　　　　　　　　　ｔ(0.05,25-1）＝◎値
　　　　　　　　　　　　　　　　　　　　ランダム抽出
　　　　　　　　　　　　母集団　-------------------------→　標本集団
　　　　　　　　　　　　　母平均値μ＝？　　　　　　　　　　　　データ　　　　：　ｘ1、ｘ2、・・・・、ｘｎ
　　　　　　　　　　　　　母標準偏差＝？　　←-------------　　標本数　　　　：　ｎ
　　　　　　　　　　　　　　　　　　　　　区間推定する　　　　　標本平均値　　：　ｍ
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　標本標準偏差　：　Ｓｔｄ　　　　　
　　　　　　　　ある統計的条件で推定する
　　　　　　　　　　その場合、使用する語句は以下の用語を使用する
　　　　　　　　　　　　有意水準、危険率、信頼度（水準）、α、ｐ
　　　　　　　　　　また、統計学の慣例として、次の２条件で処理する場合が多い。
　　　　　　　　　　　　α＝0.01、0.05

　　　　　　　　α＝0.01の場合　・・・・　有意水準1％、危険率1％、信頼度99％、α
　　　　　　　　　　　　　　　　　　　　　１００個のデータのうち９９個まではその様に云えるが、あとの１個についてはその
　　　　　　　　　　　　　　　　　　　　　様に云えるかどうかわからない。　
　　　　　　　　α＝0.05の場合　・・・・　有意水準5％、危険率5％、信頼度95％、α
　　　　　　　　　　　　　　　　　　　　　１００個のデータのうち９５個まではその様に云えるが、あとの５個についてはその
　　　　　　　　　　　　　　　　　　　　　様に云えるかどうかわからない。

　　　　　　　　　母平均値μについて、統計量（ｍ−μ）/（Ｓｔｄ/√（ｎ））の分布は、自由度ｄｆのｔ分布に従う事が知られ
　　　　　　　　ている。
　　　　　　　　　そうすると、次の不等式が成立する。
　　　　　　　　　　        　　−ｔ(α/2） ≦ （ｍ−μ）×Ｓｔｄ/√（ｎ）） ≦ ＋ｔ(α/2）
                                                      :
                                                      :　μについて不等式を解くと
                                                      :
　　　　　　　　　　　　　　　　　　　　　　　　　　　　↓
　　　　　　　　　　　　　　　　ｍ−ｔ(α/2）×Ｓｔｄ/√（ｎ） ≦ μ ≦ ｍ−ｔ(α/2）×Ｓｔｄ/√（ｎ）
　　　　　　　　　　　　　　　　　　　　　　　　　ｍ　　　　：　標本平均値
　　　　　　　　　　　　　　　　　　　　　　　　　ｎ　　　　：　標本数
　　　　　　　　　　　　　　　　　　　　　　　　　ｄｆ　　　：　自由度（＝ｎ−1）
　　　　　　　　　　　　　　　　　　　　　　　　　Ｓｔｄ　　：標本標準偏差
　　　　　　　　　　　　　　　　　　　　　　　　　α　　　　：　有意水準
　　　　　　　　　　　　　　　　　　　　　　　　　ｔ（α/2）：有意水準α、自由度ｄｆにおけるｔ分布表値

　　　　　　例１　ある集団の平均値を推定したい。集団から１６名をランダム抽出し、平均身長、標準偏差を計算すると、それぞ
　　　　　　　　れ１７０ｃｍ、１２ｃｍであった。
　　　　　　　　　このとき、信頼度９５％（有意水準５％）の場合で、元の集団全体の平均値（母平均値）を区間推定しなさい。

　　　　　　　解
　　　　　　　　　基本統計値
　　　　　　　　　--------------------
　　　　　　　　　　標本数　　　16
　　　　　　　　　　平均値　　　170
　　　　　　　　　　標準偏差　　12
　　　　　　　　　　有意水準　　0.05％
　　　　　　　　　--------------------
　　　　　　　計算
　　　　　　　　　　ｔ(0.05、16−1）の読取り値　＝　2.131　←-------　＝ｔｉｎｖ（0.05、16−1）
　　　　　　　　　　
　　　　　　　　　　従って、母平均値μは、163.6　〜　176.4
                                       =170−2.131×12/√(16)　〜  =170＋2.131×12/√(16)
　　　　　　　結論
　　　　　　　　　　信頼度９５％では、元の集団全体の身長の平均値は、１６３．６から１７６．４ｃｍと区間推定できる。

　　　　　例２　ある母集団からの標本２０名について、タンパク質摂取量（ｇ）を測定したところ、平均値が77ｇ、標準偏差は11ｇ
　　　　　　　であった。　
　　　　　　　１)この集団のタンパク質摂取量を信頼度95％で推定しなさい。
　　　　　　　２)この集団のタンパク質摂取量を有意水準1％で推定しなさい。　　　
　　　　　　解
　　　　　　　　　　基本統計値
　　　　　　　　　-------------------------------
　　　　　　　　　　標本数　　　　20
　　　　　　　　　　平均値　　　　77
　　　　　　　　　　標準偏差　　　11
　　　　　　　　　-------------------------------
　　　　　　　計算
　　　　　　　　１)
　　　　　　　　　　　　信頼度９５％におけるｔ分布表値
　　　　　　　　　　　　　　　ｔ(0.05,20−1）　＝　2.093024　　←--------------　＝ｔｉｎｖ（0.05、20−1）
　　　　　　　　　　　　従って、母平均値は、70.7　〜　83.3
　　　　　　　　　　　　　　　　　　　　　=77−2.093024×11/√(20)　〜  =77＋2.093024×11/√(20)
　　　　　　　　２)
　　　　　　　　　　　　有意水準１％におけるｔ分布表値
　　　　　　　　　　　　　　　ｔ(0.01,20−1）　＝　2.860935　　←--------------　＝ｔｉｎｖ（0.01、20−1）
　　　　　　　　　　　　従って、母平均値は、68.4　〜　85.6
　　　　　　　　　　　　　　　　　　　　　=77−2.093024×11/√(20)　〜　=77＋2.093024×11/√(20)

　　　　　　　結論
　　　　　　　　１)
　　　　　　　　　　信頼度９５％では、元の母集団のタンパク質摂取量の母平均値は、70.7から83.3ｇと区間推定できる。

　　　　　　　　２)
　　　　　　　　　　有意水準１％では、元の母集団のタンパク質摂取量の母平均値は、68.4から85.6ｇと区間推定できる。

　　　　　例３　ある地区で無作為に抽出した４０歳以上の男性の血清総コレステロール値は以下の通りであった。
　　　　　　　　この地区の４０歳以上の男性の血清総コレステロール値の母平均値は、どの範囲にあるか、信頼度９５％で区間推
　　　　　　　定しなさい。
　　　　　　　　　　　　　　データ（mg/dl）
　　　　　　　　　　　　-------------------------------------------------
　　　　　　　　　　　　　178　　190　　164　　170　　230　　190　　210　
　　　　　　　　　　　　　198　　240　　186　　170　　200
　　　　　　　　　　　　-------------------------------------------------
　　　　　　　解
　　　　　　　　計算
　　　　　　　　　　基本統計値
　　　　　　　　　-----------------------------
　　　　　　　　　　標本数　　　　　　12
　　　　　　　　　　平均値　　　　　　193.8
　　　　　　　　　　標準偏差　　　　　23.594
　　　　　　　　　-----------------------------
　　　　　　　　　　信頼度９５％におけるt分布表値
　　　　　　　　　　　　　　　t(0.05、12‐1)＝2.200985　←-------------------　＝ｔｉｎｖ（0.005、12‐1）
　　　　　　　　　　従って、母平均値は、187.2　〜　200.4
                                    =193.8−2.200895×23.594/√(12)　〜=193.8＋2.200895×23.594/√(12)　
　　　　　　　　結論　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　信頼度９５％では、この地区の４０歳以上の男性の血清総コレステロール値の母平均値は、187.2から200.4mg/dl
　　　　　　　　　と区間推定できる。