このプログラムの基礎方程式

定常状態のシュレディンガー方程式は



ただし、ハミルトニアン H は原子単位系では



となります。ここで Δ はラプラシアン、V はポテンシャル、 ψ は波動関数、E はエネルギーです。
ここで、ポテンシャル V を動径 r のみの関数



と近似し、波動関数 ψ を球座標系で動径 r ・経度 θ ・ 方位角 φ の関数に変数分離し



とします。動径波動関数を



と置き換えると、各成分の波動関数はそれぞれ







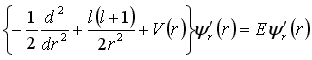
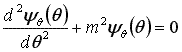
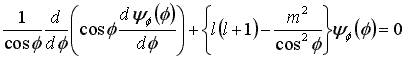
と書き表すことができます。 ここで l は角運動量量子数、 m は磁気量子数です。
この内経度及び方位角については解析的に解くことができて、解は





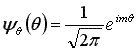
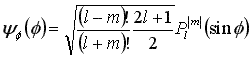
となります (ただし、P_l^m はルジャンドル陪多項式)。
動径については、ポテンシャルを



と分解してそれぞれ計算し、密度汎関数法で数値的に求めます。
ここで V_H はハートリーポテンシャル (電子の場によるポテンシャル)、 V_XC は交換・相関ポテンシャル、 Z は原子番号 = 電子の数 = 原子核の陽子の数で、 最後の項は原子核によるポテンシャルとなります。